
アインシュタイン(45歳)を救った、インドからの便り - その2
以下は昨年(2023年)10月24日に、勢いで書き綴ったブツです ⇩
その1とタイトルに付けながらその2がないことに先日検索で気づきました。そこで今回綴ってみようと愚考いたします。
たった4ページの論文が、アルくんを驚愕させました。インドからの英語論文です。アルベルトはそれをドイツ語にして、インドの無名物理学者ボースくんに代わって、ドイツのある科学誌に寄稿しました。
短いものなのでちゃちゃっと見ていきましょう。以下は一ページ目。何か数式がありますね。

拡大すると…プランクの式を使ったものですね。放射の密度と振動子の平均エネルギーとの関係式です。

「この式は、古典論からしか導出できない」とボースは論評します。古典論とあるのはおそらくウィーンの公式のことです。実際プランクはウィーン公式にインスパイアされています。
そのうえ上の式は、エーテル説を無意識に前提にしていて好ましくないと言いたげですボースくん。エーテルとは何かというと、アインシュタインが1905年に提唱し、やがて「相対論」と呼ばれることになる画期的理論によって存在が否定された、あのエーテル説のことよ鉄郎。

同じページの、二つ目の数式はどうでしょう。

ああっこれはアインシュタインの式です。1916年に、あるズルというか仮説を使って導出した、あれです。プランクの式、ボーアの式、ボルツマンの式をひとつにしてみせた、あの式ですよあの式。
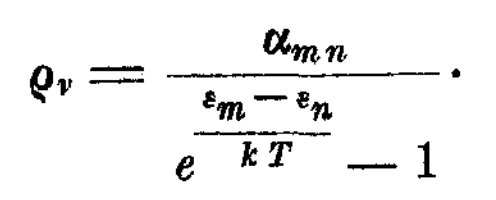
この式については以下で解説してあります。
ボースくん、アルのこの数式を高く評価しながら、導出において穴があることを指摘して…

以下は二ページ目。ボースくん、何やら計算を始めます。
放射が体積𝑉に封じ込められ、その総エネルギー𝐸が与えられているとする。異なる種類の量子がそれぞれの数 𝑠 とエネルギー𝜀で存在する(𝑠 は 0 から 𝑠 まで)。このとき総エネルギー𝐸は次のように表される。

拡大すると…

ここにある $${N_s}$$ とは、特定の状態または周波数範囲 𝑑𝜈 に存在する量子の数です。ボースくんそのあたりの説明は省いてるので私が補って説明しています。
ちなみにこの後 $${P_s}$$ なるものが登場します。確率を表します。特定の状態や範囲における量子の分布の確率です。
$${P_s = 総量子数/N_s}$$
ここからボースくん、相空間に議論のステージを移します。相空間とか何かというと、運動量 p と位置 q のペアこそが物理学の肝と考えて、それを二次元平面化したものです。pとqはそれぞれ三次元ですので相空間は六次元となります。
この空間を、エントロピーの考えに基づいて「細胞」に分割すると、エーテル説に頼らずとも、先ほどの式が導出できる・・・そう述べます。

(実はこの二年前にド・ブロイ様も、ウィーンの分布式を光量子説から導出できないかと頑張った際に、同じ技を使っています。「細胞」の体積を $${h^3}$$ と取って、ヘルムホルツ自由エネルギーを算出しています)
ボースくん、この「細胞」の各細胞についての分布確率を積分していくことで、最終的にプランクの公式にたどり着いてみせたのです。

論文最終ページの、ここ。

これにアインシュタインは超びっくり衝撃を受けました。1916年つまりボースより8年前、彼もこのプランク公式の導出に成功してはいましたが、一か所でズルをしていて、そのことを本人も論文中で吐露していました。⇩
ボースなる未知の人物が、とうとうズルなしで導出してみせたことに、アルくんは衝撃と感動を覚えました。ボースをインドからドイツ科学界に呼び寄せ迎え入れ、親交を結んだことからもそのことはうかがえます。
*
この論文のなかでボーくんは述べていないのですが、彼の計算は「光子にはアイデンティティがない」ことを示していました。
野球のボールが二つあって、マジックでそれぞれⒶとⒷと書き込めば、ⒶとⒷとして区別されます。アイデンティティが生じるわけです。しかし光子はこうならないのです。ボースの数式はそのことを示していました。
高校の数学で、確率論のイロハを皆さん習ってますよね。順列はPで、組み合わせはCで表わすのだと、習ったと思います。ボーくんの論文は(Cが表立っては使われていないけれど)Cで数式が組み立てられています。ということは組み合わせ、すなわち「野球の球が複数あって、どれを選ぼうがボールはボールだ」と、光子というボール(ボールは比喩です言うまでもなく)の特性を述べているのです。
このことをただちに悟ったアルくん、同1924年に気体分子について、さらに大胆な説を提唱し、論文を出しました。絶対零度に近づくと気体が粘性を持つという説です。ご本人はあまりこの研究を重要視しなかったようですが、私はこれもノーベル物理学賞授与に値する彼の研究のひとつだと考えます。
*
ああそれからさらに二年後の1926年に、ポール・ディラックが、アルの1916年論文(あるズルをしてプランク公式を導出したというアレ)中のアルのズルを、ボースとアインシュタインの1924年の研究+シュレディンガーの1926年の研究に刺激されて、ズルをズルではないものにしてみせています。
実はこちらを再論したかったのですよ。しかしその前に プランク➱アインシュタイン➱ボース➱アインシュタイン のバトンリレーについて再確認したかったので、今回のものを、思いつくまま綴ってみました。
つづくよきっと
