
エレン先生、フーリエ級数を小学生に教える
フーリエ級数というのがあります。数学です。こんなのです。
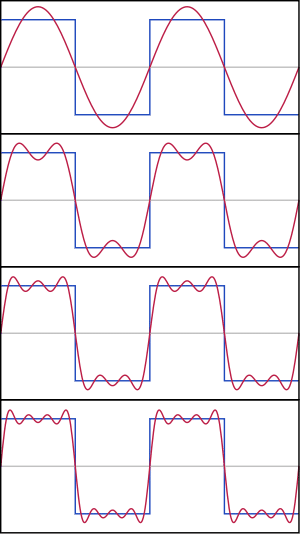
わかんない? そうですか。どんな形をした周波であっても、sinθ や cosθ などの素朴な三角関数の組み合わせで再現できてしまうというものです。たとえば、

三角形のでこぼこ波形であっても、いくつものシンプルな三角関数を組み合わせることで再現できます。こんなんでもです。

どんな周波でも sinθ や cosθ とそのお仲間を揃えれば再現できてしまう…それって証明できるの? ええできます。検索すれば証明法が出てきます。
ただ、検索してみたのですが「二進法」を使っての証明は見当たりませんね。
二進法とは、こんなのです。この表の左側が、私たちが普段使っている「10進法」の数。右側が「2進法」による数です。
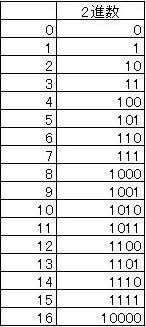
0と1の組み合わせをスイッチのオン/オフに置きかえてイメージしてください。

おっとなんだか波の形が浮かび上がってきたではありませんか。
ここで唐突ですが、てんびんの話に切り替わります。小学生のとき理科室で、こんな器具をいじったことはありませんか。

「てんびん」です。左のお皿にゴジラをのせて、右のお皿に分銅をだんだん載せていって、左右の傾きがなくなったとき、右のお皿にある分銅の重さ合計がゴジラの体重だよというの、皆さん実際にやったことがあると思います。
ここで問題です。ゴジラの体重が20~30グラムぐらいだとして、それを正確に測るためには、最低で何種類の分銅が要るでしょう?
「あ、こういうのなんか子どもの頃やったなあ」と思った方も少なくないと思います。答えを先に言うと、
1,2,4,8,16の5種類
です。1グラムの分銅を右の皿に載せても、ゴジラののっかった左の皿はびくともしません。2グラムの分銅を追加しても1+2=3グラムだからやはり変化はなし。4グラムの分銅を加えると7グラムに。さらに8グラムの分銅を加えると15グラム。えいっと16グラムの分銅を加えると…おっと右に傾いてしまいました。ゴジラは31グラムよりは軽いということです。
次に、右の皿から分銅をすべておろしてしまいましょう。そして今度は16グラムつまり最も重い分銅から右の皿にのっけていくのです。
16グラム
ゴジラのいる左の皿は動かない。そこで8グラムの分銅を右の皿にのっけてみると…
16+8=24グラム
おっとてんびんが右に傾いた! ゴジラは24グラムよりは軽いのです。
ここで8グラムの分銅を下ろして、代わりに4グラムの分銅を載せてあげましょう。
16+4=22グラム
おっと、ほぼ左右が平坦になった!しかしゴジラの載っている左側のほうがわずかに下にあるぞ。よし、右の皿に分銅を追加してみよう。2グラムのでどうだ?
22+2=24グラム
おっとっと今度は右の皿のほうがわずかに下になってしまったぞ。ならば2グラムの分銅を下ろして、代わりに1グラムのをのっけてみましょう。
22+1=23グラム
おお、今度はゴジラ(左側)と分銅たち(右側)がきれいに並んだ!
ということは、ゴジラの重さは23グラムということです。これは中学入試の算数問題で頻出もいいところなので、覚えておくといいことがあるかもしれませんね。
1,2,4,8,16の5種類
この組み合わせ、二進法で表してみましょう。
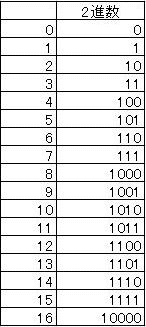
1,10,100,1000,10000
ピンとくる方もいらっしゃると思います。これらの二進法の値を組み合わせれば「11」でも「101」でも「10101」でも作れてしまうのです。
これね、こんな五種類でも同じことができます。
1 10 101 1010 10101
この五種類をうまく組み合わせれば「110」でも「11010」でも作り出せます。「110」が欲しければ「101」に「1」を足せばいいし、「11010」が欲しければ「10101」に「101」を足せばいいのです。
どうしてこの五種類でも同じことができてしまうのかというと…めんどくさいので説明は省略。「一対一対応になっているのだからこうなるに決まってら!」と雄たけびをあげて済ませておきましょう。
さてこの
1 10 101 1010 10101
って、こんな風にも見えてきませんか。
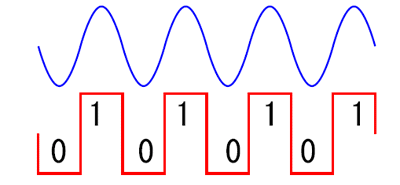
そうです波です。ごく素朴な波。もし同じ幅のなかに「1」や「10」や「101」や「1010」や「10101」らが押し込まれたとしたら、右のものほど細かく振動する波が脳裏に浮かびます。

「1」と「0」が交互に並ぶ数列いろいろを、いろいろ工夫して足し算すると、どんな「1」「0」の並び方でも再現できるというのなら、これら基本波の組み合わせで、どんな複雑怪奇な波形でも再現できないわけがない!
こんな風に考えれば、フーリエ級数はさっさと理解できてしまうのです。ちなみに
1 10 101 1010 10101
0 01 010 0101 01010
この二列の組み合わせでもOKです。上がコサイン波で下がサイン波に当たりますね。これをもっと数式として書きやすいものにアレンジすると、
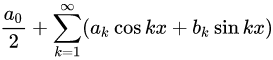
この有名な式になります。私がここまで説明した「1」「0」の組み合わせは、学習者の理解のためにあえて素朴なやり方で説明したものです。もっと解析的に波を扱う場合は、上の式のほうがいろいろ計算がラクになります。
[付記]「波の間隔ではなく幅が広がったり狭くなったりするのは『1』『0』の組み合わせで描けるわけ?」と思う方もいるでしょうが、描けます。二進法なのを多進法に換算して、一桁ごとに山あり谷ありの数列を思い描くのだと思い描ければ、難なく描けるとイメージできると思います。
