
やさしいドメモの論文 4 ~ランダムに宣言するモデル~
ランダムに宣言するモデル(ただし自分が宣言して外れだった数は除く)
このモデルはドメモで使用する数字である1から7をランダムに宣言します。
ただ、完全にランダムな宣言を行わせることにはほとんど意味がありません。通常のプレイヤーは外れだった数を再度宣言しないからです。
したがって次のように数字を宣言することになります。
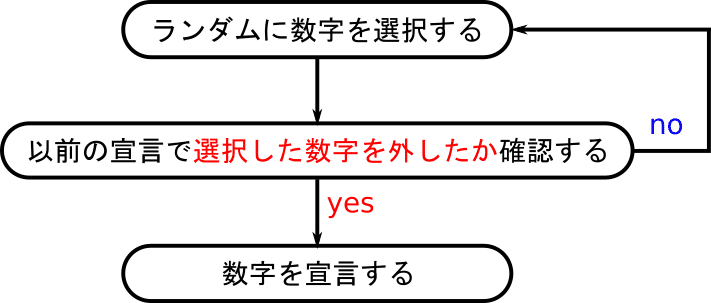
具体的には
4(ハズレ)ー>5(アタリ)ー>5(ハズレ)ー>これ以降は4と5を宣言しない
この実験は、ドメモのルールに則りつつ無茶苦茶な宣言をした場合にどのような結果へ落ち着くのかを見るために実施しました。
言い方を変えれば、下手だけど真面目なプレイヤーがプレイした場合、最大の宣言回数(最も悪い結果)はどうなるのか、を見つけたかったのです。
シミュレーションの結果を記載します。
条件は前回と同様です(ドメモを5人で10,000回プレイ)。

グラフから読み取れる点は以下のようになります。
右肩上がりのグラフになっている
最大宣言回数が10回である
右肩上がりのグラフになっている
ランダムに宣言するモデルの場合、最頻出する結果が最も悪い結果となっています。
宣言している数字はランダムに選ばれたものですから、プレイヤーの意思は介在していません。また、10,000回という実験回数によって、この結果が特定のゲームで発生するものではなく、多くのゲームに当てはまるなものだと言えます。
つまり、どれほどミスをしやすいプレイヤーでも、真面目にドメモをプレイしている限り、最頻出の宣言回数は10回となるわけです。
そして10回までで必ず全ての数字を当て終えます(これは次の節で)。
ここから言えることはブラフが他のプレイヤーへ与える影響度合いです。
どれほどミスをしやすいプレイヤーでも10回までで必ず数字を当て終えるわけですから、どれだけ巧みなブラフでも、4回(最小宣言回数)で終わるはずだったゲームを最大で10回に伸ばす効果しか得られません。
ブラフによって得られる最大の効果は、相手の勝利を6回遅らせることだとも言えます。
最大宣言回数が10回である
このモデルで行われる、具体的な数字の宣言を見てみます。
あえて、宣言回数が最大になるように試みているのですが、10回が限界に思えます。

最初に「5 6 7」を宣言します。これは自分の手札にはない数字ですからハズレとなり、次からは宣言できません。
(図中では、宣言できる数字から「5 6 7」が消えている)
残りは自分の手札にある数字ですから、1回目はアタリになります。2回目はハズレてしまい、宣言できなくなります。
これを繰り返すと、結局10個目に数字を宣言した段階で、手札にある数字を全て当て終えることになりました。
他の例でも当てはまるのか、一般化して考えましょう。
まずハズレた数字は宣言しないという、本モデルの方針を言い換えてみます。
論文から引用します。
これは自分の手札に、ある数 n が m 枚含まれている場合、その数 n は m + 1 回しか宣言することが出来ないと言える。
具体的に考えると、手札に数字の7が2枚あるとき、7は3回しか宣言できない、ということになります。
3回目の宣言は必ずハズレとなるため、4回目を宣言することはないわけですね。
nつまり数字は7種類で、mつまり枚数は最大で4枚です。
言葉だとわかりにくいので数式を活用すれば
m1+m2+m3+m4+m5+m6+m7=4
となります。
ここでm1からm7は自分が持っているある数nの枚数です。自分の手札は4枚しかないため、右辺は4になります。
例えば、1を1枚、3を2枚、7を1枚持っている場合は、
m1=1
m3=2
m7=1
それ以外は0になるため
m1 + m2 + m3 + m4 + m5 + m6 + m7 = m1 + m3 + m7 = 1 + 2 + 1 = 4
となります。
最初の議論に戻り、ある数nは自分が持っている枚数プラス1回宣言できるため、ゲーム中に自分が宣言する回数は以下のようになります。
(m1 + 1) + (m2 + 1) + (m3 + 1) + (m4 + 1) +
(m5 + 1) + (m6 + 1) + (m7 + 1)
=m1 + m2 + m3 + m4 + m5 + m6 + m7 + 7
m1 + m2 + m3 + m4 + m5 + m6 + m7 = 4だったため
m1 + m2 + m3 + m4 + m5 + m6 + m7 + 7 = 4 + 7 = 11
ゲームが終了したあとで数字を宣言する必要はありませんよね。
上の図で示したとおり、自分の手札にある数字が無くなった時点で宣言をやめるため、実際の宣言回数は1回少なくなります。
したがって、10回が最大宣言回数となるわけです。
