
やさしいドメモの論文 5 ~ 一般的なプレイヤーの思考モデル ~
一般的なプレイヤーの思考モデル
ここまで説明してきた以下のモデルたちは特殊です。
ドメモにおける公開情報を全く活用していませんでした。
一般的なプレイヤーは目隠しをしてこのゲームに参加しているわけではありません。
公開されている相手が持っているカードと場に置かれているカードの情報を見れます。

例として5人プレイの場合を考えてみます。この場合、使用しているカード28枚のうち、自分以外のプレイヤーが持っているカードは16枚、場で表になっているカードは4枚あります。
非公開となっているカードは場に伏せてある4枚と自分が持っているカード4枚です。
つまり、非公開情報は8枚だけしかありません。
この記事で考察する一般的なプレイヤーモデルは、この公開されている情報を参照して宣言する数字を絞り込みます。
例えば、相手が持っている3の枚数を合計して3枚あれば、自分が3を宣言する必要はないとわかるでしょう。
またランダムに宣言するモデルで導入したように、自分の宣言したカードがハズレだった場合も宣言しません。
思考の流れは以下のようになります。
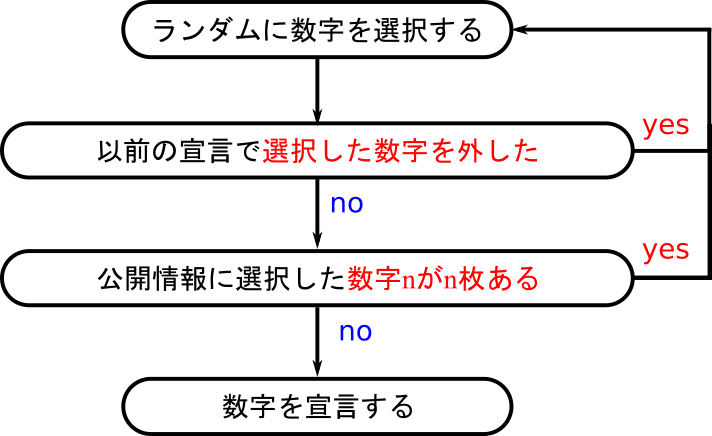
これまでの実験で行ってきた特殊なモデルと異なり、本モデルはかなり現実に即しています。
このモデルの結果は、プレイヤーがドメモで遊ぶ際の参考になると考え実験を行いました。
シミュレーションの結果を記載します。
条件は前回と同様です(ドメモを5人で10,000回プレイ)。

グラフから読み取れることとしては以下になります。
宣言回数が6回でゲーム回数のピークが現れている
最大宣言回数が8回である
宣言回数が6回でゲーム回数のピークが現れている
宣言回数6回というのは、最小宣言回数(4回)と最大宣言回数(8回)の中間です。
どうして最頻出回数が6回になるのか、という疑問は当然だと思うのですが、明確な回答は難しいです。
論文内でも特に言及しておりませんでした。
まず、このモデルもランダムに数字を選択していることに変わりはありません。したがって、この結果はプレイヤーの意図ではなく、プレイヤーモデルの意図を反映していると言えます。
次にランダムに宣言するモデルとの違いを考えると、これは公開情報を参照し活用している点だけになります。
当たり前ですが、この公開情報を参照するという行為が、ドメモにおいては重要なのです。
この行為によって、約35%(10,000回中3,500回程度)のゲームで宣言回数は6回となり、約30%(10,000回中3,000回程度)のゲームでは7回となります。
どうしてこのような結果になるのかについて考えることはとても面白いです。
ただ、ここでは結果に着目しました。ブラフを宣言することの価値です。
つまり、一般的なプレイヤーは6回で上がる確率が高いため、ブラフは1回までに留める必要があります。
最小宣言回数4回にブラフの1回を足して5回となります。
6回で上がるプレイヤーに勝つには、1回までしかブラフを宣言できないのです。
最大宣言回数が8回である
これは非公開となっているカード枚数が8枚であることを表しています。
真面目に宣言を行えば、どんな手札でも8回以内で上がることができます。
