【統計力学１０】量子力学的な粒子の統計【ボーズ分布とフェルミ分布】

前回は，調和振動子を正準交換関係を満たすような位置と運動量を用いて量子力学的に扱うと，振幅の取りうる値は離散的な値に限られることを見ました．一つの調和振動子の場合は，このことは単にエネルギー準位がとびとびの値をとることを意味します．電磁場に対してはどうだったでしょう．古典電磁気学によると，電磁場はある波数をもった波動のそれぞれについてが調和振動子と同等に扱えます．それぞれの波数でラベルされた「調和振動子」について，振幅，すなわちエネルギーの値が量子化され，全エネルギーは

$$
E = \sum_k n_k \hbar \omega_k
$$

で与えられます．ここで，添え字は波数によって調和振動子のそれぞれをラベルしたことを意味します．そして，このときの量子状態は，各調和振動子の「エネルギー量子数」

$$
n_1, n_2,\ldots
$$

を指定すれば決まることになります．エネルギー量子数とは，前回導入した次の演算子（これらを生成消滅演算子といいますが，今回はこの演算子の意味については立ち入りません）

$$
a_k = \sqrt{ \frac{m\omega}{2\hbar} } q_k + \frac{i}{\sqrt{2m\hbar \omega}} p_k,\\
a_k^{\dagger} = \sqrt{ \frac{m\omega}{2\hbar} } q_k - \frac{i}{\sqrt{2m\hbar \omega}} p_k
$$

によって定義される数演算子

$$
a_k^\dagger a_k = n_k
$$

の固有値のことです．ただしここではこれらも波数でラベルしました．

これを粒子的な見方をすると，ある波数をもった電磁波はエネルギー

$$
\epsilon_k = \hbar \omega_k
$$

をもった粒と考えるのですから，全エネルギーの式と比較すると，先の式でエネルギー量子数といったものは，あるエネルギーをもった粒（光子）の数だと考えられることになります．このことを「エネルギー準位の占有数」と表現することがあります．ところで，今粒子的な見方をするといいましたが，どの粒子がどのエネルギーを持っているのかということは一切考えていません．常識的な粒子であれば，量子状態はエネルギー量子数の組を指定するだけでなく，「どの粒子がそのエネルギーに属するのか」というところまで決めなければ状態は完全には決まらないように思われます．しかし，このまま数だけを指定するのが正しくプランクの公式を導くわけです．つまり，量子力学では本質的に粒子は区別しないということになります．この性質を不可弁別性（indistinguishable）といいます．例えるなら，電光掲示板上で光っている点を区別することに意味はないことに似ています．

（波動関数というものを知っている人のための注：位置で表示された波動関数に対して，不可弁別性を課すためには，波動関数を対称化または反対称化して制限してやることが必要になります．対して，生成消滅演算子を用いた方法ではすでに不可弁別性が自然に入っているという点で優れています．これは，単にエネルギー量子数で決まるようなより抽象的な「状態」を考えることで，粒子の位置というような部分系に分けられる実在論的な量に落とし込まずに扱えているからです．量子力学は本質的に実在論ではなく，各部分がもつれあっていて全体として一つの状態と考えなければならない場合も扱える理論なのです．ちなみに生成消滅演算子を使った量子化の方法を第二量子化と呼ぶことがありますが，何かを二回量子化しているわけではなく，単に昔の混乱した呼び名の名残であって，波動関数を対称化または反対称化する方法と等価です．）

数演算子の固有値は

$$
n_k = 0,1,2,\ldots
$$

となります．このように，あるエネルギーの粒子の数がいくらでも増えることができるような性質をもった粒子のことをボーズ粒子（Boson）といいます．光子はボーズ粒子の例です．

自然界にはボーズ粒子だけでなく，あるエネルギーの粒子の数が

$$
n_k = 0, 1
$$

の二通りしかとらないような粒子があることが知られています．このような性質を持った粒子のことをフェルミ（Fermi）粒子といいます．電子はフェルミ粒子です．固有値がこの二通りにしかならないという状況は，これまでと同様に考えてもでてきませんが，生成消滅演算子の交換関係に

$$
a_k^{\dagger} a_{k} + a_{k} a_k^{\dagger} = 1
$$

のような関係（反交換関係といいます）を課してやるとこのときの数演算子の固有値は０または１の二通りとなることが示せます．このときの一般化座標や運動量といった正準変数はもはや正準交換関係を満たしていませんが，調和振動子の運動方程式を満たすようにハミルトニアンを考えることは一応できて，これでフェルミ粒子を良く記述することができます．量子力学においては，正準交換関係は別に原理ではなくて，同じ運動方程式を満たすように別の交換関係を満たす演算子をとっても，それは一応量子的な変数としての資格があるということになります．とはいえ，物理的な意味があるものは限られています．

量子力学的な粒子系の統計力学

前回はプランク分布というものを導出しましたが，これは粒子がいくらでも生まれることができるので全粒子数一定という制限がない場合のボーズ粒子の分布であるといえます．今度は，粒子の生成消滅が起こらず，全粒子数が一定に保たれるような物質粒子の場合を考えてみましょう．

粒子間に相互作用がないときに話を限ります．このときの量子力学的な状態は各エネルギー準位を占める粒子数で指定され，そのカノニカル分布は

$$
f(n_1,n_2,\ldots) = \frac{e^{-\beta \sum_k \epsilon_k n_k}}{Z(\beta,N)}
$$

であり，分配関数は（積分ではなく和で）

$$
Z(\beta,N) = \sum_{\sum n_k = N} e^{-\beta \sum_k \epsilon_k n_k}
$$

となります．ここで，和は

$$
\sum_k n_k = N
$$

という全粒子数一定という制限をつけたうえで，あらゆる許される状態について足し上げることをしなければならないわけですが，この制限のせいで計算が困難です．

そこで，ミクロカノニカル分布からカノニカル分布に移ったときの事情を思い出してみます．ミクロカノニカル分布は全エネルギー一定という制限を付けた和を考えるのでやっかいだったのが，カノニカル分布ではエネルギーの代わりに温度を指定することにより，エネルギーのほうはぼかしてしまっていくらでも増やして和をとってもよくなりました．これによって計算がしやすくなるのでしたが，数学的には状態密度のラプラス変換が分配関数になっていることによります（こちらを参照）．

というわけで，分配関数を粒子数についてラプラス変換した

$$
\Xi(\beta,\alpha) = \sum_N^{\infty} e^{-\alpha N} Z(\beta,N)
$$

という関数を考えます．この関数を大分配関数（grand partition function）と呼びます．ラプラス変換の物理的意味を見るために，大分配関数を

$$
\begin{align*}
\Xi(\beta,\alpha) &= \sum_N^{\infty} e^{\ln Z(\beta,N) -\alpha N} \\
&= \sum_N^{\infty} e^{-\beta(F(\beta,N) - \mu N)}
\end{align*}
$$

と変形します．ここで，統計力学の基本公式を用い，また

$$
\mu = -\frac{\alpha}{\beta}
$$

と置きました．指数の肩の関数のオーダーはやはり

$$
F(\beta,N) - \mu N = O(N)
$$

なので，この指数関数は，例によって，あるピークを与えるような粒子数から少し外れるだけで急激に小さくなります．すなわち，最大項によって和を置き換えて

$$
\Xi(\beta,\mu) \approx e^{-\beta(F - \mu N)}
$$

としてよいことになります．ただし，このときの粒子数は

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\pd{F}{N} = \mu
$$

を満たすような粒子数として定まります．平衡状態を記述するためには，このときの粒子数が，平衡状態の粒子数と一致していなければなりません．平衡状態において，自由エネルギーの粒子数での微分係数は，化学ポテンシャルだったことを思い出すと，ラプラス変換の変数で定義した

$$
\mu = -\frac{\alpha}{\beta}
$$

は化学ポテンシャルを表していることがわかります．

平衡状態での分布であるカノニカル分布を変形して

$$
\begin{align*}
f(n_1,n_2,\ldots) = \frac{e^{-\beta \sum_k \epsilon_k n_k}}{Z(\beta,N)}\\
= \frac{e^{-\beta \sum_k \epsilon_k n_k}}{e^{-\beta F}}\\
= \frac{e^{-\beta \sum_k (\epsilon_k - \mu) n_k}}{e^{-\beta (F - \mu N)}}\\
\approx \frac{e^{-\beta \sum_k (\epsilon_k - \mu) n_k}}{\Xi(\beta,\mu)}
\end{align*}
$$

と大分配関数を規格化定数とした形に書きなおすこともできます．この確率分布モデルをグランドカノニカル分布といいます．グランドカノニカル分布は，温度と化学ポテンシャルによってマクロな系の状態を指定したときに平衡状態を記述する分布だといえます．（よって，カノニカル分布を導くときにやったように，系がエネルギーおよび粒子を環境とやりとりしているような状況を考えて，そこに典型性を課してやっても導くことができます．しかしここでは，平衡状態においてはカノニカル分布とグランドカノニカル分布が等価であることが素直にわかるように議論しました．設定によって計算のしやすさが異なるのでうまく変数をとりましょう，ということになります．）

さて大分配関数は物質粒子について，分配関数をラプラス変換した

$$
\begin{align*}
\Xi(\beta,\mu) &= \sum_N^{\infty} e^{\beta\mu N} \sum_{\sum n_k = N} e^{-\beta \sum_k \epsilon_k n_k} \\
&= \sum_{N}^{\infty} \sum_{\sum n_k = N} e^{\sum_k - \beta( \epsilon_k - \mu) n_k}
\end{align*}
$$

となります．ここまで変形すると，粒子数に関する和があるおかげで全粒子数一定の制限がはずれてくれて，各エネルギー準位を占める粒子数について勝手に和をとることができて

$$
\begin{align*}
\Xi(\beta,\mu) &= \sum_{n_1}\sum_{n_2}\cdots e^{\sum_k - \beta( \epsilon_k - \mu) n_k}\\
&= \prod_{k} \sum_{n} e^{ -\beta( \epsilon_k - \mu )n}
\end{align*}
$$

とできます．式を眺めると，各エネルギー準位について独立に，新しくエネルギーの基準を化学ポテンシャルにずらして測った

$$
( \epsilon_k - \mu) n
$$

というエネルギーでもってカノニカル分布を考えたときの分配関数になっています．化学ポテンシャルからエネルギー準位を測ってやれば，各エネルギー準位について独立に粒子が出入りしているというイメージをもって問題なくなるのです．したがって，大分配関数を用いて，ある量子状態に系を見出す確率は，

$$
f(n_1,n_2,\ldots) = \frac{\prod_k e^{-\beta(\epsilon_k - \mu)n_k}}{\Xi(\beta,\mu)}
$$

または，あるエネルギー準位にある粒子数で粒子が入っている確率として

$$
f(n_k) = \frac{e^{-\beta(\epsilon_k - \mu)n_k}}{\xi(\beta,\mu)}
$$

という分布で記述できます．ただし

$$
\xi(\beta,\mu) = \sum_{n} e^{ - \beta( \epsilon_k - \beta)n}
$$

はある一つのエネルギー準位についての大分配関数として定義しました．

ボーズ粒子の場合，各エネルギー準位に入る粒子数としてすべての自然数をとることが許されるので，

$$
\sum_{n_k} e^{ - \beta( \epsilon_k - \mu)n_k} = \sum_{n_k =0}^{\infty} e^{ - \beta (\epsilon_k - \mu)n_k} = \frac{1}{1 - e^{-\beta (\epsilon_k - \mu)}}
$$

となります．一方，フェルミ粒子の場合，各エネルギー準位に入る粒子数として０または１のみが許されるので，

$$
\sum_{n_k} e^{ - \beta (\epsilon_k - \mu)n_k} = \sum_{n_k =0,1} e^{ - \beta( \epsilon_k - \mu)n_k} = 1 + e^{-\beta (\epsilon_k - \mu)}
$$

となります．以上をまとめて，大分配関数の計算結果は

$$
\Xi(\beta,\mu) = \prod_k (1 \mp e^{ - \beta (\epsilon_k - \mu)})^{\mp 1}
$$

と書くことができます．（ここで複号の上がボーズ粒子，下がフェルミ粒子を表すと約束しておきます．）

ここから，各エネルギー準位に占める粒子数の期待値を計算してみると，

$$
\newcommand{\alr}[1]{\left\langle #1 \right\rangle}
\alr{n_k} = \sum_k n_k f(n_k) = \frac{1}{e^{\beta(\epsilon_k - \mu)} \mp 1}
$$

となります．これらをそれぞれ，ボーズ分布，フェルミ分布といい，図のような分布になっています．

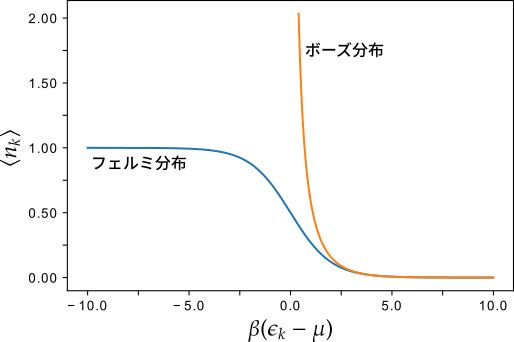
化学ポテンシャルは，全粒子数が一定という条件

$$
\newcommand{\alr}[1]{\left\langle #1 \right\rangle}
N = \sum_k \alr{n_k} = \sum_k \frac{1}{e^{\beta(\epsilon_k - \mu)} \mp 1}
$$

によって決まります．

ボルツマン分布

ボーズ分布，フェルミ分布においてもし

$$
e^{\beta(\epsilon_k - \mu)} \gg 1
$$

がすべてのエネルギー準位について成り立つなら，ボーズ分布とフェルミ分布の違いは効かなくなって，

$$
\newcommand{\alr}[1]{\left\langle #1 \right\rangle}
\alr{n_k} = e^{-\beta(\epsilon_k - \mu)}
$$

と書かれることになります．こうして近似された分布をボルツマン分布といいます．ボルツマン分布は，ボーズ粒子とフェルミ粒子の違いという量子力学的な効果が表れない，古典近似です．

この近似が成り立つ条件を考えてみましょう．ボルツマン分布を使って全粒子数を考えると

$$
N = \sum_k e^{-\beta(\epsilon_k - \mu)}
$$

で，この和を古典的に扱うと

$$
\begin{align*}
N &= \frac{V}{h^3} \int dp\ e^{-\beta {p^2}/(2m)} e^{\beta\mu}\\
&= e^{\beta \mu} \frac{V (2\pi m kT)^{3/2}}{h}
\end{align*}
$$

となります．すべてのエネルギー準位（これは非負）に対して，

$$
e^{\beta(\epsilon_k - \mu)} \gg 1
$$

の条件が成り立つためには，

$$
\newcommand{\lr}[1]{\left(#1\right)}
\lr{\frac{V}{N}}^{\frac{1}{3}} \gg \frac{h}{\sqrt{2\pi m kT}}
$$

が必要となります．左辺は粒子間の平均的な距離を表しています．右辺は，その温度での量子力学的なゆらぎの大きさの指標であり，熱的ド・ブロイ（de Broglie）波長と呼ばれます．高温かつ低密度な条件の下では，熱的ド・ブロイ波長は粒子間の平均距離に比べて無視できるようになり，ボルツマン分布の近似がよい精度で成り立つことがわかります．また，化学ポテンシャルはこのとき負の値を持ち，温度の増加に伴って小さくなる量であるとわかります．

今回のまとめ

量子力学では同種粒子は区別しない．相互作用がなければ，エネルギー準位をいくつの粒子が占めているかだけで量子状態は指定される．エネルギー準位の占有数の期待値の分布を調べるためには，グランドカノニカル分布を導入するのが便利で，それを用いてボーズ粒子とフェルミ粒子に対する分布を得た．その古典近似はボルツマン分布という．

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
更新履歴
Aug. 6 2023 第二量子化に関する注をより詳しく加筆