【統計力学１】位相空間における力学の形式【力学的な状態と運動】

ちょっと堅苦しいタイトルになってしまいましたが，これからやりたい統計力学の準備として，ミクロな力学が従うと考えられている法則をまずは考えておきましょう．

しばらくは古典力学の範囲で説明したいと思います．何でもかんでも量子力学を持ち出さずに既存の理論を工夫して，どこまで説明できるかを見ることは，逆に量子力学の本質を知るために重要なことだと思います．また，古典力学で考えることにも理論的な美しさがあると私は思います．

以下では解析力学の知識を少々天下り的に与えます．もし今回の話がわからなくても統計力学の計算はできるようになりますので，あまり実用面では今回の話を心配する必要はないと思われます．

それでは始めましょう．

位相空間

古典力学で運動を一般的に扱うには，ハミルトン（Hamilton）の正準形式が便利です．この力学の形式では，ある自由度$${f}$$の力学系に対して，一般化された座標$${q_i}$$と一般化された運動量$${p_i}$$の組

$$
\begin{align*}
(q_1,q_2,\ldots,q_f,p_1,p_2,\ldots,p_f)
\end{align*}
$$

によって状態を指定します．この状態空間のことを位相空間（phase space）と呼びます．任意の物理量は，位相空間上の関数として表されます．以下では一般化座標と一般化運動量のことを単に座標と運動量と呼ぶことにします．

自由度はマクロな系では，たとえば流体なら，粒子の数の3倍（3次元空間なので）になるので，これは普通は莫大な自由度を持っています．

（注: 数学でも位相空間という言葉がありますが，まったく関係ありません．数学の位相空間は英語ではtopological spaceなのに，なぜか同じ訳語になっています．）

運動方程式とその解

位相空間上の代表点が状態を表しますが，その点の時間変化によって運動を表します．その運動は次の正準方程式（canonical equation）と呼ばれる美しい方程式

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\begin{align*}
\dot{p}_i &= - \pd{H}{q_i}\\
\dot{q}_i &= \pd{H}{p_i}
\end{align*}
$$

によって決まります．ここで，$${H}$$はハミルトニアンと呼ばれ，系全体のエネルギーを，座標と運動量とで表したものです．

運動方程式の解として，運動の描く軌跡（トラジェクトリ）が求まります．トラジェクトリは位相空間上で交わることはありません．運動は一つに決まるはずだからです．したがって，トラジェクトリは無限に続くか，閉曲線となります．また，エネルギー保存則から，トラジェクトリは位相空間内の，エネルギーの等しい部分の集合（等エネルギー面）の上に描かれるはずです．（面といっても多次元の面です！普通は絵に描けません．）

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

例: 調和振動子のトラジェクトリ

ばねに繋がれた粒子を理想化したものを調和振動子といいます．質量$${m}$$，固有振動数$${\omega_0}$$の調和振動子のハミルトニアンは

$$
\begin{align*}
H = \frac{p^2}{2m} + \frac{m\omega_0^2 q^2}{2}
\end{align*}
$$

で与えられます．これに基づいて運動方程式を解くと

$$
\begin{align*}
q &= A\sin(\omega_0 t +\phi)\
p &= m\omega_0 A\cos(\omega_0 t +\phi)
\end{align*}
$$

となります．二つのパラメータはそれぞれ$${A}$$は振幅，$${\phi}$$は初期位相とと呼ばれ，初期条件によって決まる量です．対応するエネルギーは

$$
\begin{align*}
E = \frac{p^2}{2m} + \frac{m\omega_0^2 q^2}{2} = \frac{1}{2} m\omega_0^2 A^2
\end{align*}
$$

となり，振幅の二乗に比例した形となります．

トラジェクトリは次の図のような楕円になっています．この場合，等エネルギー面（二次元なので面といっても線になっています）をくまなく運動していることがわかります．

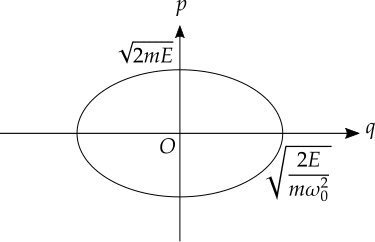
また，楕円の面積はエネルギーに比例していることにも注目しておきましょう．

たくさんの調和振動子の運動を考えてみることもできます．この運動は多次元の位相空間の上に表されます．２つの調和振動子を考えるだけでも，位相空間の次元は４次元になります．先ほどのようにトラジェクトリの絵を描くことはできません．

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

リウビルの定理

統計力学では，個々のトラジェクトリを考えるのではなく，たくさんの異なる代表点の集まりを同時に考える，ということをします．このとき，代表点の分布に着目して，分布が運動に伴って時間変化するのだという見方ができます．

分布とは，位相空間内のある点の近くに代表点が見いだされる確率密度によって表されます．時間$${t}$$において，点$${(q,p)}$$の近くに代表点が見いだされる確率密度は，位相空間上の関数として$${f(q,p,t)}$$と表記されます．

確率の和は保存しますから，連続の式と呼ばれる次の式

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\Div}{\mathrm{div},}
\begin{align*}
\pd{f(q,p,t)}{t} = -\Div(f(q,p,t)\bm{v})
\end{align*}
$$

が成り立ちます．ここで，

$$
\begin{align*}
\bm{v}(q,p,t) = \begin{pmatrix}
\dot{q}\\
\dot{p}
\end{pmatrix}
\end{align*}
$$

は代表点の作る速度場です．連続の式は，ある点に注目したときに，「その点でのある量の分布の時間変化」は，「時間当たりに周りから流れ込んでくる量」に等しいという，当たり前のことを表現しています．（当たり前の関係なのでこれだけでは物理法則ではありません．）

連続の式の右辺に，正準方程式を代入して計算を進めると，

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\lr}[1]{\left(#1\right)}
\newcommand{\Div}{\mathrm{div},}
\newcommand{\ppdd}[3]{\frac{\partial^2 #1 }{\partial #2 \partial #3 }}
\begin{align*}
-\Div (f(q,p,t)\bm{v}) &= - \sum\lr{\pd{f}{q}\pd{H}{p} - \pd{f}{p} \pd{H}{q} - f \ppdd{H}{q}{p} + f \ppdd{H}{p}{q}}\\
&= \sum\lr{\pd{f}{p}\pd{H}{q} - \pd{f}{q}\pd{H}{p}}
\end{align*}
$$

が得られるので，分布関数の時間発展の基本方程式は，

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
\pd{f(q,p,t)}{t} = \sum\lr{\pd{H}{q}\pd{}{p} - \pd{H}{p}\pd{}{q}} f(q,p,t)
\end{align*}
$$

となることがわかります．これをリウビル（Liouville）方程式といいます．シンプルに表記するために，

$$
\newcommand{\lr}[1]{\left(#1\right)}
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\cL}{\mathcal{L}}
\begin{align*}
\mathcal{L} = \sum\lr{\pd{H}{q}\pd{}{p} - \pd{H}{p}\pd{}{q}}
\end{align*}
$$

というリウビリアンと呼ばれる演算子を定義して，

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\cL}{\mathcal{L}}
\begin{align*}
\pd{f(q,p,t)}{t} = \cL f(q,p,t)
\end{align*}
$$

と書くこともあります．

繰り返しになりますが，今の議論は，位相空間を上から眺めたときに，確率分布がどのように運動するのか，というお話です．一方で，その運動に一緒についていきながら，分布の変化を眺めるとどうでしょうか？そのためには，分布関数の時間での全微分をとればよく（こうすれば座標や運動量にも時間微分がかかります），これは計算すると

$$
\newcommand{\lr}[1]{\left(#1\right)}
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\newcommand{\cL}{\mathcal{L}}
\begin{align*}
\frac{df}{dt} &= \pd{f}{t} + \sum\lr{\pd{f}{p} \dot{p} + \pd{f}{q} \dot{q}}\\
&= \pd{f}{t} - \cL f\\
&= 0
\end{align*}
$$

とゼロになります．つまり，代表点を追跡すれば，代表点の密度は時間がたっても変化しないことを意味しています．位相空間内で代表点の集合の作る体積は運動によって変化しないと言い換えることもできます．これをリウビルの定理といいます．

代表点が一様に分布しているなら，状態の数を数えるために，位相空間の体積で測ることができる，ということがリウビルの定理があるおかげでいえます．統計力学では，状態の数を数えることが重要になるので，今回この定理を紹介したのです．

ミクロ状態とマクロ状態の違い

ミクロに見た状態は，正準方程式に従って時々刻々と変化しています．これは永久に緩和することはなさそうです．しかも莫大な自由度を持っています．

一方で，マクロに見た状態は，平衡状態に落ち着き，時間変化しなくなります．そしてその状態は，温度や体積や粒子数といったわずかな自由度だけで（熱力学の状態空間上で）指定することができます．

というわけで，疑問が二つ出てきます．一つは，なぜミクロ状態は時間変化し続けるのに，マクロには緩和が起こり，平衡状態にとどまり続けるのか．もう一つは，なぜミクロの莫大な自由度がマクロのわずかな自由度に対応するのか．この二点にいかに答えるか，を次回のテーマとします．

今回のまとめ

・座標と運動量を組とする空間は位相空間と呼ばれ，位相空間上の一点を代表点という．
・ミクロな状態は代表点によって完全に指定され，運動はその軌跡（トラジェクトリ）で表される．
・位相空間内での代表点の集合の体積は，運動によって変化しない．（リウビルの定理．）
・位相空間と熱力学の状態空間がどのように対応するのかが，統計力学を考える上で問題となる．

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

更新履歴
May 21, 2020 調和振動子のトラジェクトリの図中の式の間違いを修正