【統計力学４】温度の統計力学的な定義【開放系でのエネルギーのつり合い】

ミクロな力学を記述する法則は基本的に孤立系についての法則です．しかし，普通は完全に孤立した系というのはありません．そのため，孤立系を考え，エネルギーで状態を指定する方法はあまり自然ではありません．

孤立系から開放系に移行するために，二つの孤立系（着目系と環境）を熱的にくっつけてやるという手続きを踏みます．

熱力学でもそのように考えることで，着目系と環境とでエネルギーをやり取りした結果同じ値になるものとして，温度を導入することができました．同じように着目系と環境とを接触させたような系を考えて，温度を導入することができます．

最確分布を与えるエネルギーの分配

まず，全系のエネルギー$${E^{\mathrm{tot}}}$$は，着目系のエネルギー$${E}$$と環境のエネルギー$${E^\mathrm{B}}$$の和として書けて，

$$
\newcommand{\tot}{\mathrm{tot}}
\newcommand{\Bth}{\mathrm{B}}
E^{\tot} = E + E^{\Bth}
$$

であるとします．ここで着目系と環境の間の相互作用エネルギーを無視しています．もちろん，状態が平衡状態に達するには，相互作用がいるのですが，平衡状態に達した後のことを計算できるようにするのが目標なので，この近似が許されます．

着目系があるエネルギー$${E}$$を持った状態になる確率$${f(E)}$$は，そのときの着目系の状態数$${\Omega_0(E)}$$と，環境の状態数$${\Omega^\mathrm{B}}$$の両方に比例します（つまり着目系と環境とを同時に考えたときの場合の数に比例します）から，次のように書けます:

$$
\newcommand{\tot}{\mathrm{tot}}
\newcommand{\Bth}{\mathrm{B}}
f(E) \propto \Omega_0(E) \Omega_0^{\Bth}(E^{\tot} -E)
$$

平衡状態では，着目系と環境との間でエネルギーを分配しあって，ちょうどいいところで落ち着きます．そして経験が教えるように，系のサイズが十分大きければ，平衡値の周りでのゆらぎは無視できるほど小さくなります．したがって，確率の分布は，エネルギーの平衡値のところに鋭いピークを持っているはずです．これは状態数がエネルギーに関する猛烈な増加関数であるなら，次の図のようになって，満たされます．

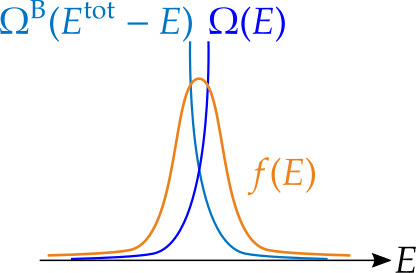
前回見た例では，状態数に$${E^N}$$というような項が含まれていたので，確かにエネルギーに関する猛烈な増加関数になります．

それでは，このピークを与えるエネルギーの値を求めましょう．対数をとると積が和に分解できるので条件が求めやすくなります．そして極大値では微分係数がゼロになることを条件とすればいいわけですから，結局，

$$
\newcommand{\tot}{\mathrm{tot}}
\newcommand{\Bth}{\mathrm{B}}
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\begin{align*}
&\pd{\ln\Omega_0(E)}{E} + \pd{\ln \Omega_0^{\Bth}(E^{\tot} - E)}{E} =0\\
&\therefore \pd{\ln\Omega_0(E)}{E} = \pd{\ln \Omega_0^{\Bth}(E^{\Bth})}{E^{\Bth} }
\end{align*}
$$

を満たすようなエネルギーが，確率を最大にするエネルギーの値です．

ここで，系に固有の今のところ謎の関数

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\beta(E) = \pd{\ln \Omega_0(E)}{E}
$$

が得られ，しかも平衡状態ではその値が接触している系との間で等しくなるようなものが得られました．これは熱力学第零法則から温度を導いたときの状況に似ています．そこで，これは熱力学で定義した温度に対応する関数に違いないと考えられます．しかし，まだどのように対応するのかは自明ではありません．

理想気体について

もう少し詳しく調べてみるために，理想気体を考えてみます．理想気体の状態数は

$$
\newcommand{\lr}[1]{\left(#1\right)}
\Omega(E) \approx \text{（定数）}^N \times \lr{\frac{V}{N}}^N \lr{\frac{E}{N}}^{3N/2}
$$

と与えられましたから，これをもとに先の謎の関数を計算してみると，

$$
\beta(E) \sim \frac{3}{2} \frac{N}{E}
$$

が得られます．

ところで，単原子気体の理想気体のエネルギーと温度の関係（状態方程式の一種）は，

$$
E = \frac{3}{2} N kT
$$

となることが実験的に知られています．ここで出てきた定数は，ボルツマン（Boltzmann）定数と呼ばれ，

$$
k = 1.380649 \times 10^{-23} \mathrm{J}/\mathrm{K}
$$

このような値（2019年から定義値になりました）を持つ定数です．

（注: 状態方程式の具体的な形は熱力学の理論枠組みから出せるものではなく，実験的に決めるものです．熱力学の役割は，系の特定の性質によらない普遍的な原理を与えることであって，具体的な系の特徴を反映した状態方程式を与えることはできません．ただし，いったん統計力学の枠組みが完成しさえすれば，ミクロなモデルを仮定することによって，統計力学から様々な系の状態方程式を求めることができるようになるのです．熱力学と統計力学は互いに支えあっています．）

この状態方程式を先の関係に代入すれば，

$$
\beta(E) \sim \frac{1}{kT}
$$

が得られます．こうして，謎の関数は逆温度に対応しそうであることがわかりました．

一般化

温度とは，物質の種類によらず，熱的に接触していて平衡状態にある系ではある決まった値を持つものですから，この関係は理想気体に限らず普遍的なものであるべきです．

以上の考察を経て，熱力学と統計力学を関係づける次の要請を入れます．

要請２（統計力学的温度と熱力学的温度の一致）
熱力学的な温度が，状態数と次の式で関係づいている．

$$
\newcommand{\pd}[2]{\frac{\partial #1 }{\partial #2 }}
\begin{align*}
\frac{1}{kT} \sim \pd{(\ln \Omega_0(E))}{E}
\end{align*}
$$

こうして，ボルツマン定数は，ミクロな物理量である状態数とマクロな物理量である温度とを橋渡しする定数として現れます．ボルツマン定数は統計力学を象徴する定数だと言えるでしょう．

平衡統計力学の要請は，基本的に「典型性」と「統計力学的温度と熱力学的温度の一致」の二つだけです．

今回のまとめ

・着目系と環境を熱的に接触させた系を考えることによって，温度を導入でき，状態数から導かれる統計力学的な温度が，熱力学的な温度と対応することを要請する．