偏微分方程式の数値解析①【陽解法と陰解法とクランク・ニコルソン法】

偏微分方程式は物理の問題でよく出てきますが，それが解析的に解けるというのはそう多くありません．しかし，微分方程式というのは時間や空間をわずかに変化させたときに物理量がどのように変化するかを表した数式ですから，少しずつ時空間のステップを刻んでちまちまと計算すれば積分した結果を近似的には知ることはできるはずです．これを手計算でやるのは途方もないので，計算機にやらせようというのが「数値的に微分方程式を解く」ということです．

偏微分方程式の離散化

本稿では例としてフォッカー・プランク方程式

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\pd{}{t} f(x,t) = - \pd{}{x} A(x,t) f(x,t) + \frac{1}{2}\ppd{}{x} B(x,t) f(x,t)
$$

を取り上げて，この数値計算法を考えます．（フォッカー・プランク方程式についてはこちら．）

まず，ステップバイステップで数値を求めることができるようにするために，連続な変数で書かれたこの式を離散的な変数で書き換える必要があります．
左辺の時間微分については前進差分という差分

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{f(x,t)}{t} \to \frac{f_i^{n+1} - f_i^n}{ \Delta t}
$$

に置き換えて微分を近似します．（ここでは，短く表記するために，下付き添字によって空間的な位置を，上付き添字によって時刻を表すことにします．）

フォッカー・プランク方程式の右辺の確率変数に関する微分（ここではこれを空間微分と呼ぶことにします）は中心差分という差分

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\begin{align*}
\pd{}{x} A(x,t)f(x,t) &\to \frac{A_{i+1} f_{i+1} - A_{i-1} f_{i+1} }{ 2 \Delta x}\\
\ppd{}{x} B(x,t)f(x,t) &\to \frac{B_{i+1} f_{i+1} + B_{i-1} f_{i-1} - 2 B_i f_i }{\Delta x^2}
\end{align*}
$$

に置き換えます．これらは，下図のように時空間を離散的な格子点に分割していることを意味します．

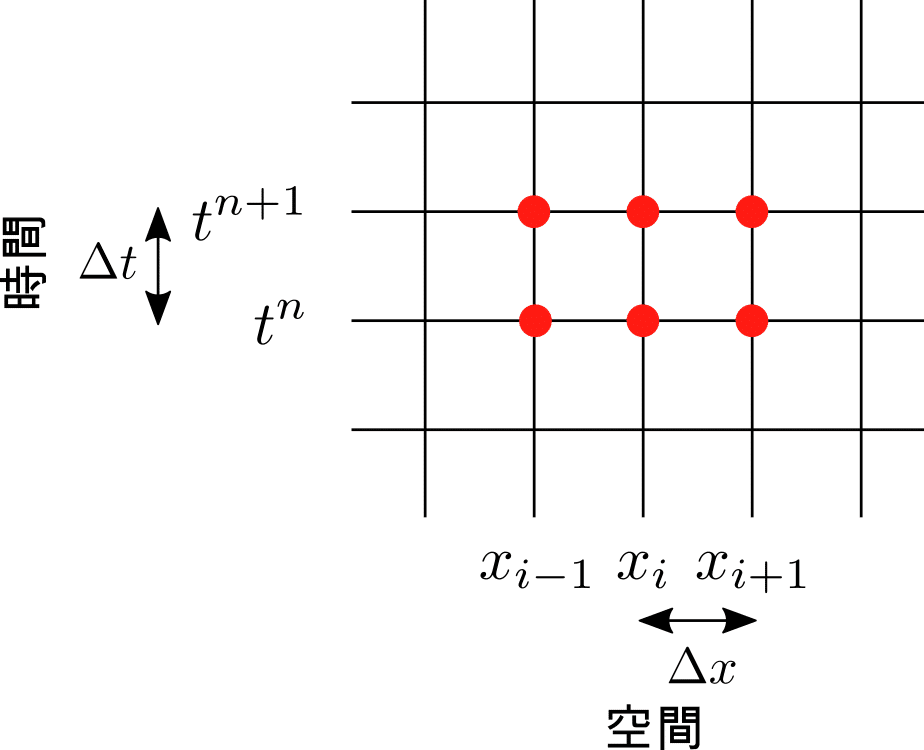
陽解法

今のところ，空間微分について離散化した式にはあえて時刻を表記しませんでした．既に知っている「いま」の状態から未来を考えるので，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\begin{align*}
\pd{}{x} A(x,t)f(x,t) &\to \frac{A_{i+1}^n f_{i+1}^n - A_{i-1}^n f_{i-1}^n }{ 2 \Delta x}\\
\ppd{}{x} B(x,t)f(x,t) &\to \frac{B_{i+1}^n f_{i+1}^n + B_{i-1}^n f_{i-1}^n - 2 B_i^n f_i^n }{\Delta x^2}
\end{align*}
$$

と現在時刻を用いるのが素直です．そうすればフォッカー・プランク方程式は

$$
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
f_i^{n+1} = (1- 2 c_2 B_i^n) f_i^n + \lr{-c_1 A_{i+1}^n + c_2 B_{i+1}^n } f_{i+1}^n +\lr{c_1 A_{i-1}^n + c_2 B_{i-1}^n } f_{i-1}^n
\end{align*}
$$

という形になります．ただし，

$$
\begin{align*}
c_1 = \frac{\Delta t}{2\Delta x}\\
c_2 = \frac{\Delta t}{2 \Delta x^2}
\end{align*}
$$

とおきました．この差分化された方程式によって初期条件から次々と解を求めていくことができます．これは陽解法と言われる基本的な数値計算の解法となります．

安定性の条件

陽解法では，空間の刻み幅を小さくしたら，時間の刻み幅はもっと小さくしなければならないという制限が付きます．物理的に考えてみると，確率密度の拡散的な時間発展とは「確率を保存しながら，確率密度をある重みで平均化していく過程」だと捉えることができ，上式は確かに隣り合う３点の平均を求める式の形をしています．これが確かに平均の意味を持つためには，各係数が正でなければならないことになります．特にドリフト係数が０の場合を考えれば，第一項目について

$$
1 - 2 c_2 B_i^n >0
$$

つまり

$$
\Delta t < \frac{\Delta x^2}{B_i^n}
$$

という制限を満たしている必要があります．私たちが設定した計算の時間間隔は，隣の点からの影響が実際に現象として及ぶ時間よりも短くなくてはならないということを意味しています．そうでないと，本来考慮すべき遠くの点からくる影響を考慮していないことになり，解が不安定になってめちゃくちゃなことになります．（数学的に厳密に示すには，誤差をフーリエ分解して全ての成分が減衰する条件を考えます．）この条件をCFL（Courant-Friedrichs-Lewy）条件ということがあります．この制約があるために，陽解法は好まれないことが多いのです．

陰解法

空間微分について，未来側の時刻をとった

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\begin{align*}
\pd{}{x} A(x,t)f(x,t) &\to \frac{A_{i+1}^{n+1} f_{i+1}^{n+1} - A_{i-1}^{n+1} f_{i-1}^{n+1} }{ 2 \Delta x}\\
\ppd{}{x} B(x,t)f(x,t) &\to \frac{B_{i+1}^{n+1} f_{i+1}^{n+1} + B_{i-1}^{n+1} f_{i-1}^{n+1} - 2 B_i^{n+1} f_i^{n+1} }{\Delta x^2}
\end{align*}
$$

を用いてみます．すると今度は

$$
\newcommand{\lr}[1]{\left(#1\right)}
\newcommand{\slr}[1]{\left[ #1 \right]}
\begin{align*}
f_i^{n+1} = \frac{1}{1+ 2 c_2 B_i^n} \slr{f_i^n + \lr{-c_1 A_{i+1}^{n+1} +c_2 B_{i+1}^{n+1} } f_{i+1}^{n+1} + \lr{c_1 A_{i-1}^{n+1} +c_2 B_{i-1}^{n+1} } f_{i-1}^{n+1} }
\end{align*}
$$

という公式を得ます．この式の右辺には未知の量が含まれているため，全空間について連立して解くことになります．この方法を陰解法といいます．陰解法は連立方程式を解かなければならないため，計算に時間がかかるというデメリットがありますが，こちらには先程のような時間の刻み幅に関する制限はつきません．空間全体の情報を用いて，次の時刻の値を決めているからです．

クランク・ニコルソン法

今まで見てきた方法は，時間については前進差分を用いていて，空間については中心差分を用いていたため，時間については一次精度，空間については二次精度です．時間についての精度を上げるために，時間も中心差分にしようと工夫することを考えます．そのためには，未来の時刻と現在時刻の平均を取ればよさそうです．陽解法で用いた空間差分と陰解法で用いた空間差分の両方を同じ重みで用いることで，

$$
\newcommand{\lr}[1]{\left(#1\right)}
\newcommand{\slr}[1]{\left[ #1 \right]}
\begin{align*}
f_i^{n+1} = \frac{1}{1 + c_2 B_i^{n+1}} \Biggl[
&\lr{1 - c_2 B_i^n } f_i^n + \frac{1}{2} \slr{\lr{-c_1 A_{i+1}^n + c_2 B_{i+1}^n } f_{i+1}^n +\lr{c_1 A_{i-1}^n + c_2 B_{i-1}^n } f_{i-1}^n}\\
&+ \frac{1}{2} \slr{ \lr{-c_1 A_{i+1}^{n+1} +c_2 B_{i+1}^{n+1} } f_{i+1}^{n+1} + \lr{c_1 A_{i-1}^{n+1} +c_2 B_{i-1}^{n+1} } f_{i-1}^{n+1}}
\Biggr]
\end{align*}
$$

とします．この方法をクランク・ニコルソン（Crank-Nicolson）法といいます．この方法も時間刻みに関する条件はつきません．

＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

今回は偏微分方程式の数値解法についてまとめました．次回は，実際にプログラミングする際のアルゴリズムについて解説します．
ところで，コンピュータで計算した結果をただ信用するのでは，妄想を信用するのと大して変わりません．数値計算をしてそれがどれくらい正しいのかを見極めることは重要です．数値計算は実験科学だと認識して，計算方法を変えてチェックしてみることが大切だと思います．

更新履歴
2022/06/16 CFL条件についてちょっと加筆