【量子力学６】物理量と量子操作②【角運動量】

孤立した系では，すべての方向が等しく見えるため，エネルギーの記述が特定の方向に依存しない性質を持つことがよくあります．言い換えると，空間が等方的であることを反映して，ハミルトニアンが回転に対して不変になることが多い．素粒子や原子核などはその例です．このとき，観測の観点から言うと回転運動に対応した固有状態として角運動量状態が出てきます．操作の観点からは，並進運動の生成子が運動量演算子であったのと同じように，回転運動の生成子が角運動量演算子となります．

特に，電磁場をかけることで，ハミルトニアン中に角運動量演算子との相互作用項を導入することができます．人間にとって電磁場は精密に制御ができるため，回転操作によって量子状態を制御し観測する技術は特に発展し，核磁気共鳴や量子コンピュータなど豊かな分野を作っています．核磁気共鳴では，角運動量を持つ原子核が外部磁場に応答する現象を利用して分子構造を解析します．また，量子コンピュータでは，量子ビットの状態を回転操作によって精密に制御しています．この話題はまた別の記事で書くことにしたいと思います．

今回は，量子力学における角運動量の定義やその表現方法について考察します．具体的には，角運動量演算子の代数的性質やその固有状態がどのように記述されるのかを議論します．

円周上の粒子

$${xy}$$平面上にある半径が$${r}$$で一定のリングの上に質量$${m}$$の粒子が束縛されているときを考えます．このときのハミルトニアンは古典力学と同じ形とすれば

$$
\newcommand{\cH}{\mathcal{H}}
\cH = \frac{H}{\hbar} = \frac{L_z^2}{2I\hbar}
$$

と書かれます．ここで，

$$
L_z = r \times p = x p_y - y p_x
$$

は$${z}$$軸周りの角運動量，

$$
I = mr^2
$$

は慣性モーメントです．角運動量や慣性モーメントをこのように定義すれば，ハミルトニアンは自由粒子のハミルトニアンと全く同じ形をしています．したがって，角運動量演算子$${L_z}$$は角度$${\phi}$$をパラメータとして表示すると

$$
\bra{\phi''} L_z \ket{\phi'} = \frac{\hbar}{i} \frac{d}{d\phi'} \delta(\phi'' - \phi')
$$

となり，これは回転運動の生成子である，ということが前回と全く同様の議論の結果として言えます．

ところが，回転運動は自由粒子の並進運動とは決定的に異なる点があります．それは，回転には「ある周期で元に戻る」性質があるという点です．

今回は座標$${\phi}$$について$${2\pi}$$ごとに状態は元に戻ります．したがって，角運動量状態$${\ket{l_z}}$$をある座標に射影した成分

$$
\braket{\phi | l_z} = N e^{i \frac{l_z}{\hbar} \phi}
$$

と座標を$${2\pi}$$ずらした

$$
\braket{\phi + 2\pi|l_z} = N e^{i \frac{l_z}{\hbar} (\phi + 2\pi)}
$$

が等しいとすると，

$$
\frac{l_z}{\hbar} = m \text{（整数）}
$$

でなければなりません．すなわち，角運動量$${L_z}$$の固有値$${l_z}$$は$${\hbar}$$の整数倍の値しか取りません．このとき固有値を規定するパラメータ$${m}$$を角運動量量子数といいます．

ところで，「量子」という言葉は物理量がとびとびの値しか取らないことを意味しています．元々はこの物理量の量子化が謎であり最大の特徴と思われていたわけですが，これは周期性などの境界条件がある場合に定在波が存在できる条件として自然に理解できるようになりました．こうしてみると状態が波動性を持っていることが特に重要かのように思われますが，そもそも量子力学の理論の中で波動性の本質は重ね合わせの原理にあります．「量子力学」という名前はもはや本質を捉えた名前ではありませんが，一度付いた名前はそう変わることはないでしょう．

角運動量の定義と交換関係

先ほど考えた系では「一周すれば元に戻る」という「普通」の状況でしたが，それが考えうる唯一の周期性ではありません．例えとして，メビウスの輪の表面をなぞっていくことを思い起こしてみると，これは一周しただけでは元いた地点の「裏側」にいることになり，元通りとはいきません．メビウスの輪では「二周して元に戻る」という性質があるわけです．二周して元に戻るという状況は角運動量量子数が整数ではなく半整数のときに起こります．こういう二周して元に戻るような回転操作を生成子とするような角運動量もスピンといい量子力学では基本的な役割を果たします．ただし，スピンなら必ず半整数というわけではなく，例えば窒素の原子核のスピンは1を取ります．一般に，我々の住んでいる空間の回転とは直接的には結びついていない，粒子に固有の対称性に由来する角運動量をスピンといいます．そしてスピンは磁場と相互作用する性質を持ちます．スピンと磁場の相互作用の起源はディラック方程式からは自然に出てきますが，非相対論的極限ではそういう性質を持っているものだと深入りせずに思っておきます．質量が重力と相互作用するのも，難しく考えずにそういうものだとしているように．

「一周では元に戻らないといっても，状態ベクトルの符号が変わるだけで，観測にはかからないからそれで良いのだ」と思われていたこともあったようですが，そうではありません．スピン$${1/2}$$を持つ，中性子を使った次のような実験を考えます．中性子ビームを散乱させて二つの経路に分けてからもう一度合流させ干渉させる．このとき片方の経路には磁場をかけてスピン角運動量の位相を回転させる．磁場の強さを変えながら干渉強度を見ると，確かに720度の位相回転周期で干渉強度が変化することがわかりました．状態ベクトルの符号はきちんと検出できる量なのです．

さて，一般の角運動量を理解するために「角運動量は回転操作の生成子である」と本質を捉え直すことにします．$${x}$$軸，$${y}$$軸，$${z}$$軸周りのそれぞれの角運動量演算子を$${J_x,J_y,J_z}$$としたときに，それぞれの軸周りに系を角度$${\phi}$$だけ回転する操作を表すユニタリ変換$${R_x(\phi),R_y(\phi),R_z(\phi)}$$が

$$
\newcommand{\explr}[1]{\exp\!\left(#1\right)}
\begin{align*}
R_x(\phi) &= \explr{-iJ_x \phi}\\
R_y(\phi) &= \explr{-iJ_y \phi}\\
R_z(\phi) &= \explr{-iJ_z \phi}
\end{align*}
$$

のように表現されるはずです．ただし，プランク定数を$${\hbar = 1}$$となるような単位系を用いて角運動量を無次元化しています．

回転操作が持っている性質を調べるときに，その局所的な構造について注目すると扱いやすくなります．これは，回転操作自体は連続パラメータを持つため無限通りの仕方がありますが，局所構造に着目すれば３つの角運動量の交換関係だけが出てきて，それによって回転の数学的構造が定まってしまうという事情からです．

左：x軸周りに回転したあとy軸回りに回転した結果．
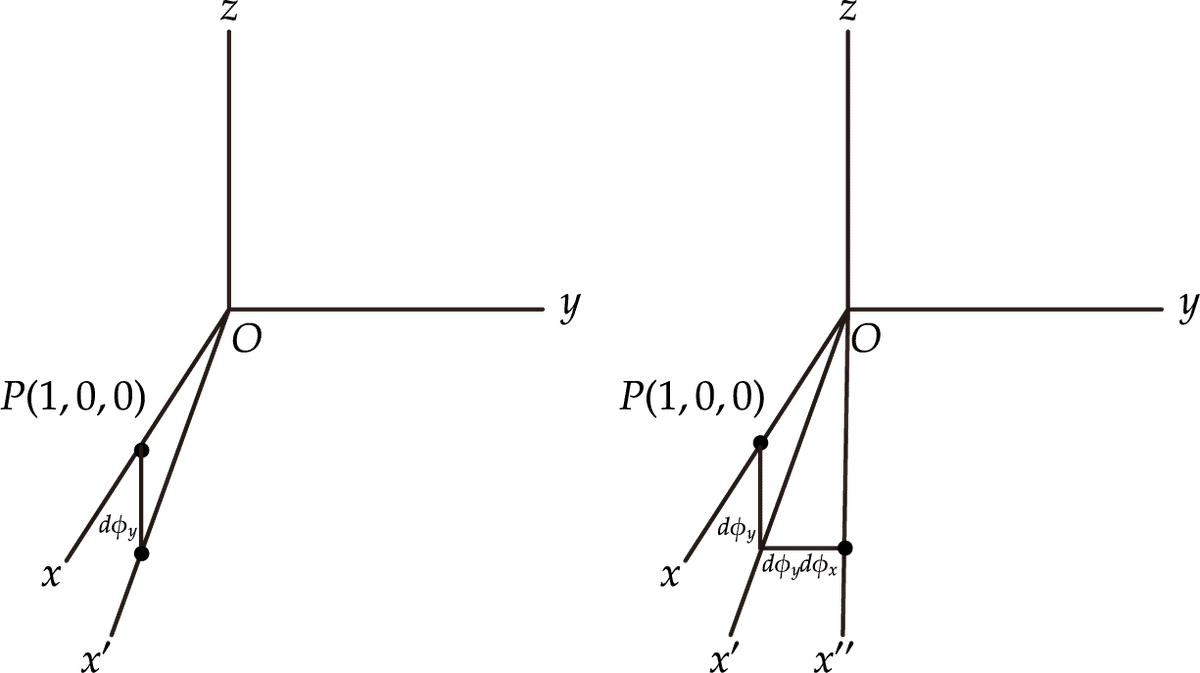
右：y軸周りに回転したあとx軸回りに回転した結果．
シンプルに書くために軌跡を円弧でなく直線で書いている．

回転操作を二回続けて適用したときの効果が，回転の順番によってどのように異なってくるかを調べてみましょう．例えば$${x}$$軸周りに微小回転をしたあと，$${y}$$軸周りに微小回転するときのことを考えてみます．$${x}$$軸上にある点$${P(1,0,0)}$$がどのように動くかを調べてみると，一回めの回転では位置は変わらず，二回めの回転で$${y}$$軸周りに$${d\phi_y}$$移動するため図の左側のようになります．回転の順番を入れ替えて，$${y}$$軸周りに微小回転をしたあと，$${x}$$軸周りに微小回転すると，一回めの回転で位置が$${y}$$軸周りに$${d\phi_y}$$移動したあと，二回めの回転でさらに$${x}$$軸周りに$${d\phi_y d\phi_x}$$移動して，図の右側のようになります．この回転の順番の違いからくる差は，図からわかるように$${z}$$軸周りに$${d\phi_y d\phi_x}$$だけ回転したことによる差と同じです（ほかの軸上の点についても動きを考えてみるとよい）．このことを式で表せば，

$$
\newcommand{\explr}[1]{\exp\!\left(#1\right)}
\explr{-iJ_y d\phi_y}\explr{-iJ_x d\phi_x} - \explr{-iJ_x d\phi_x}\explr{-iJ_y d\phi_y} \\= \explr{-iJ_z d\phi_y d\phi_x} - 1
$$

となります．無限小の量について指数関数を二次まで展開して

$$
\begin{align*}
&(1 - i J_y d\phi_y - \frac{1}{2} J_y^2 d\phi_y^2) (1 - i J_x d\phi_x - \frac{1}{2} J_x^2 d\phi_x^2) \\
&- (1 - i J_x d\phi_x - \frac{1}{2} J_x^2 d\phi_x^2) (1 - i J_y d\phi_y - \frac{1}{2} J_y^2 d\phi_y^2)\\
& = - i J_z d\phi_y d\phi_x
\end{align*}
$$

となりますが，一次の項は消えて二次の項が残り

$$
J_x J_y - J_y J_x = i J_z
$$

という交換関係が出てきます．その他の軸周りの回転も同様に考えれば，

$$
\begin{align*}
[J_x, J_y] &= i J_z,\\
[J_y, J_z] &= i J_x,\\
[J_z, J_x] &= i J_y
\end{align*}
$$

のように交換関係が出てきます．逆に，この交換関係から，回転操作の構造は全てわかります．

実際，本稿の最初に定義した角運動量の組

$$
\begin{align*}
l_x &= y p_z - z p_y\\
l_y &= z p_x - x p_z\\
l_z &= x p_y - y p_x
\end{align*}
$$

は，上の交換関係を満たす例になっていることが，$${\bm{x}}$$と$${\bm{p}}$$の交換関係$${[\bm{x}, \bm{p}]=i}$$から簡単にわかります．

角運動量演算子の固有状態と表現

ここまで，角運動量の$${x,y,z}$$の各成分の演算子を考えてきましたが，空間の等方性から，角運動量の大きさを指定することの方に基本的な物理量としての意味があるはずです．角運動量の大きさを考えるため，角運動量の二乗の演算子

$$
J^2 = J_x J_x + J_y J_y + J_z J_z
$$

を定義します．この演算子は角運動量のどの成分とも交換して，

$$
[J^2, J_i] = 0\ (i = x,y,z)
$$

が成り立つことが$${J_i}$$の交換関係を用いて簡単な計算からわかります．例えば，

$$
[J^2, J_z] = J_x [J_x, J_z] + [J_x, J_z] J_x + J_y [J_y, J_z] + [J_y, J_z] J_y\\ = i ( -J_x J_y - J_y J_x + J_y J_x + J_x J_y ) = 0
$$

であり，他の成分もサイクリックに置き換えていけば同様です．したがって，角運動量の大きさと同時に対角化される観測量として，一つの成分を選ぶことができます．ここでは$${J_z}$$を選びます．等方的なときは$${J_z}$$の固有状態に関しては縮退していますが，磁場をかけると縮退が解けます．

$${J^2}$$と$${J_z}$$の固有値をそれぞれ$${\eta,m}$$と置くことにします．つまり同時固有状態を$${\ket{\eta,m}}$$として

$$
\begin{align*}
J^2 \ket{\eta,m} &= \eta \ket{\eta, m}\\
J_z \ket{\eta,m} &= m \ket{\eta, m}
\end{align*}
$$

と書けます． 全角運動量とその$${z}$$成分の値を比べたら，全角運動量の方が常に大きいことが予想されます．これは$${J^2}$$と$${J_z^2}$$を比べると，

$$
J^2 - J_z^2 = J_x^2 + J_y^2
$$

が得られ，エルミート演算子の二乗の対角要素は非負であるために

$$
\bra{\eta, m} (J^2 - J_z^2) \ket{\eta, m} = \eta - m^2 \geq 0
$$

がわかります．したがって，角運動量の$${z}$$成分の値は，$${ - \sqrt{\eta} \leq m \leq \sqrt{\eta}}$$の範囲に制限されることになります．

角運動量演算子の固有値をさらに詳しく調べるために，$${J_x,J_y}$$が角運動量の固有状態に作用したときのことも考えます．これらをこのまま使うのではなく，次の演算子

$$
J_\pm = J_x \pm i J_y
$$

を用いると便利です．これらは昇降演算子と呼ばれますが，そう呼ばれる理由は，角運動量の固有状態に作用したときに$${z}$$成分の固有値を一つ増やしたり減らしたりするからです．

実際に昇降演算子の作用を次の計算によって確認しましょう：

$$
\begin{align*}
J_z J_\pm \ket{\eta,m} &= ([J_z, J_\pm] + J_\pm J_z) \ket{\eta,m}\\
&= (m \pm 1) J_\pm \ket{\eta,m}.
\end{align*}
$$

この計算には昇降演算子についての次の簡単な計算でわかる交換関係

$$
[J_z, J_\pm] = \pm J_\pm
$$

を用いました．この結果を見るとわかることは，昇降演算子を固有状態にかけた状態も$${J_z}$$の固有状態のままでありますが，固有値が$${1}$$増減しているということです．つまり，

$$
J_\pm \ket{\eta,m} \propto \ket{\eta, m\pm 1}
$$

と表せます．比例定数はあとで求めましょう．

ところが，$${J_z}$$の固有値には全角運動量の大きさで決まる範囲の制限があったので，無限に昇降演算子を掛け続けて固有値を増やし（減らし）続けることはできません．したがって，

$$
\begin{align*}
J_+ \ket{\eta, m_\mathrm{max}} = 0\\
J_- \ket{\eta, m_\mathrm{min}} = 0
\end{align*}
$$

を満たすような$${m_\mathrm{max},m_\mathrm{min}}$$が存在することによって，これを超えて固有値が増減することを防がなければなりません．この第一式に$${J_-}$$を，第二式に$${J_+}$$を作用させると，

$$
J_\mp J_\pm = J^2 - J_z(J_z\pm 1)
$$

から

$$
\eta - m_\mathrm{max} (m_\mathrm{max} + 1) = 0\\
\eta - m_\mathrm{min} (m_\mathrm{min} - 1) = 0
$$

が得られます．この二つの式から$${\eta}$$を消去すると，$${m_\mathrm{max} > m_\mathrm{min}}$$であることも考慮すると

$$
m_\mathrm{max} = - m_\mathrm{min}
$$

を満たさなければならいことがわかります．また，$${\ket{\eta,m_\mathrm{min}}}$$に上昇演算子$${J_+}$$を何回もかけると$${\ket{\eta,m_\mathrm{max}}}$$に達すると考えられるため，

$$
m_\mathrm{max} = m_\mathrm{min} + (\text{整数})
$$

です．したがって，$${m_\mathrm{max}}$$として可能な値は

$$
m_\mathrm{max} = 0, \frac{1}{2}, 1, \frac{3}{2}, 2, \ldots
$$

とわかります．以降，慣習的に$${m_\mathrm{max} = j}$$と置き直しておきます．与えられた$${j}$$に対して，許される$${m}$$の値は，

$$
-j \leq m \leq j
$$

の範囲の$${1}$$ずつ異なる値です．また

$$
\eta = j(j+1)
$$

となっています．

まとめると，

$$
\begin{align*}
J^2 \ket{j,m} &= j(j+1) \ket{j,m}, \ (j\text{は整数または半整数})\\
J_z \ket{j,m} &= m \ket{j,m} ,\ (m = -j, -j+1, \ldots, j-1, j)
\end{align*}
$$

となります．

$${J^2}$$の固有値が$${j^2}$$にならずに$${j(j+1)}$$となって余分な項がついたのはなぜでしょうか．元を正せば，角運動量演算子の$${x,y}$$成分が交換しないことから来ています．つまり，角運動量ベクトルの方向が不確定であることから生じていて，どんなに角運動量を奪ったとしても$${0}$$にはならないということになります．

角運動量演算子の固有値がわかったので，その行列表現を求めることは簡単です．まずは，

$$
\begin{align*}
\bra{j',m'} J^2 \ket{j,m} &= j(j+1)\ \delta_{j',j} \delta_{m',m},\\
\bra{j',m'} J_z \ket{j,m} &= m \ \delta_{j',j} \delta_{m',m}
\end{align*}
$$

が得られます．$${J_\pm}$$の行列表現を求めるためには，

$$
\begin{align*}
\bra{j,m} J_\pm^{\dagger} J_\pm \ket{j,m} &= \bra{j,m} (J^2 - J_z(J_z\pm 1))\\
&= j(j+1) - m(m \pm 1)\\
&= (j \mp m) (j \pm m + 1)
\end{align*}
$$

を考えればよい．$${J_\pm \ket{j,m}}$$は$${\ket{j,m\pm 1}}$$に比例するのでした．したがって，上式の左辺はその比例定数の二乗に等しく，それゆえ

$$
J_\pm \ket{j,m} = \sqrt{(j \mp m) (j \pm m + 1)} \ket{j,m+1}
$$

が得られます．これから，行列表現は

$$
\bra{j',m'} J_\pm \ket{j,m} = \sqrt{(j \mp m) (j \pm m + 1)}\ \delta_{j',j} \delta_{m',m}
$$

と決まります．

例えば，$${j= 1/2}$$および$${j=1}$$と与えられたときの演算子の行列表現を書いてみます．$${m}$$が最大値$${j}$$をとるときの要素を1行1列めに書くことにします．
$${j = 1/2}$$のとき：

$$
\begin{align*}
J^2 &= \frac{3}{4}\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}\\
J_z &= \frac{1}{2}\begin{pmatrix}
1 & 0\\
0 & -1
\end{pmatrix}\\
J_+ &= \begin{pmatrix}
0 & 1\\
0 & 0
\end{pmatrix}\\
J_- &= \begin{pmatrix}
0 & 0\\
1 & 0
\end{pmatrix}\\
J_x &= \frac{1}{2}\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}\\
J_y &= \frac{1}{2}\begin{pmatrix}
0 & -i\\
i & 0
\end{pmatrix}
\end{align*}
$$

$${j = 1}$$のとき：

$$
\begin{align*}
J^2 &= 2\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{pmatrix}\\
J_z &= \frac{1}{2}\begin{pmatrix}
1 & 0 & 0\\
0 & 0 & 0\\
0 & 0 & -1
\end{pmatrix}\\
J_+ &= \sqrt{2} \begin{pmatrix}
0 & 1 & 0\\
0 & 0 & 1\\
0 & 0 & 0
\end{pmatrix}\\
J_- &= \sqrt{2} \begin{pmatrix}
0 & 0 & 0\\
1 & 0 & 0\\
0 & 1 & 0
\end{pmatrix}\\
J_x &= \frac{1}{\sqrt{2}}\begin{pmatrix}
0 & 1 & 0\\
1 & 0 & 1\\
0 & 1 & 0
\end{pmatrix}\\
J_y &= \frac{1}{\sqrt{2}}\begin{pmatrix}
0 & -i & 0\\
i & 0 & -i\\
0 & i & 0
\end{pmatrix}
\end{align*}
$$

となります．ここで，$${J_x,J_y}$$は昇降演算子と関係づいているのでそこから求めました．また，$${j=1/2}$$のときの$${J_x,J_y,J_z}$$に現れた次の行列

$$
\begin{align*}
Z &= \begin{pmatrix}
1 & 0\\
0 & -1
\end{pmatrix}\\
X &= \begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}\\
Y &= \begin{pmatrix}
0 & -i\\
i & 0
\end{pmatrix}
\end{align*}
$$

はパウリ行列と呼ばれます．

軌道角運動量と位置表示

スピンではなく，実際の空間上での回転運動と直接結びついた角運動量（軌道角運動量）については，位置での表現も考えておきます．軌道角運動量に対しては慣例として演算子の記号を$${J}$$の代わりに$${L}$$とします．

球面座標系

座標は球面座標によって，$${(\theta,\phi)}$$で与えます．角度の定義は図のようにします．回転は原点からの距離を変えることはないため，距離はなんでもよい．$${L_z}$$に対しては，すでに

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\bra{\theta,\phi} L_z \ket{\psi} = -i \pd{}{\phi} \braket{\theta,\phi|\psi}
$$

となることを知っています．（ただし$${\hbar = 1}$$としています．）軌道角運動量の$${x}$$成分と$${y}$$成分は

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
\bra{\theta,\phi} L_x \ket{\psi} &= -i \lr{ -\sin\phi \pd{}{\theta} - \cot \theta \cos \phi \pd{}{\phi} }\braket{\theta,\phi|\psi}\\
\bra{\theta,\phi} L_y \ket{\psi} &= -i \lr{ \cos\phi \pd{}{\theta} - \cot\theta \sin\phi \pd{}{\phi} } \braket{\theta,\phi|\psi}
\end{align*}
$$

となることを示すことができます．それを示すには，直交座標系で角運動量演算子を書いておいてから球面座標系表示に直すというやり方をするのが一般的ですが，以下では球面座標系で直接示しましょう．

図のように，$${x}$$軸から測った角度を$${\alpha}$$，$${x}$$軸周りの角度を$${\beta}$$とおいた別の球面座標系を考えます．このように置くと元の球面座標系における$${z}$$軸とこの球面座標系における$${x}$$軸が対等になるので，$${L_x}$$は

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\bra{\alpha,\beta} L_x \ket{\psi} = -i \pd{}{\beta} \braket{\alpha,\beta|\psi}
$$

と書かれるはずです．異なる座標系間で微分演算子は

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{}{\beta} = \pd{\theta}{\beta} \pd{}{\theta} + \pd{\phi}{\beta} \pd{}{\phi}
$$

と変換されるため，これを計算すれば元の球面座標系での微分演算子の表式がわかります．

図を頼りにすると

$$
\begin{align*}
\sin\phi \tan\beta &= \cot \theta\\
\cos\alpha &= \sin\theta \cos\phi
\end{align*}
$$

という関係があることがわかります．これらを両辺$${\beta}$$について微分して整理すると

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
\cos\phi\sin\theta\cos\theta \pd{\phi}{\beta} + \sin\phi \pd{\theta}{\beta} &= \cos^2 \theta + \sin^2 \theta \sin^2 \phi\\
\cos\theta\cos\phi \pd{\theta}{\beta} - \sin\theta\sin\phi \pd{\phi}{\beta} &= 0
\end{align*}
$$

が得られます．これらを連立して解くことで，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
\pd{\theta}{\beta} &= - \sin\phi\\
\pd{\phi}{\beta} &= - \cot\theta\cos\phi
\end{align*}
$$

が得られ，したがって

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
\pd{}{\beta} = - \sin\phi \pd{}{\theta} - \cot\theta\cos\phi \pd{}{\phi}
\end{align*}
$$

がわかりました．$${y}$$軸に関しても同様のことを行えば，示したかった軌道角運動量の球面座標表示が得られます．

昇降演算子については

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
\bra{\theta,\phi} L_\pm \ket{\psi} = -i e^{\pm i \phi} \lr{\pm i \pd{}{\theta} - \cot\theta \pd{}{\phi}} \braket{\theta,\phi | \psi}
\end{align*}
$$

であり，$${L^2 = L_z^2 + (L_+ L_- + L_- L_+)/2}$$は

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
\bra{\theta,\phi} L^2 \ket{\psi} = - \lr{
\frac{1}{\sin^2\theta} \ppd{}{\phi} + \frac{1}{\sin\theta} \pd{}{\theta}\lr{\sin\theta \pd{}{\theta}}
}\braket{\theta,\phi |\psi}
\end{align*}
$$

のように書くことができます．球面座標系でのラプラシアンが

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
\nabla^2 = \frac{1}{r^2}\lr{ \pd{}{r} \lr{r^2 \pd{}{r}}
\frac{1}{\sin^2\theta} \ppd{}{\phi} + \frac{1}{\sin\theta} \pd{}{\theta}\lr{\sin\theta \pd{}{\theta}}
}
\end{align*}
$$

と書かれるので，全角運動量演算子とラプラシアンの角度部分は$${1/r^2}$$の因子を除いて一致していることがわかります．

次に，固有状態についての位置表示を求めましょう．固有値方程式は

$$
\begin{align*}
L^2 \ket{l,m} &= l(l+1) \ket{l,m}\\
L_z \ket{l,m} &= m \ket{l,m}
\end{align*}
$$

であったから，この左辺に求めた角運動量演算子の位置表示を用いて

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\ppd}[2]{\frac{\partial^2 #1}{\partial #2^2}}
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
\lr{
\frac{1}{\sin^2\theta} \ppd{}{\phi} + \frac{1}{\sin\theta} \pd{}{\theta}\lr{\sin\theta \pd{}{\theta}}
}\braket{\theta,\phi | l,m} &= l (l+1) \braket{\theta,\phi | l,m}\\
-i \pd{}{\phi} \braket{\theta,\phi |l,m} &= m \braket{\theta,\phi |l,m}
\end{align*}
$$

が得られます．これらの微分方程式を満たす関数を球面調和関数といい，$${\braket{\theta,\phi | l,m} = Y_l^m (\theta,\phi)}$$と書きます．

球面調和関数を求めるために，角運動量の$${z}$$成分が最大の場合である$${Y_l^l}$$について考え，そこに下降演算子を掛けることで一般の球面調和関数を求めるという方法を取りましょう．

$$
L_+ \ket{l,l} = 0
$$

すなわち，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\lr}[1]{\left(#1\right)}
-i e^{ i \phi} \lr{ i \pd{}{\theta} - \cot\theta \pd{}{\phi}} Y_l^l(\theta,\phi) =0
$$

を考えます．
$${L_z}$$に関する固有値方程式から，$${Y_l^m}$$の$${\phi}$$に関する依存性が

$$
Y_l^m \propto e^{im\phi}
$$

となっていることがわかって，このことを用いると，

$$
Y_l^l = c(l) e^{il\phi} \sin^l \theta
$$

が得られます．球面調和関数の内積が立体角$${d\Omega = \sin\theta d\phi d\theta}$$での積分であることから，規格化の条件は

$$
\int_0^{2\pi} d\phi \int_{-1}^{1} d\theta\ \sin\theta \ Y_l^l(\theta,\phi) Y_l^l(\theta,\phi) = 1
$$

であり，ここから規格化定数$${c(l)}$$は

$$
c(l) = \frac{(-1)^l}{2^l l!} \sqrt{\frac{(2l+1)(2l)!}{4\pi}}
$$

と決まります．

下降演算子を作用させると

$$
L_- \ket{l,m} = \sqrt{(l+m)(l-m+1)} \ket{l,m-1}
$$

すなわち

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\lr}[1]{\left(#1\right)}
-i e^{-i\phi} \lr{- i \pd{}{\theta} - \cot \theta \pd{}{\phi}} Y_l^m = \sqrt{(l+m)(l-m+1)} Y_l^{m-1}
$$

となることを用いると，球面調和関数が全て得られます：

$$
Y_l^m (\theta,\phi) = \frac{(-1)^l}{2^l l!} \sqrt{\frac{(2l+1)(l+m)!}{4\pi}(l-m)!}\ e^{im\phi} \frac{1}{\sin^m \theta} \frac{d^{l-m}}{d(\cos\theta)^{l-m}} (\sin\theta)^{2l}.
$$

スピン1/2の系

ここでは例としてスピン$${1/2}$$の系を考え，回転操作の効果を確認します．スピン角運動量演算子は

$$
\begin{align*}
S_z &= \frac{1}{2}\begin{pmatrix}
1 & 0\\
0 & -1
\end{pmatrix}\\
S_x &= \frac{1}{2}\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}\\
S_y &= \frac{1}{2}\begin{pmatrix}
0 & -i\\
i & 0
\end{pmatrix}
\end{align*}
$$

と書けます．慣例としてスピンに対しては演算子の記号を$${J}$$ではなく$${S}$$とします．

$${z}$$軸周りの角度$${\phi}$$の回転を表す演算子は

$$
R(\phi) = e^{-i S_z \phi}
$$

と書けます．行列表記に直すには，指数を展開してから，パウリ行列の性質

$$
X^2 = Y^2 = Z^2 = I
$$

を用いればよく

$$
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
R(\phi) &= e^{-i S_z \phi}\\
&= 1 - i S_z \phi - \frac{1}{2} S_z^2 \phi^2 + \frac{i}{3!} S_z^3 \phi^3 + \cdots\\
&= 1 - i Z \frac{\phi}{2} - \frac{1}{2} I \lr{\frac{\phi}{2}}^2 + \frac{i}{3!} Z \lr{\frac{\phi}{2}}^3 + \cdots\\
&= I \cos \lr{\frac{\phi}{2}} - i Z \sin \lr{\frac{\phi}{2}}\\
&= \begin{pmatrix}
e^{-i\frac{\phi}{2}} & 0 \\
0 & e^{i\frac{\phi}{2}}
\end{pmatrix}
\end{align*}
$$

となります．
ここに半角$${\phi/2}$$が現れていることから，任意の状態ベクトルに回転が作用したときに，$${4\pi}$$回転して初めて元に戻ることがわかります．$${2\pi}$$回転だと

$$
\begin{align*}
R(2\pi) = \begin{pmatrix}
-1 & 0\\
0 & -1
\end{pmatrix}
\end{align*}
$$

となって，状態の符号が変わるという結果が得られることがわかります．

スピン角運動量の各成分は回転演算子の作用後にどのようになるでしょうか．ベーカー・キャンベル・ハウスドルフの補助定理を用いると$${S_x}$$に対して計算が次のようにできます：

$$
\begin{align*}
e^{i S_z \phi} S_x e^{-i S_z \phi} &= S_x + i\phi [S_z, S_x] - \frac{1}{2} \phi^2 [S_z, [S_z, S_x]]\\
&= S_x (1- \frac{1}{2}\phi^2 + \cdots) - S_y (\phi - \frac{1}{3!} \phi^3 +\cdots)\\
&= S_x \cos\phi - S_y \sin\phi .
\end{align*}
$$

同様にして

$$
e^{i S_z \phi} S_y e^{-i S_z \phi} = S_y \cos\phi - S_x \sin\phi
$$

であり，また$${z}$$成分に関しては演算子が交換するために

$$
e^{i S_z \phi} S_z e^{-i S_z \phi} = S_z
$$

と変わらない．したがって，ベクトル演算子に対しては半角は現れず，通常のベクトルのように$${2\pi}$$回転で元に戻ることがわかります．

スピンを持つ粒子に磁場をかけるとき，ハミルトニアンは

$$
\mathcal{H} = -\gamma \bm{S}\cdot \bm{B}
$$

と書けます．$${\gamma}$$は磁気回転比と呼ばれる定数です．磁場を$${z}$$軸方向に均一な磁場とすると，

$$
\mathcal{H} = -\gamma B_z S_z = \omega_0 S_z
$$

とシンプルになります．$${-\gamma B_z = \omega_0}$$と置きました．これはラーモア周波数と呼ばれます．このような物理的な状況が，スピンの$${z}$$軸周りの角度$${\phi = \omega t}$$の回転運動（歳差運動）を引き起こすことが明らかです．

今回のまとめ

角運動量は回転操作の生成子である．回転操作には周期性があるため，角運動量量子数は不連続な値を取り，それは整数または半整数である．角運動量量子数が半整数のものは2周回転してはじめて状態がもとに戻る周期性を持ち，通常の空間とは異なりスピン角運動量はこのような対称性を持つことがある．角運動量量子数が整数のものに対しては位置での表示を考えることができ，その角運動量演算子の固有状態は球面調和関数になる．これらの結果は角運動量演算子の各成分の交換関係から導くことができる．