【物理数学】マルコフ過程とマスター方程式【確率論②】

マルコフ（Markov）過程とは，過去の記憶とは独立に次の運動が起こるような確率過程です．物理現象は歴史によらないということ，たとえばボールの運動はそのボールがどの工場でどう生産されたかにはよらず，今の状況さえ考えればよいということは，ある種物理学の信念とも言えるでしょう．そのため，マルコフ過程は物理学の基本過程と言ってもよいほどで，物理的な過程を理想化するときにしばしば重要な役割を果たします．

マルコフ過程は条件付き確率を用いて定義されます．前回定義したように，過去のいろいろな時点での条件がわかっているとき，次の時点においてある状況になる確率は条件付き確率

$$
P(x,t \mid x',t'; x'', t'',\ldots)
$$

で表されます．ここで，時間は

$$
t > t' > t'' > \cdots
$$

の順に書いています．（この表記法では右から左に式を眺めるのがコツです．）過去の全ての影響が現在の状態に集約されていると考えてよいとき，上の条件付き確率が二点間のみの遷移を表す条件付き確率，プロパゲータに一致し

$$
P(x,t \mid x',t'; x'', t'',\ldots) = P(x,t \mid x',t')
$$

が成り立つとできます．このような確率過程をマルコフ過程といいます．

マルコフ過程の時間発展方程式

マルコフ過程では，確率密度の時間発展がつぎのような単純な形の微分方程式で表されます：

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{}{t} f(x,t) = \mathcal{A}(x,t) f(x,t)
$$

ただし，$${\mathcal{A}(t)}$$は確率の規格化を保つような線形演算子とします．これは一階の微分方程式になっています．二階微分方程式だと次の状態を予測するために今の状態だけでなく直前の状態まで知る必要があるということですが，一階微分ということは今の状態さえわかれば次の状態もわかるということです．このことから，この式で表される過程がマルコフ過程であることがわかります．次のステップでの状態を知るためには右辺にあるように何らかの演算子$${\mathcal{A}(t)}$$をかけるわけですが，この演算子を確率的演算子と呼ぶことにします．

確率的演算子は，確率の規格化を保つために，両辺を全状態について積分したときに

$$
\int dx \mathcal{A}(x,t) f(x,t) = 0
$$

を満たすことが必要になります．

以下では，確率的演算子の具体的な形も含めて，この微分方程式をマルコフ過程の定義から導きます．それがいわゆるマスター方程式と呼ばれるものになります．

チャップマン-コルモゴロフ方程式

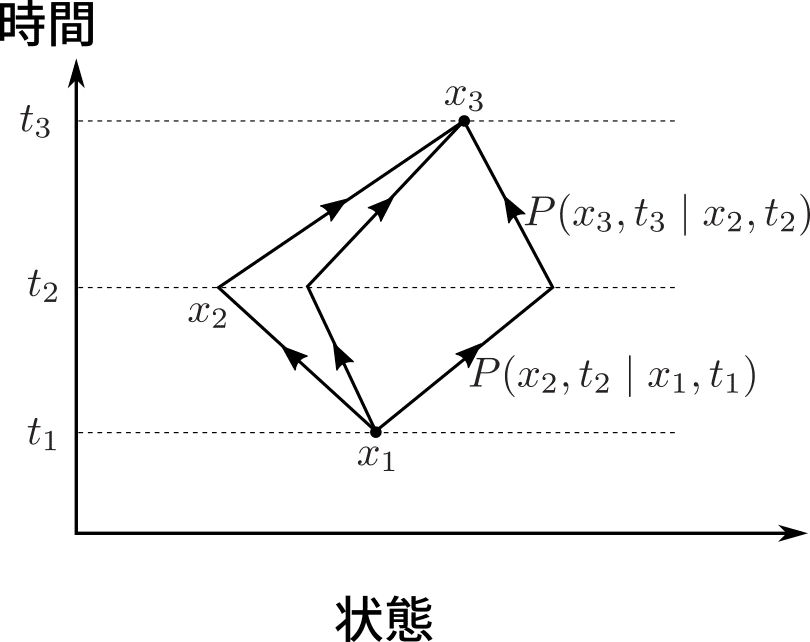
マルコフ過程なら，三点以上をとったときの同時確率密度も，プロパゲータ（と初期状態）のみから構築することができるという単純な性質を持ちます．マルコフ過程のとき，三点の同時確率密度は

$$
\begin{align*}
f(x_3,t_3;x_2,t_2;x_1,t_1) &= P(x_3,t_3\mid x_2,t_2, x_1,t_1) f(x_2,t_2;x_1,t_1)\\
&= P(x_3,t_3 \mid x_2, t_2) P(x_2,t_2 \mid x_1,t_1) f(x_1,t_1)
\end{align*}
$$

と書けます．一行目の式はマルコフ過程に限らず成り立つただの恒等式です．二行目に移る際に，マルコフ過程の定義を用いています．

上式の両辺を中間地点について和をとることにより周辺化すると

$$
f(x_3,t_3;x_1,t_1) = f(x_1,t_1) \int dx_2 P(x_3,t_3 \mid x_2, t_2) P(x_2,t_2 \mid x_1,t_1)
$$

となるので，これを両辺初期分布で割り算すると，マルコフ過程のときにプロパゲータが満たす条件として

$$
P(x_3,t_3 \mid x_1,t_1) = \int dx_2 P(x_3,t_3 \mid x_2, t_2) P(x_2,t_2 \mid x_1,t_1)
$$

が導かれます．これをチャップマン-コルモゴロフ（Chapman-Kolmogorov）方程式と呼びます．チャップマン-コルモゴロフ方程式の意味は下図のように直感的に理解できます．最終地点までの変化を表すには，中間地点を経由させて積をとってから，あらゆる中間地点について足せば良いのです．

マスター方程式

プロパゲータの時間発展を表す微分方程式を導くために，小さな時間幅を用いて

$$
t_3 = t_2 + \Delta t
$$

と考えることによって

$$
P(x_3,t_3 \mid x_2, t_2) = P(x_3,t_2+\Delta t \mid x_2, t_2)
$$

と書き換えます．一般にこのプロパゲータについて，時間幅を小さくする極限で

$$
\lim_{\Delta t \to 0} P(x_3,t_2+\Delta t \mid x_2, t_2) = \delta(x_3 - x_2)
$$

が成り立ちます（右辺はデルタ関数）．なぜなら，時間を待たずにすぐに観測する極限では，全く同じ状態が観測される確率が$${1}$$になるべきだからです．したがって，

$$
P(x_3,t_2+\Delta t \mid x_2, t_2) = \delta (x_3 - x_2) + O(\Delta t)
$$

と展開されるはずです．さらに今回は，ランダウの記号で表した時間幅の一次のオーダーの項は

$$
O(\Delta t) = -\Gamma(x_2,t) \Delta t\ \delta(x_3 - x_2) + W(x_3 \mid x_2, t_2) \Delta t + O(\Delta t^2)
$$

と展開できると仮定しましょう．この短時間でそのままの状態にととどまる確率が減少して（第一項），代わりに別の状態に移る確率が増えること（第二項）を意味しています．この意味でいま導入した記号を

$$
\begin{align*}
\Gamma(x,t) &: \text{減衰速度（decay rate）}\\
W(x \mid x', t) &: \text{遷移速度（transition rate）}
\end{align*}
$$

と呼ぶのが適切でしょう．別の状態に移る遷移速度について全て和をとったものは，減衰速度でもあるはずなので，

$$
\Gamma(x',t) = \int dx\ W(x\mid x', t)
$$

が成り立っているはずです．これは遷移確率（プロパゲータ）の規格化の条件

$$
\int dx_3\ P(x_3, t_3 \mid x_2, t_2) = 1
$$

から確かに成り立つことがすぐに確かめられます．

書き換えたプロパゲータをチャップマン-コルモゴロフ方程式に代入すれば

$$
\newcommand{\lr}[1]{\left(#1\right)}
\begin{align*}
&P(x_3,t_2 + \Delta t \mid x_1,t_1)\\
&= \int dx_2 \lr{(1 - \Gamma(x_2,t_2) \Delta t ) \delta(x_3 - x_2) + W(x_3 \mid x_2, t_2) \Delta t } P(x_2,t_2 \mid x_1,t_1)\\
&= (1- \Gamma(x_3,t_2) \Delta t) P( x_3, t_2 \mid x_1, t_1) + \int dx_2 W(x_3 \mid x_2, t_2) \Delta t P (x_2, t_2 \mid x_1, t_1)
\end{align*}
$$

書き直して

$$
\begin{align*}
&\frac{P(x_3,t_2 + \Delta t \mid x_1,t_1) - P( x_3, t_2 \mid x_1, t_1)}{\Delta t} \\
&=-\Gamma(x_3,t_2) P(x_3,t_2 \mid x_1,t_1) + \int dx_2 W(x_3 \mid x_2, t_2) P (x_2, t_2 \mid x_1, t_1)\\
&= \int dx_2 \Bigl[
-W(x_2\mid x_3,t_2) P(x_3,t_2 \mid x_1,t_1) + W(x_3 \mid x_2, t_2) P (x_2, t_2 \mid x_1, t_1)
\Bigr]
\end{align*}
$$

となります．この時間間隔を無限小にする極限をとれば微分形として

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{}{t} P(x,t\mid x_0,t_0) = \int dx' \Bigl[
-W(x' \mid x,t) P(x,t \mid x_0,t_0) + W(x \mid x', t) P (x', t \mid x_0, t_0)
\Bigr]
$$

が得られます．（ただし変数の見た目を変えました．）これが微分形のチャップマン-コルモゴロフ方程式のやや特別な場合（遷移速度の存在を仮定しているという意味で）であって，マスター方程式と呼ばれます．

任意の初期分布に対してプロパゲータをかけて，初期値に対して積分（周辺化）してやれば，ある時刻において確率変数がある値を取る確率密度に関する式となり

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\pd{}{t} f(x,t) = \int dx' \Bigl[
-W(x' \mid x,t) f(x,t) + W(x \mid x', t) f(x', t)
\Bigr]
$$

となります．こちらもマスター方程式といいます．右辺の積分操作は線形演算子となっていて，さらに確率の規格化も保つことが確かめられます．こうして，目的のマスター方程式を導くことができました．

マスター方程式の意味を理解するために，ここで簡単な具体例を考えてみることにします．（この例題にちなんで（？）ヘッダー画像は実家で飼っているクランウェルツノガエルにしてみました…かわいいですね…）

例題
カエルたちが石1，石2の上を飛び移っています．カエルは今いる石だけから判断して，飛び移るかどうかを確率的に決めるとします．時間が 1 経ったのちに石1から石2に飛び移る確率を0.6，とどまる確率を0.4とし，石2から石1に飛び移る確率を0.2，とどまる確率を0.8とします．このカエルたちはこの2つの石の上以外にはどこへも行かないし，カエルどうしで話し合ったりなどはしないとします（つまり孤立系を考え，カエルどうしは独立ということ．なんだか哀れですが......）．カエルの分布の時間変化を考えよう．

この問題を図示すると下のようになります．この図の見方は説明するまでもないでしょう．（ちなみに何かと何かの関係を繋いだこういう図のことを「グラフ」と言ったりします．）

この問題では遷移速度が時間によらないので，定常的であるといいます．
とりあえず一匹のカエルだけのときを考えて，そのカエルがどちらの石にいるか（という事象にラベル付けした数字）を確率変数と思ってやってみます．この場合，確率変数の実現値は，1か2の値を取ります．遷移速度は

$$
\begin{align*}
W(1\mid 1) = 0.4 \\
W(2\mid 1) = 0.6 \\
W(2\mid 2) = 0.2 \\
W(2\mid 2) = 0.8
\end{align*}
$$

と書かれるので，マスター方程式は

$$
\begin{align*}
\begin{pmatrix}
\dot{p}_1\\
\dot{p}_2
\end{pmatrix}
&=
\begin{pmatrix}
- p_1\\
- p_2
\end{pmatrix}
+
\begin{pmatrix}
0.4 & 0.2 \\
0.6 & 0.8
\end{pmatrix}
\begin{pmatrix}
p_1\\
p_2
\end{pmatrix}\\
&= \begin{pmatrix}
-0.6 & 0.2\\
0.6 & -0.2
\end{pmatrix}
\begin{pmatrix}
p_1\\
p_2
\end{pmatrix}
\end{align*}
$$

となります．ただし，離散的なのでマスター方程式に現れる積分操作は和に置き換えられ，行列によって表現できました．また，確率関数（離散的なので確率密度の代わりにこう呼びます）はベクトルで表現することができて

$$
\begin{align*}
f(1,t) = p_1 \\
f(2,t) = p_2
\end{align*}
$$

と置きました．

この方程式をどんな方法で解いてもいいのですが，今回は行列を用いた方法で解いてみます．右辺に現れた行列を

$$
\mathcal{A} = \begin{pmatrix}
-0.6 & 0.2\\
0.6 & -0.2
\end{pmatrix}
$$

と置きます．この行列の固有方程式

$$
\begin{align*}
\mathcal{A} \ket{\lambda} = \lambda \ket{\lambda}\\
\bra{\lambda} \mathcal{A} = \lambda \bra{\lambda}
\end{align*}
$$

を考えます．量子力学でよく用いられるディラックの記法を真似てベクトルを「ブラケット」で記しました．
固有値を求めると $${0}$$， $${-0.8}$$で，固有値 $${0}$$ に対応する縦横それぞれの固有ベクトルは

$$
\ket{0} =
\begin{pmatrix}
0.25 \\
0.75
\end{pmatrix},\quad
\bra{0} =
\begin{pmatrix}
1 & 1
\end{pmatrix}
$$

固有値 $${-0.8}$$ に対応する縦横それぞれの固有ベクトルは

$$
\ket{-0.8} =
\begin{pmatrix}
1\\
-1
\end{pmatrix},\quad
\bra{-0.8} =
\begin{pmatrix}
0.75 & -0.25
\end{pmatrix}
$$

と求められます．同じ固有値に属する縦横の固有ベクトル同士での内積が

$$
\braket{\cdot\mid\cdot} = 1
$$

になるように規格化してあります．また，異なる固有値に属する固有ベクトルで内積をとると0になる直交性がいつも成り立ちます．規格直交性から，完全性関係と呼ばれる関係式

$$
\sum_\lambda \ket{\lambda}\bra{\lambda} = 1 \text{ （1は単位行列）}
$$

が成り立ちますが，今回の具体例でも確かめられます．すなわち，今回の例では

$$
\begin{align*}
\sum_\lambda \ket{\lambda}\bra{\lambda} &= \ket{0}\bra{0} + \ket{-0.8}\bra{-0.8}\\
&=
\begin{pmatrix}
0.25 \\
0.75
\end{pmatrix}
\begin{pmatrix}
1 & 1
\end{pmatrix}
+
\begin{pmatrix}
1\\
-1
\end{pmatrix}
\begin{pmatrix}
0.75 & -0.25
\end{pmatrix}\\
&= \begin{pmatrix}
0.25 & 0.25\\
0.75 & 0.75
\end{pmatrix}
+
\begin{pmatrix}
0.75 & -0.25\\
-0.75 & 0.25
\end{pmatrix}
= \begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}
\end{align*}
$$

となっていて，完全性関係が成り立っていることが確認できます．完全性関係はただの単位行列となるのでどこに挿入してもよく，式変形に便利です．完全性関係をマスター方程式の両辺に挿入すれば

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\cA}{\mathcal{A}}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\begin{align*}
\pd{}{t}\ket{f} &= \cA \ket{f}\\
\pd{}{t}\sum_\lambda \ket{\lambda}\bracket{\lambda}{f} &= \sum_\lambda \cA \ket{\lambda}\bracket{\lambda}{f}
\end{align*}
$$

となり，固有方程式からさらに

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\pd{}{t}\sum_\lambda \ket{\lambda}\bracket{\lambda}{f} = \sum_\lambda \lambda \ket{\lambda}\bracket{\lambda}{f}
$$

と展開できることがわかります．固有値の世界では固有値ごとに方程式をバラバラに分解できるというわけです．今の具体的なものにあてはめると，

$$
\newcommand{\lr}[1]{\left(#1\right)}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
&\pd{}{t} \lr{
(p_1 + p_2) \begin{pmatrix}
0.25\\
0.75
\end{pmatrix}
+ (0.75 p_1 - 0.25 p_2) \begin{pmatrix}
1\\
-1
\end{pmatrix}
} \\
&= 0 \times (p_1 + p_2) \begin{pmatrix}
0.25\\
0.75
\end{pmatrix}- 0.8 \times (0.75 p_1 - 0.25 p_2) \begin{pmatrix}
1\\
-1
\end{pmatrix}
\end{align*}
$$

と展開されます．固有値$${0}$$というのは確率の和が変化しないというところから必ず出てくるわけです．

分布の時間発展は，固有値ごとに解けば良いことから

$$
\begin{align*}
\begin{pmatrix}
p_1\\
p_2
\end{pmatrix}
&=
\begin{pmatrix}
0.25 & 0.25 \\
0.75 & 0.75
\end{pmatrix}
\begin{pmatrix}
p_1(0)\\
p_2(0)
\end{pmatrix}
+e^{-0.8 t} \begin{pmatrix}
0.75 & -0.25\\
-0.75 & 0.25
\end{pmatrix}
\begin{pmatrix}
p_1(0)\\
p_2(0)
\end{pmatrix}\\
&=
\begin{pmatrix}
0.25 \\
0.75
\end{pmatrix}
+e^{-0.8 t} \begin{pmatrix}
p_1(0) -0.25\\
p_2(0) - 0.75
\end{pmatrix}
\end{align*}
$$

となります．無限の時間が経つと，確率関数は，初期値がなんであっても，

$$
p_1(\infty) = 0.25,\ \ p_2(\infty) = 0.75
$$

つまり固有値$${0}$$に対応する固有ベクトルとなります．緩和時間とは平衡状態に達するまでの時間の尺度として用いられるもので、もうひとつの固有値である$${0.8}$$の逆数の$${1.25}$$が緩和時間になります．

今まで一匹のカエルについての確率密度を考えました．カエルたちが独立に動くとき，これは多数のカエルたちの分布の期待値と一致するので，これでカエルの分布の時間変化を考えたことにしてよいでしょう．

ただし，これは大数の法則という別の法則を使ったことになります．その証明も必要でしょうがそれはまたの機会に．

今度は多数のカエルの分布それ自体を確率変数として扱ってみましょう．（ここでカエルの分布と言っているのは確率密度のことではありません．カエルの分布が実際にどうなるかに対して確率密度を与えたい，つまり，ある瞬間に石１にカエルが１０匹いる確率はいくらか，というような問いに答えたいのです．）カエルの分布について期待値をとったら最初の考えで求めたものと一致するはずで，今度の考え方の方がより詳しいものを求めたいことになります．ある時刻で石１にいるカエルの数，石２にいるカエルの数をそれぞれ$${x_1(t), x_2(t)}$$と置き，このセットが確率変数になります．（といったものの，カエルの総数は変わらないので，石１にいるカエルの数のみ確率変数に考えれば十分ですが．）しかし，この場合事象の数はカエルの数に比例して大きくなるので，そのそれぞれに対して遷移速度を与えてマスター方程式を立てるのは大変です．この難しさは，マスター方程式の右辺が全状態に関する積分（和）になっていることからきているといえます．そこで，状態の変化は近い状態にしか起こらないことを仮定して，右辺を状態に関する微分の形に直せば，運動方程式を立てることができそうです．

ということで，そのための方法は次回考えましょう．右辺を状態の微分形で書いたマスター方程式のことをクラマース・モヤル（Kramers-Moyal）方程式といいます．特に，確率過程がガウス過程というもののときにはフォッカー・プランク（Fokker-Planck）方程式と呼ばれよく取り扱われます．

まとめ

マルコフ過程は過去の記憶によらない確率過程のことである．マルコフ過程は，時間の一階微分の形の方程式で確率密度の時間発展が記述される．とくに，遷移速度を用いて導かれるその微分方程式のことをマスター方程式といい，固有関数（固有ベクトル）を用いて解けることがある．