
マインスイーパー改造案集
どうも、最近なぜかマインスイーパーにハマっている108Hassiumです。
私が普段プレイしているのは以下のものです。
このMicrosoft Minesweeperには「Daily Challenges」というモードがあり、変則的なルールでマインスイーパーをプレイできます。

これらで遊んでいるうちに、新たな変則マインスイーパーやマインスイーパーを基にした別のゲームのアイディアがいくつか浮かんできたので記録しておきたいと思います。
※前例の有無や面白さは、特に記載がない限り確認・検証していません。
変則フィールド
まず紹介するのはこちら。

マス目の形が違うマインスイーパーです。
上の画像のものは、通常のマスを4分割した直角二等辺三角形が1つのマスになっています。
「改造案」と言いつつも、実は案だけではなく実際にプレイ可能なものがすでに完成しています。
#Processing
— 108Hassium (@1Hassium) April 7, 2023
マス目が三角形のマインスイーパーを作りました。 pic.twitter.com/D0XBPHPxMy
Twitterでこの動画を投稿した数日後、こんなツイートを発見しました。
Minesweeper, but on the new Einstein tiles pic.twitter.com/MRvcZtAQZQ
— Matt Henderson (@matthen2) April 9, 2023
最近発見されて大きく話題になった「1種類で非周期的にしか平面充填できない連結なタイル」を使ったマインスイーパーだそうです。
このように、隣接関係が定まっていればどんなフィールド上でもマインスイーパーができそうです。
というわけで、こんなものをつくりました。
#Processing
— 108Hassium (@1Hassium) April 13, 2023
盤面がランダムすぎるマインスイーパー pic.twitter.com/IP5nslcmpk
隣接関係さえあればいいのであれば、フィールドをタイル状に分割する必要もないのではないか、と考えました。
というわけで、点をランダムに(近すぎる点のペアが発生しないように)配置して、距離が一定以下の点のペアを隣接していると見做し、それぞれの点を1個のマスとすることでランダム盤面マインスイーパーが出来上がります。
ちなみに実際にプレイしてみたところ、自作のものはどちらも非常に難易度が高かったです。
まずランダム盤面の方ですが、マスの隣接関係がランダムなためマスごとに違った考え方の読みを要求されます。
非周期タイルの方でもマスの隣接関係が一定ではない(多分)ため、おそらく同様の難しさがあると予想できます。
なおにランダム盤面の方では「隣接するマスの見落としによる爆死」が多発したのですが、原因は単なる不注意だけでなく「黒背景+青線」という配色による視認性の悪さのせいでもあったのではないかと思います。
ちなみに、Twitterでは「盤面が立体的に見える」というような錯視現象を報告する人が複数見られました。

私は別にそのようには見えなかったのですが、長時間プレイすると激しい頭痛に襲われたので脳が何らかの誤作動を起こしていた可能性はありそうです。
三角タイルの方はどのマスも(周辺との隣接関係も含めて)同じ形になっているのですが、隣接するマスの数が多い(14個)ため複雑な読みが必要になります。
地雷の密度は1/8にしてあり、普通のマインスイーパーのEasyモード(10/81)とほとんど変わらないのですが、実際の難易度はExpert(密度は33/160≒1/5)と同レベルです。
もし隣接するマスの個数が多ければ多いほど難易度が上がるのであれば、全てのマスが等価(マス自体の形も周辺の形状もすべて同じ)という条件下では以下のタイリングを使ったものが一番難しくなりそうです。

また、以下のようなフィールドでの難易度も気になります。

隣接するマスの数は通常と同じく8マスですが、繋がり方が異なります。
通常のマインスイーパーにおけるマスの隣接関係はチェスのキングの駒(将棋の王将)の移動範囲と同じ形になっているのに対し、こちらはナイト(桂馬の全方向版)の移動範囲になっています。
ボードゲーム化
「地雷原将棋」は、将棋とマインスイーパーを組み合わせたデジタルボードゲームです。
マスにはランダムな位置に地雷が設置され、盤上にある自分の駒には「移動可能な位置にある地雷の個数」が表示されています。



※私は将棋には詳しくないので、実際のゲーム展開において画像のような盤面がどういう状況かは考えずに例を作っています。
駒の移動先に地雷があれば、そのマスは爆発します。(初期配置で地雷と駒が重なっていたり持ち駒を地雷の上に打った場合は爆発しない)
マスが爆発するとそのマスに移動した駒は爆死し、もし地雷の上にある駒を取ろうとした場合は移動してきた駒も元からいた駒も両方爆死します。(爆死した駒は相手の持ち駒にはならず、爆発したマスには他の駒は侵入できなくなる)
同様のアイディアはチェスにも適用可能ですが、あえて全然違う形式のボードゲームをマインスイーパーと組み合わせられないか考えてみました。
「爆散オセロ」は、オセロとマインスイーパーを組み合わせたデジタルボードゲームです。
地雷原将棋と同様に盤上にランダムに地雷が配置され、盤上にある自分の石には「隣接するマスにある地雷の個数」が表示されます。


地雷があるマスに石を置いた場合、通常のルールにおいてひっくり返される位置の石と新たに置いた石は盤面から除去され、石を置いた方ではないプレイヤーのものとなります。(地雷原将棋と同様、地雷があったマスには石を置けなくなる)
ペンシルパズル化
何だか物騒な話になってしまったので、次は地雷の出てこない平和なゲームを紹介します。
「No Mines」は、マインスイーパーから地雷の概念を除去したようなルールのペンシルパズル(数独やクロスワードのような、問題図に答えを直接書き込むパズル)です。
初期配置は以下のように「白マス」「黒マス」「数字の入ったマス」で構成された長方形で、マスに入った全ての数字が「そのマスに接しているマスに同じ数字が最大で何個入っているか」を表すように白マスを数字で埋めることが目的です。

※作問のコツが全く分からなかったので極小の問題しか作れませんでした。
ルールが少し複雑なので、具体例で補足します。

まずAのマスには、1が1個、2が2個、4が1個接しています。
よって、Aには個数の最大値である2が入ります。
同様に、Bには1が1個、2が4個、4が1個(黒マスは関係ない)接しているのでB=4になります。
私はペンシルパズルには詳しくないのでこのパズルが面白いのかはわかりませんが、どうやら作問の難易度がかなり高いようです。
ペンシルパズルの中には、「解答を先に作ってからその一部を消す」という手順により(面白さや解の唯一性を無視すれば)問題としての最低限の体裁は整うというものもあります。
しかしNo Minesの場合は、適当に数字を配置していくと大抵どこかで行き詰まり、修正すると別のところが矛盾し、という繰り返しに陥りやすいです。
私は以前こんな動画を投稿したのですが、実はこの動画の内容はNo Minesの作問を試みた際に思い付いた副産物です。
#cellularautomaton #セル・オートマトン
— 108Hassium (@1Hassium) March 25, 2023
マインスイーパーをプレイしてて思い付いたルール。 pic.twitter.com/bQ3bwm9Zmz
No Minesは、このセル・オートマトンで固定物体を作るゲームと考えることができます。
しかし動画を見てもらうとわかる通り、このセル・オートマトンの挙動はカオス的で、放置しても安定な構造が自然発生することはありませんでした。
ちなみに、最初に紹介した2つの例題の作成には別のセル・オートマトンの知識を利用しています。
B/S2というセル・オートマトンで固定物体を作り、生きたセルを2、死んだセルを黒マスに変換するとNo Minesの盤面として成立します。

先程の例題は、この方法で生成した盤面の黒マスのうちのいくつかを慎重に数字に置き換えることで作成しました。
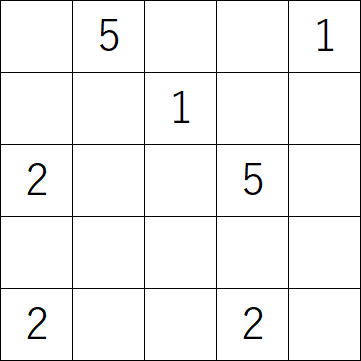
No Minesのバリエーションとしては、数字の意味を「何種類の数字が接しているか」に変えたものが考えられます。(以下、「No Mines II」)

例えば以下の盤面の真ん中のマスは、1、2、3の3種類の数字と接しているので3が入ります。

No Minesのような効果的っぽい作問方法(CAを利用するものとか)は見つかっていませんが、適当に数字を入れていって偶然盤面が成立することが結構あるので、結果的に作問難易度は若干低そうです。
あとペンシルパズル向きのルールではありませんが、「マスに入っている数字が『そのマスと色の違うマスが何個接しているか』を意味するように全てのマスを指定された色数で彩色する」という案もあります。
例えば以下の盤面では、真ん中のマスに接しているのは赤が2つ、緑と青が3つずつなので、赤で塗れば違う色が6マス接することになり数字と一致します。

