
【3】ちょっと珍しい有理関数
どうも、108Hassiumです。
この記事は周期発散関数に関する記事の第3弾です。
☟前回
☟前々回
穴の正体
前回と前々回の記事では、「周期発散関数のジュリア集合の穴の形状」と「普通のジュリア集合の収束領域の形状」の関連性について触れました。

3周期ジュリア集合の収束領域の形状と似ている
また、以下の記事では3周期発散関数の「新種」について触れ、それもまた収束領域と対応付けられるという話をしました。
実は、これ系の話題の本質のような話が以下の記事に出てきています。
この記事では、以下のような話が出てきます。
$${f(z)}$$と$${g(z)}$$について、$${g(z)=h^{-1}(f(h(z)))}$$が成り立つような$${h(z)}$$が存在するとき、「$${f(z)}$$と$${g(z)}$$は位相共役である」という。
$${f(z)}$$と$${g(z)}$$が位相共役である場合、$${f(z)}$$と$${g(z)}$$のジュリア集合は発散・収束の速度、領域の繋がり方、尖り具合や曲がり具合といった様々な特徴が一致する。
※本来は$${h(z)}$$と$${h^{-1}(z)}$$が連続写像でないと位相共役とは言えないらしいですが、面倒なので今回は気にしないことにします。
そして、$${a(z+\frac{1}{z})+b}$$という形の有理関数の中に$${\frac{c}{z^2-1}+1}$$(2周期発散関数)と位相共役なものが存在することを紹介しました。

上の画像を見ると確かに2周期発散関数のジュリア集合にそっくりなのですが、2周期発散関数における発散領域に見える部分は実は2周期の収束領域になっています。
どうやら、$${n}$$周期発散関数$${f(z)}$$に対して$${h(z)}$$を上手く選ぶことで、$${h^{-1}(f(h(z)))}$$を「$${f(z)}$$のジュリア集合とそっくりだが、穴の部分が$${n}$$周期の収束領域に置き換わったジュリア集合を持つ関数」にできるようです。
ピンとこない人もいると思うので、別の例を挙げます。
まず、$${-\frac{c^3-c^2-c+1}{z^2-1}+c}$$という3周期発散関数があります。

ジュリア集合はこんな感じで、$${c→1→\infty→c}$$という発散サイクルを持ちます。

この関数を$${f(z)}$$とし、さらに$${h(z)=\frac{1}{z+1}}$$として、$${h^{-1}(f(h(z)))}$$のジュリア集合を描画してみるとこうなります。

白っぽい領域が元のジュリア集合の収束領域に対応する領域で、黒いのは$${\frac{1}{c}-1→0→-1→\frac{1}{c}-1}$$という3周期のサイクルに対応する収束領域です。
この$${\frac{1}{c}-1→0→-1→\frac{1}{c}-1}$$というサイクルは元の関数の発散サイクルの値に$${h^{-1}(z)}$$を適用した値でできており、$${f(z)}$$の発散領域が共役変換により収束領域に変換されたことを表しています。
また、これと逆の操作を行うこともできます。
まず、$${f(z)=\frac{2}{z^2-1}+1.3+1.46i}$$のジュリア集合はこんな形をしています。

白い領域が$${z_0=0}$$の収束先である6周期の領域で、その他のカラフルな領域が$${z_0=1.3+1.46i}$$に対応する領域です。
$${z_0=0}$$の収束先である6周期サイクルの中身の1つを$${d}$$とし、$${h(z)=\frac{1}{z}+d}$$とすると$${h^{-1}(f(h(z)))}$$のジュリア集合はこうなります。

6周期の収束領域が発散領域になり、$${h^{-1}(f(h(z)))}$$は6周期発散関数になりました。
これらが表すのは、周期発散関数の穴と収束領域は実質ほとんど同じような存在であるということです。
3周期発散関数の穴が(少なくとも)3種類あるのは3周期の収束領域が3種類あるのと同じことですし、より一般に収束領域がある特徴を持てば似た特徴の穴を持つ周期発散関数が存在するはずです。
ところで、周期発散関数の見た目の特徴と言えばもう一つ別の話がありました。
周期発散関数の発散領域の模様には$${\frac{c}{z^2-1}+1}$$や$${-\frac{c^3-c^2-c+1}{z^2-1}+c}$$のような網目状のものだけでなく糸状のものがあり、そういった特徴が「極の位数」と結びついているのではないか、という話です。

位数$${n}$$の極は共役変換により多重度$${n-1}$$の臨界点に変化させられるのですが、多重度$${n-1}$$の臨界点があることと収束領域の境界線が糸状になることに関係があるのかはよくわかっていません。
1次型3周期発散関数
突然ですが、新たな用語を一つ定義します。
$${n}$$周期発散関数のうち、$${f^n(z)}$$の次数が1になるようなものを「1次型」の$${n}$$周期発散関数と呼ぶことにします。
前々回の記事では周期発散関数の定義に1次型のものを含んでおらず、前回の記事で定義を拡張して1次型を含めるように変更し、そのうえで「1次型の3周期発散関数を見つけるのは難しい」という話をしました。
そして、つい最近になってようやく1次型3周期発散関数の無限族を簡単に見つける方法を発見したので紹介したいと思います。
まず、$${f(z)=a(\frac{1}{z}-\frac{c^2}{z-b})+d}$$と置きます。
この形の関数には、以下のような特徴があります。
式変形すると分母が2次になる。
臨界点が2個あり、それらが有理式で表せる。
次に、$${f(z)}$$が以下のような発散サイクルを持つように係数を決めます。
$${f(b)=\infty}$$
$${f(\infty)=d}$$
$${f(d)=b}$$
上2つの式は特別な条件が無い限り勝手に満たされるので、最後の方程式だけを解きます。
$${f(d)=a(\frac{1}{d}-\frac{c^2}{d-b})+d\\=\frac{a(d-b-c^2d)}{d(d-b)}+d\\=b}$$
$${a}$$について解けそうな見た目になったので、解きます。
$${a=\frac{d(d-b)^2}{c^2d-d+b}}$$
これを$${f(z)}$$に反映させてDesmosでグラフを描画すると、ちゃんと1次型3周期発散関数になっていることが確認できます。
$${b,c,d}$$を変化させると、$${f^3(z)}$$のグラフの形状は以下のように変化するようでした。
$${b}$$を動かすと、$${|b|}$$が小さい場合傾きは不規則に変化するが、ある程度大きくなると0に収束していく。
$${c}$$を動かすと、$${b,d}$$の値との組み合わせ次第で1次型でなくなる値がいくつか存在することがあるが、$${c=\pm1}$$だと$${b,d}$$に関係なく必ず1次型ではなくなる。
$${d}$$を動かすと、$${b}$$を動かしたときと同様に傾きが不規則に変化するが、$${|d|→\infty}$$での傾きの収束先は$${b,c}$$によって変化する(1を下回ることはなさそう)っぽい。
というわけで、とりあえず$${b=1,c=2}$$として、マンデルブロ集合を描画するとこんな感じになりました。


前回紹介したものと似たような形になりました。
$${c}$$を3に変えるとこんな感じになります。


ちなみに、以前紹介した$${\frac{c+1}{5c+4}(\frac{1}{z}-\frac{4c}{cz-2c-1})+\frac{1}{c}+1}$$という関数は、途中までは同じ方法を使って見つけたものです。

$${f(d)=b}$$を$${a}$$について解いた後、$${a}$$を簡単な式にするために$${b=d+1}$$としています。
そして$${c=2}$$にするのは同じですが、最後に残った$${d}$$をそのまま$${c}$$(この$${c}$$は$${c=2}$$の$${c}$$とは別)に書き換えずに$${d=\frac{1}{c}+1}$$と書き換えます。
この書き換えにより、無限遠までずっと伸びている形のマンデルブロ集合が有限のサイズに収まるようになります。
ところで、1次型の周期発散関数で遊ぶには$${f^n(z)}$$の傾き(無限遠点での微分係数)を気にする必要があります。
2周期の場合は傾きを手計算で求めることができ、3周期の場合もグラフを見て大きさを評価できたのですが、一方で3周期の場合の傾きの厳密値を求められるようなケースはまだ見つかっていません。
前回紹介した数列を用いれば理論上は求められるのですが、実際に試したところあまりにも面倒臭すぎるので断念しました。
というわけで、もう少しマシ(に見えるけど実際は上手くいかない)な方法を紹介します。
まず、$${f^3(z)}$$を合成関数の微分公式だけで展開します。
$${f(f(f(z)))'=f'(f(f(z)))×(f(f(z))')\\=f'(f(f(z)))×f'(f(z))×f'(z)}$$
展開し終わったら、$${f(z)}$$を求めるのに使った発散サイクルの式を使用して$${f(f(f(\infty)))'}$$を計算します。
※$${f(z)}$$は0次の有理関数なので、$${f'(\infty)=0}$$です。
$${f(f(f(\infty)))'\\=f'(f(f(\infty)))×f'(f(\infty))×f'(\infty)\\=f'(f(d))×f'(d)×0\\=f'(b)×f'(d)×0\\=\infty×f'(d)×0}$$
$${f'(d)}$$は有限の値になりますが、残りの部分が$${\infty×0}$$なのでこれ以上計算できません。
$${\displaystyle{\lim_{z→\infty}}f'(z)}$$の収束と$${\displaystyle{\lim_{z→\infty}}f'(f(f(z)))}$$の発散の速度がそれぞれ評価できればいいのですが、私には無理でした。
5周期発散関数を求めて
前回の記事では5周期発散関数について「求められそうな方法を発見したが、面倒臭いので試してはいない」と書いたのですが、実は前回紹介した方法には欠陥がありました。
前回の記事の投稿後に色々と改善策を探したのですが、未だに「臨界点が有理式で表せる有理係数5周期発散関数」の具体例は見つけられていません。
※先に紹介した共役変換を利用した方法では係数が有理式にならない(例として使用した画像では近似値を使用)ので論外です。
というわけで、失敗したアプローチの例をいくつか紹介します。
まず、前回紹介した「ラグランジュ補完みたいな方法」を試します。
まず、$${f(z)=\frac{d(z-g)(z-h)+j(z-g)(z-k)+m(z-h)(z-k)}{(z-a)(z-b)(z-c)}+g}$$とします。
この場合、以下のような発散サイクルを持たせられそうです。
$${f(a)=\infty}$$
$${f(\infty)=g}$$
$${f(g)=h}$$
$${f(h)=k}$$
$${f(k)=a}$$
最初の2本の式は自然に成り立つので、下の3本を連立方程式として解きます。
$${\begin{cases}\frac{m(g-h)(g-k)}{(g-a)(g-b)(g-c)}+g=h\\\frac{j(h-g)(h-k)}{(h-a)(h-b)(h-c)}+g=k\\\frac{d(k-g)(k-h)}{(k-a)(k-b)(k-c)}+g=a\end{cases}}$$
$${d}$$、$${j}$$、$${m}$$について解くとこうなります。
$${d=\frac{(a-g)(k-a)(k-b)(k-c)}{(k-g)(k-h)}}$$
$${j=\frac{(k-g)(h-a)(h-b)(h-c)}{(h-g)(h-k)}}$$
$${m=-\frac{(g-a)(g-b)(g-c)}{g-k}}$$
次に、臨界点に関する条件を決めるために$${f(z)}$$を微分します。
$${f(z)'=(\frac{(d+j+m)z^2-(dh+dg+jg+jk+mh+mk)z+dgh+jgk+mhk}{z^3-(a+b+c)z^2+(ab+bc+ac)z-abc}+g)'\\=\frac{(2(d+j+m)z-dh-dg-jg-jk-mh-mk)(z-a)(z-b)(z-c)-((d+j+m)z^2-(dh+dg+jg+jk+mh+mk)z+dgh+jgk+mhk)(3z^2-2(a+b+c)z+ab+bc+ac)}{(z^3-(a+b+c)z^2+(ab+bc+ac)z-abc)^2}}$$
はい、もう無理です。
これを整理して分母=0(4次方程式)の解が有理式になるような条件を見つけるとか、正気の沙汰ではありません。
というわけで、もう少しマシな方法を考えました。
まず、$${f(z)=\frac{1}{(z-a)(b(z-c)(z-d)+g(z-d)(z-h)+j(z-h)(z-c))}+c}$$と置きます。
この場合、以下のような発散サイクルを持たせられそうです。
$${f(a)=\infty}$$
$${f(\infty)=c}$$
$${f(c)=d}$$
$${f(d)=h}$$
$${f(h)=a}$$
$${\begin{cases}\frac{1}{g(c-a)(c-d)(c-h)}+c=d\\\frac{1}{j(d-a)(d-h)(d-c)}+c=h\\\frac{1}{b(h-a)(h-c)(h-d)}+c=a\end{cases}}$$
$${b=\frac{1}{(a-c)(h-a)(h-c)(h-d)}}$$
$${j=\frac{1}{(h-c)(d-a)(d-h)(d-c)}}$$
$${g=-\frac{1}{(c-a)(c-d)^2(c-h)}}$$
$${f(z)}$$を微分します。
$${f'(z)=\frac{b(z-c)(z-d)+g(z-d)(z-h)+j(z-h)(z-c)+(z-a)(b(2z-c-d)+g(2z-d-h)+j(2z-h-c))}{(z-a)^2(b(z-c)(z-d)+g(z-d)(z-h)+j(z-h)(z-c))^2}\\=\frac{(b+g+j)z^2-(bc+bd+gd+gh+jh+jc)z+bcd+gdh+jhc+(z-a)((2b+2g+2j)z-bc-bd-gd-gh-jh-jc)}{(z-a)^2(b(z-c)(z-d)+g(z-d)(z-h)+j(z-h)(z-c))^2}\\=\frac{3(b+g+j)z^2-2(bc+bd+gd+gh+jh+jc+ab+ag+aj)z+bcd+gdh+jhc-abc-abd-agd-agh-ajh-ajc}{(z-a)^2(b(z-c)(z-d)+g(z-d)(z-h)+j(z-h)(z-c))^2}}$$
めちゃくちゃ長い式になりましたが、$${bcd+gdh+jhc-abc-abd-agd-agh-ajh-ajc=0}$$が成り立てば分子=0の解の一つが$${z=0}$$になり、残りの解も有理式で表せるようになりそうです。
$${bcd+gdh+jhc-abc-abd-agd-agh-ajh-ajc\\=(cd-ac-ad)b+(dh-ad-ah)g+(hc-ah-ac)j\\=\frac{(cd-ac-ad)}{(a-c)(h-a)(h-c)(h-d)}-\frac{(dh-ad-ah)}{(c-a)(c-d)^2(c-h)}+\frac{(hc-ah-ac)}{(h-c)(d-a)(d-h)(d-c)}=0}$$
分母の次数を下げるために、$${d=c-k}$$、$${h=c-m}$$と置いてみます。
$${\frac{(cd-ac-ad)}{(a-c)(h-a)(h-c)(h-d)}-\frac{(dh-ad-ah)}{(c-a)(c-d)^2(c-h)}+\frac{(hc-ah-ac)}{(h-c)(d-a)(d-h)(d-c)}\\=\frac{c(c-k)-ac-a(c-k)}{(a-c)(c-m-a)(c-m-c)(c-m-c+k)}-\frac{(c-k)(c-m)-a(c-k)-a(c-m)}{(c-a)(c-c+k)^2(c-c+m)}+\frac{(c-m)c-a(c-m)-ac}{(c-m-c)(c-k-a)(c-k-c+m)(c-k-c)}\\=-\frac{c^2-ck-2ac+ak}{m(k-m)(a-c)(c-a-m)}-\frac{c^2-cm-ck+km-2ac+ak+am}{k^2m(c-a)}+\frac{c^2-cm-2ac+am}{km(c-a-k)(m-k)}=0}$$
分母を払って$${a}$$と$${c}$$の2次式になればパラメータ解が求められそうなのですが、どう見ても3次以上になりそうです。
Desmosで確認してみたところ、こうなりました。
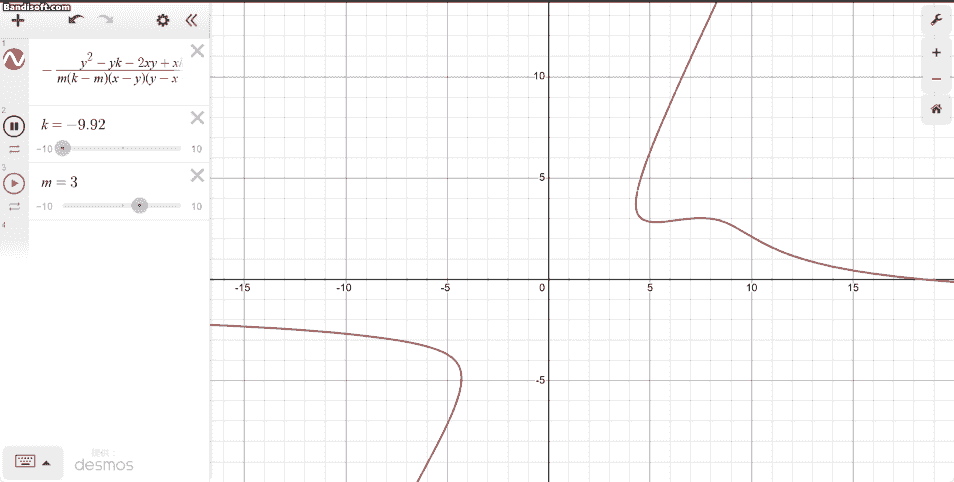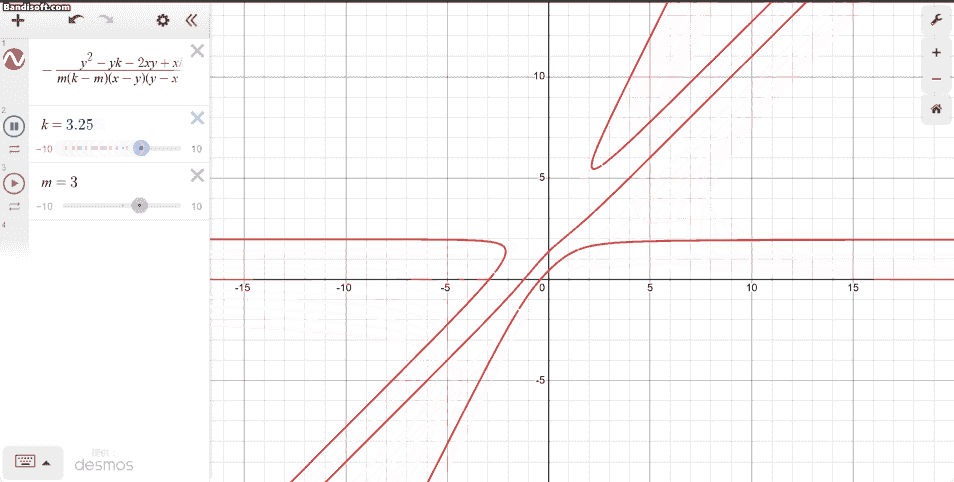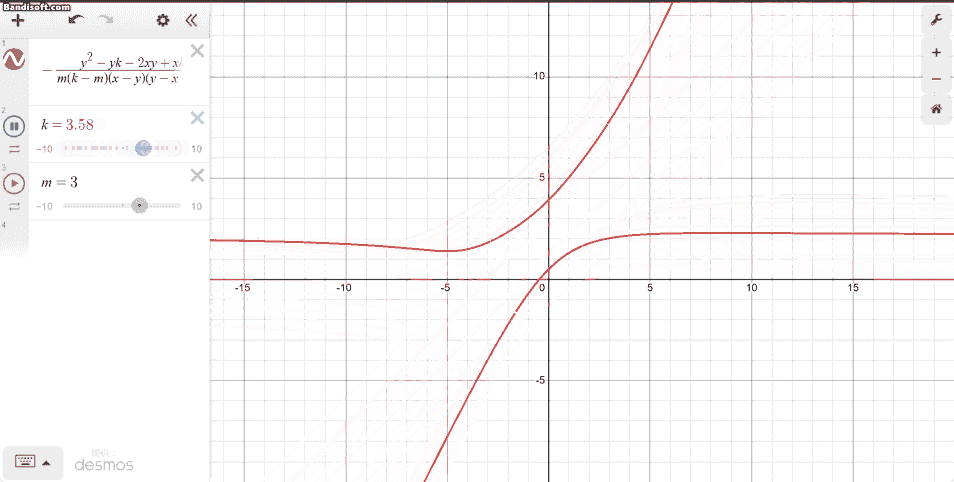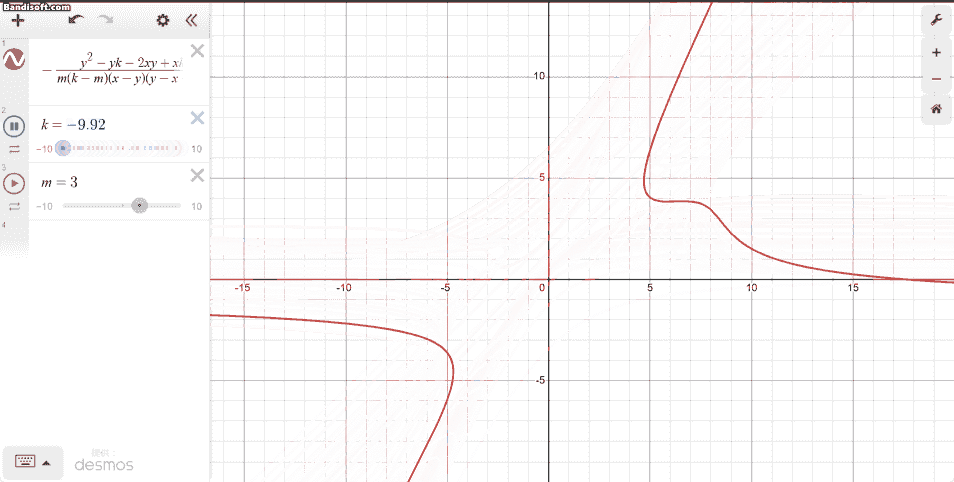
いかにもどうしようもなさそうな感じが見て取れます。
次に、$${d=kc}$$、$${h=mc}$$という変換を試してみます。
$${\frac{cd-ac-ad}{(a-c)(h-a)(h-c)(h-d)}-\frac{dh-ad-ah}{(c-a)(c-d)^2(c-h)}+\frac{hc-ah-ac}{(h-c)(d-a)(d-h)(d-c)}\\=\frac{kc^2-ac-kac}{(a-c)(mc-a)(mc-c)(mc-kc)}-\frac{kmc^2-kac-mac}{(c-a)(c-kc)^2(c-mc)}+\frac{mc^2-mac-ac}{(mc-c)(kc-a)(kc-mc)(kc-c)}\\=\frac{kc-a-ka}{c(a-c)(mc-a)(m-1)(m-k)}-\frac{kmc-ka-ma}{c^2(c-a)(1-k)^2(1-m)}+\frac{mc-ma-a}{c^2(m-1)(kc-a)(k-m)(k-1)}}$$
こっちもダメそうです。
ちなみに$${d=c-k}$$や$${d=kc}$$という式はどこから来たのかというと、元は$${b+g+j=0}$$という方程式を解こうとしていた時に思い付いた手法でした。
$${b+g+j=0}$$が成り立つと$${f'(z)}$$の分子の次数が下がるのですが、実際に解いてみると$${a}$$と$${c}$$の2次式に帰着させることはできるもののそこから大どんでん返しが発生して結局パラメータ解は求りませんでした。
また、そもそも$${b+g+j=0}$$が成り立つと$${f(z)}$$の分母の次数が2次に下がってしまい、分母を3次にした意味がなくなってしまいます。
分母が2次の場合も色々と試行錯誤して、ようやく解に辿り着いたと思いきや$${f^5(z)=z}$$になってしまった、というオチを踏んでしまって挫折しました。
