
今週のフラクタル51 ((z+0.02i/z)^3+c)
どうも、108Hassiumです。
今回は$${(z+\frac{0.02i}{z})^3+c}$$に関するフラクタル図形をお届けします。
(z+0.02i/z)^3+c


$${(z+\frac{0.02i}{z})^3+c}$$は$${z^3+c}$$を基にした摂動系の関数で、臨界点は±0.1±0.1i(複号任意)の4点で、その内0.1-0.1iと-0.1+0.1iの多重度が2、残りの2点が1です。
マンデルブロ集合の形状は、多重度2の初期値のものが全く同じ形かつ点対象で、$${z_0=0.1+0.1i}$$のものは非対称で$${z_0=-0.1-0.1i}$$は$${z_0=0.1+0.1i}$$のものを180度回転させた形になるようでした。
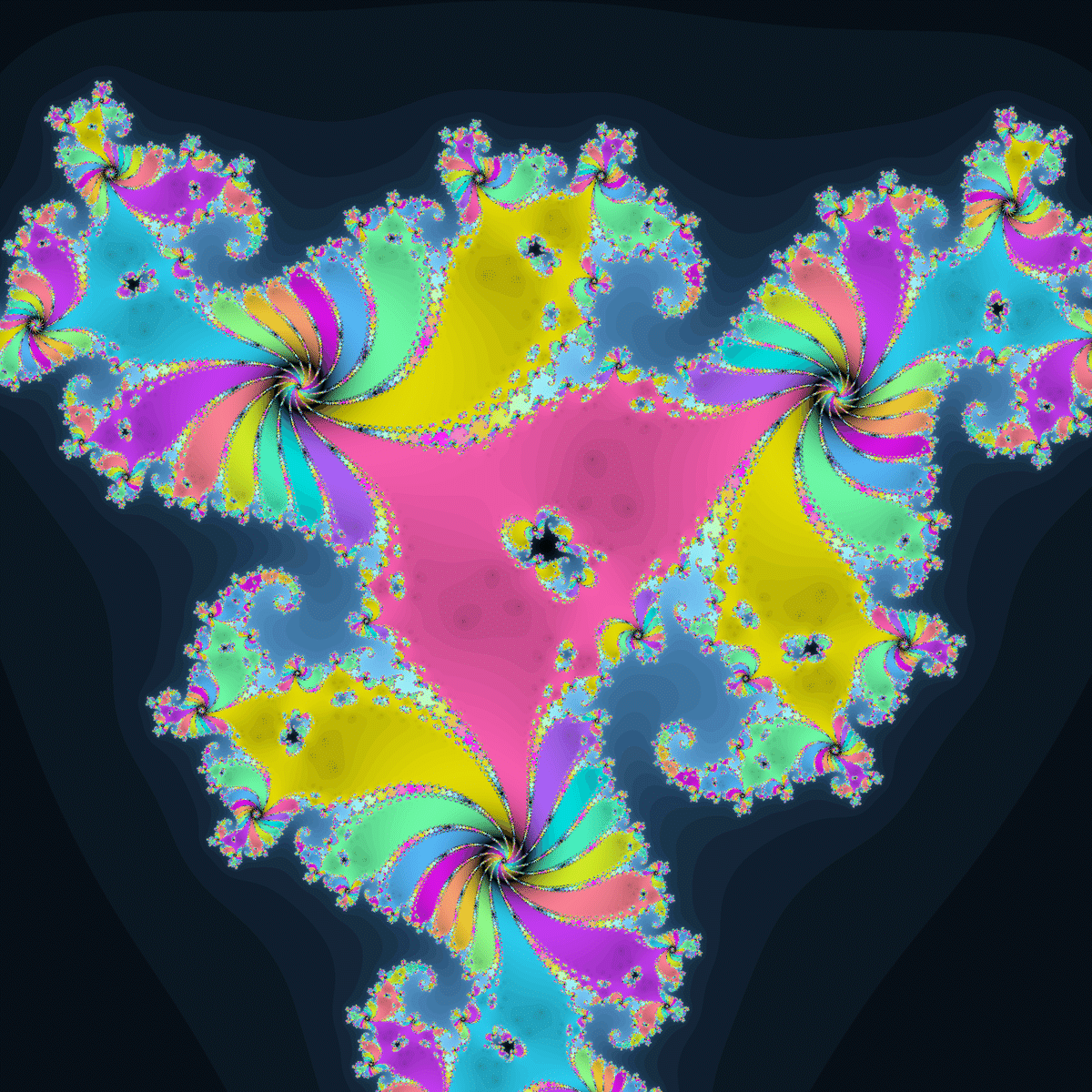




いかにも摂動系の関数っぽい見た目のジュリア集合です。










2種類の吸引的サイクルが存在するジュリア集合です。(3種類のものは見つかりませんでした)






いつものです。
