
今週のフラクタル61 (c(1/3(z-0.01/(z+0.2i))^3-(z-0.01/(z+0.2i))^2+4/3)-0.1i)
どうも、108Hassiumです。
今回は$${c\left(\frac{1}{3}\left(z-\frac{0.01}{z+0.2i}\right)^3-\left(z-\frac{0.01}{z+0.2i}\right)^2+\frac{4}{3}\right)-0.1i}$$に関するフラクタル図形をお届けします。
c(1/3(z-0.01/(z+0.2i))^3-(z-0.01/(z+0.2i))^2+4/3)-0.1i

$${c\left(\frac{1}{3}\left(z-\frac{0.01}{z+0.2i}\right)^3-\left(z-\frac{0.01}{z+0.2i}\right)^2+\frac{4}{3}\right)-0.1i}$$(以下、$${f(z)}$$)は$${c(\frac{z^3}{3}-z^2+\frac{4}{3})}$$を基にした摂動系の関数です。
$${c(\frac{z^3}{3}-z^2+\frac{4}{3})}$$の臨界点は$${z=0,2}$$の2点ですが、$${c(\frac{2^3}{3}-2^2+\frac{4}{3})=0}$$なので、$${c(\frac{z^3}{3}-z^2)+2}$$や$${c(2z^3-3z^2)+1}$$、$${c(2z^3-3z^2+1)}$$と同じような「臨界点が実質1個しかないと見做せる3次関数」です。
※☟$${c(\frac{z^3}{3}-z^2)+2}$$が出てくる記事
※☟$${c(2z^3-3z^2)+1}$$と$${c(2z^3-3z^2+1)}$$が出てくる記事

$${c\left(\frac{1}{3}\left(z-\frac{0.01}{z+0.2i}\right)^3-\left(z-\frac{0.01}{z+0.2i}\right)^2+\frac{4}{3}\right)-0.1i}$$の臨界点は、以下の4点です。
$${z=-0.3i}$$
$${z=-0.1i}$$(多重度3)
$${z-\frac{0.01}{z+0.2i}=2}$$の解(2点)
このうち最後の2点について$${f(z)}$$を計算すると$${-0.1i}$$になるので、$${c(\frac{z^3}{3}-z^2+\frac{4}{3})}$$の臨界点が実質1個しかないのと同様に$${f(z)}$$の臨界点は実質$${z=-0.1i,-0.3i}$$の2点しかないと見做すことができます。




ジュリア集合には「7重臨界点を持つ関数っぽい収束領域」がよく見られ、「3重臨界点を持つ関数っぽい収束領域」もたまに現れます。



いかにも摂動系の関数っぽい見た目のジュリア集合です。







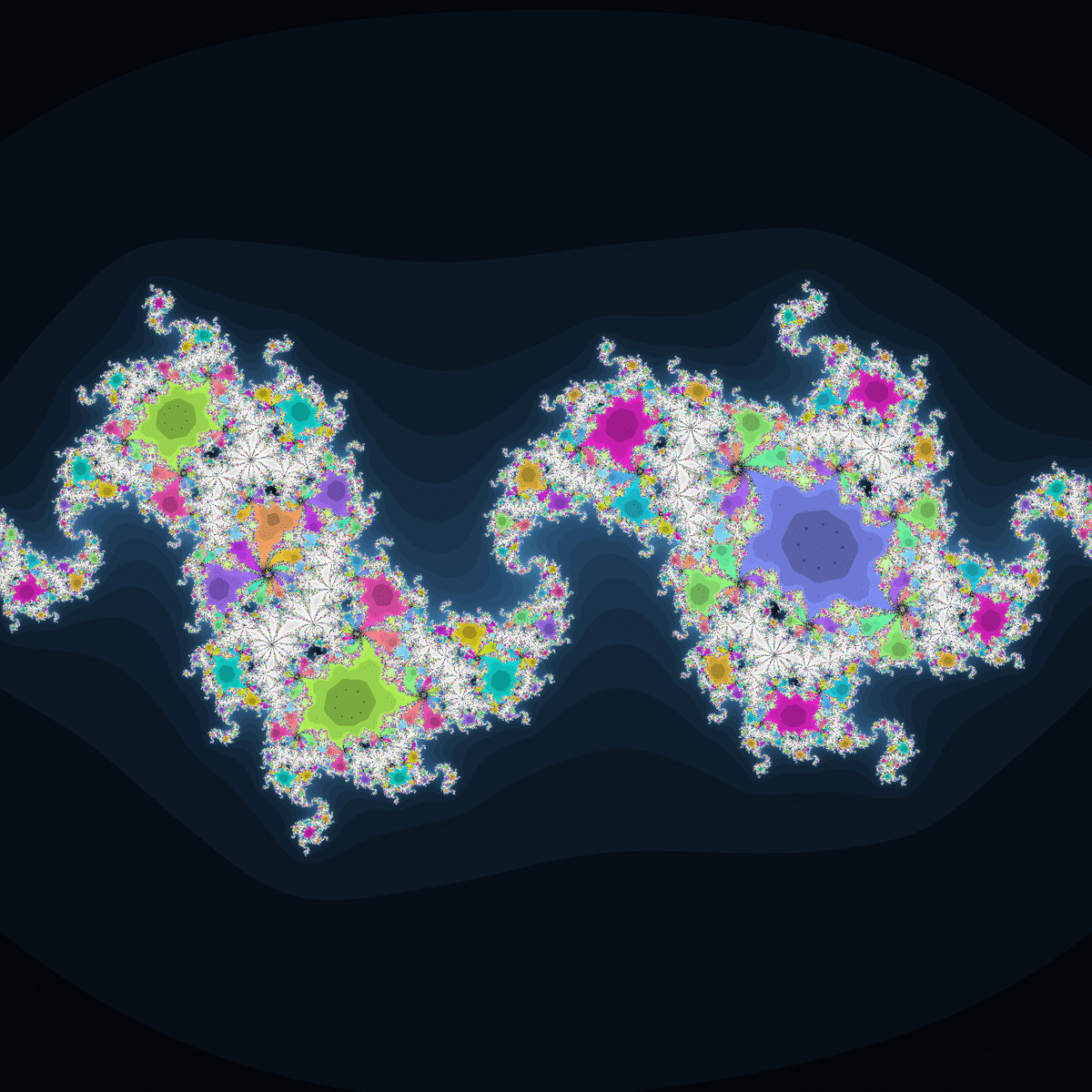

白領域のあるジュリア集合です。





いつものです。
