
ちょっと珍しい3次関数
どうも、108Hassiumです。
以下の記事では、ちょっと珍しい性質を持つ3次関数として$${f(z)=c(\frac{z^3}{3}-z^2)+2}$$という関数を取り上げています。
この関数の臨界点は0と2の2個がありますが、$${f(0)=2}$$なのでマンデルブロ集合やジュリア集合を描画する際には臨界点は1個しかないものとして扱えます。
先程の記事では「臨界点が実質1個しかないと見做せる3次関数」の例を他にもいくつか挙げていましたが、この記事ではそれぞれの例に対応するマンデルブロ集合やジュリア集合を紹介したいと思います。
なお、今回は先ほどの記事で上げた例に合わせて$${f(z)=c(2z^3-3z^2)+d}$$という形の3次関数を扱います。
この形の関数を使うのは
臨界点が0と1
係数がかなりシンプル
・・・等の理由によるものです。
「この形を標準形としてもいいのか?」という話は、以下の記事の最後の方で触れているので興味のある方は読んでみてください。
f(0)=0
※今までの記事ではマンデルブロ集合の生成に使う関数は$${z}$$と$${c}$$の2変数関数であることがわかるように$${f(z,c)}$$という形で書いていましたが、今回は諸事情により1変数関数で書きます。
$${f(0)=0}$$が成り立つと、マンデルブロ集合の描画に使う数列$${z_{n+1}=f(z_n)}$$は$${z_0=0}$$とするとずっと0のまま変動しなくなります。
$${f(z)=c(2z^3-3z^2)+d}$$に0を代入すると$${d}$$になるので、$${d=0}$$、つまり$${f(z)=c(2z^3-3z^2)}$$とすれば$${f(0)=0}$$になります。

中央にジュリア集合のような凹凸のある収束領域があり、左側の尖った部分の先に$${z^2+c}$$のマンデルブロ集合に似た領域があります。
収束領域の内側は収束速度に応じて彩色してあり、収束が遅ければ遅いほど明るい色になるのですが、中央の領域は収束がめちゃくちゃ速いのかほぼ真っ黒になっています。

$${z_0=0}$$の場合、$${c}$$の値に関係なく常に0に収束するのでこうなります。
ジュリア集合はこんな形です。


マンデルブロ集合と同様、0に収束する真っ黒い領域が現れます。
f(0)=1
$${f(0)=1}$$となると、$${z_0=0}$$の数列が$${z_0=1}$$の数列に合流するので$${c(\frac{z^3}{3}-z^2)+2}$$と同じように臨界点が1個であるかのように扱えます。
導出手順は先ほどと同じで、$${f(0)=1}$$を$${d}$$について解くことで$${f(z)=c(2z^3-3z^2)+1}$$が求まります。

$${c(\frac{z^3}{3}-z^2)+2}$$と同じ形になりました。

ジュリア集合も同様に、$${z^4+c}$$のような四角い形が現れます。
f(1)=0
$${f(1)=0}$$でも、$${f(0)=1}$$と同じように数列の合流が起きます。
$${f(1)=-c+d}$$なので$${d=c}$$となり、$${f(z)=c(2z^3-3z^2)+c}$$となりますが、さらに$${c(2z^3-3z^2+1)}$$と変形することもできます。
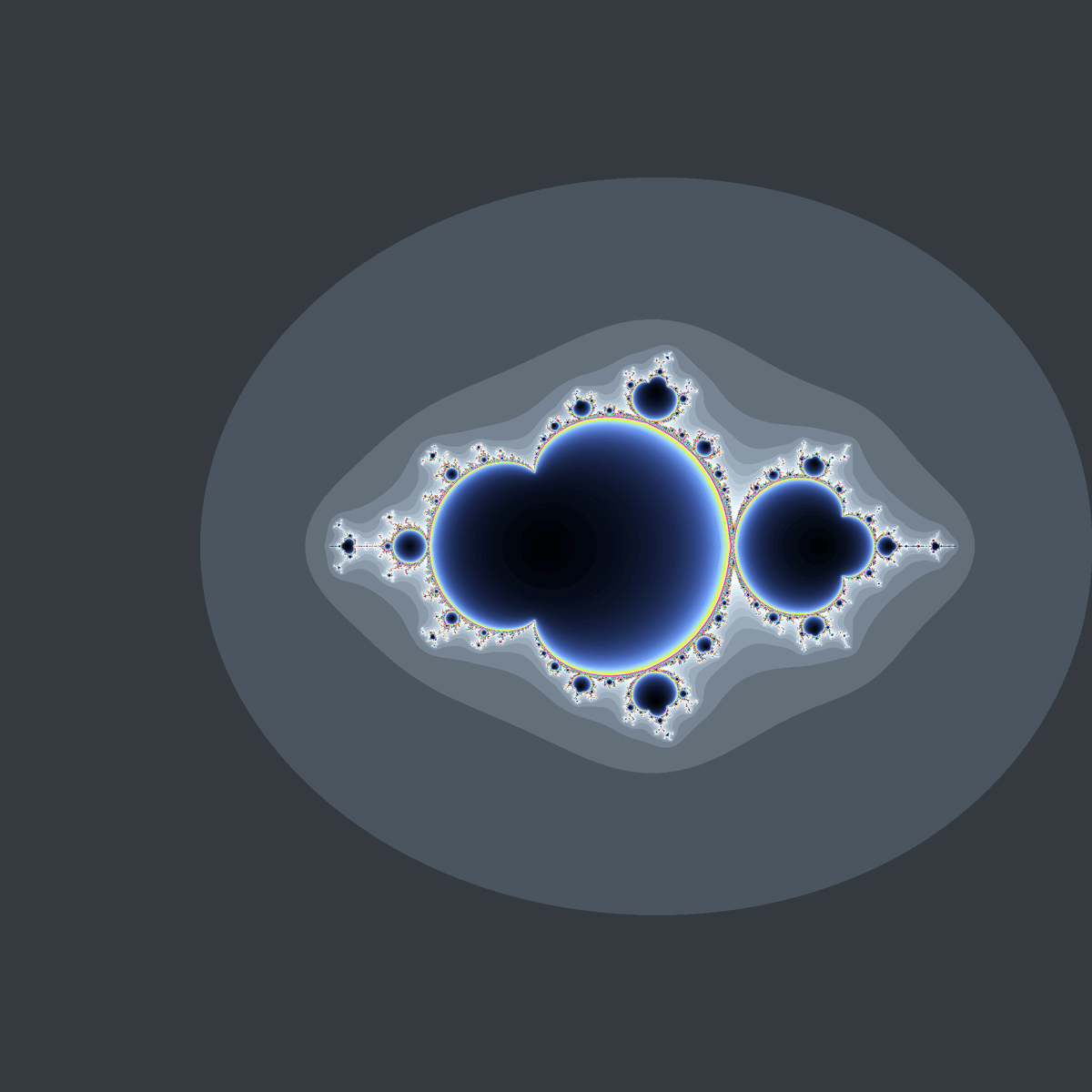
マンデルブロ集合の形状も、$${f(0)=1}$$のときと同じになってしまうようです。
f(1)=1
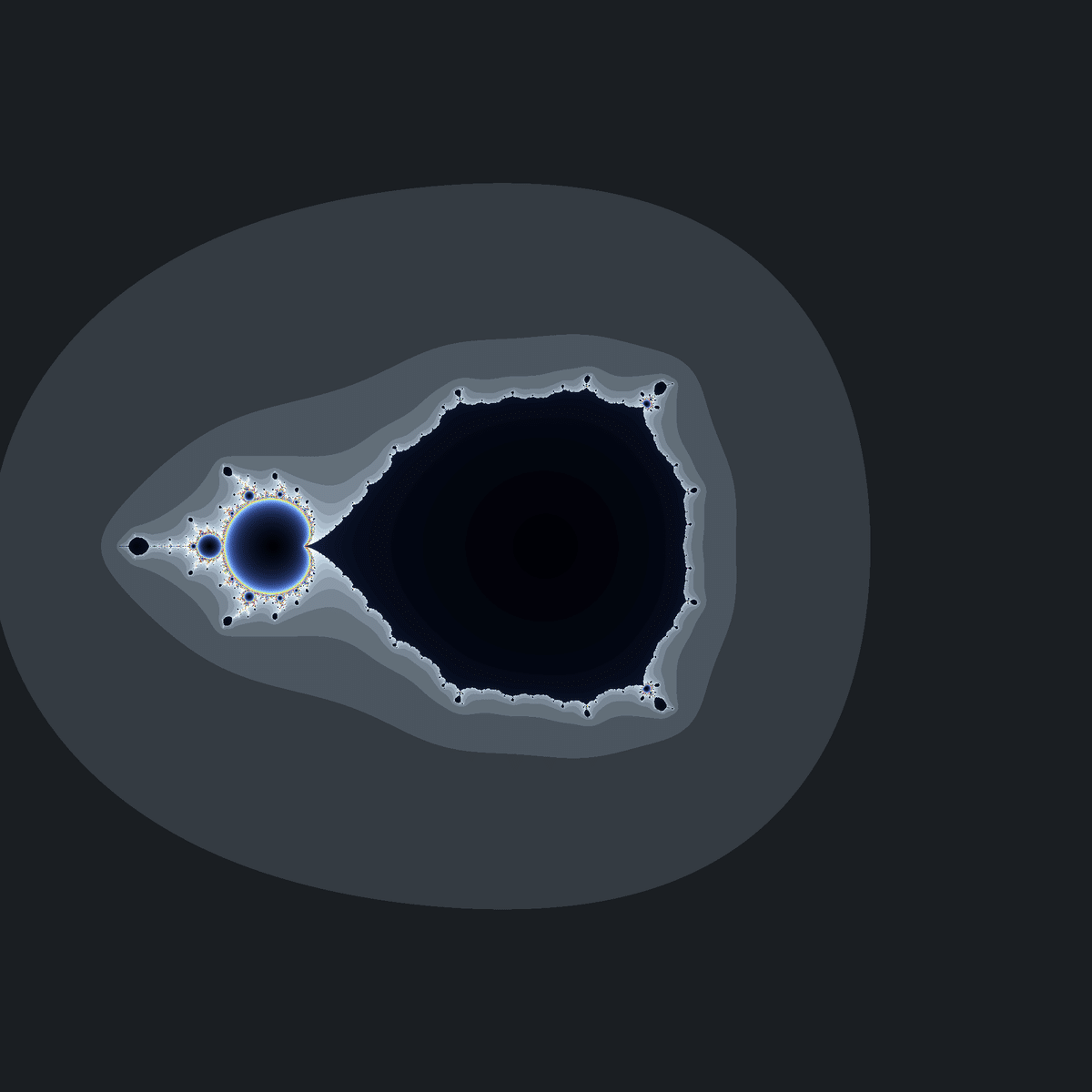
どうやら「$${f(0)=0}$$と$${f(1)=1}$$」や「$${f(0)=1}$$と$${f(1)=0}$$」のように0と1を入れ替えた方程式から得られるマンデルブロ集合(ジュリア集合も)は、同じ形になるようです。
f(0)=f(1)
$${f(0)=d}$$、$${f(1)=-c+d}$$なので$${f(0)=f(1)}$$の解は$${c=0}$$なのですが、そうなるともはや3次関数ではなくなるので「解無し」とします。
どうやら3次関数$${f(z)}$$の臨界点$${c_1}$$と$${c_2}$$について、$${c_1\neq c_2}$$ならば必ず$${f(c_1)\neq f(c_2)}$$になるようです。
実は3次関数の標準形として$${f(z)=c(2z^3-3z^2)+d}$$を選ぶと、$${z^3+c}$$や$${c(z^3-1)}$$のような「臨界点が2重解になる3次関数」だけを取りこぼしてしまうことになります。
なお、臨界点が2重解である$${z^3+c}$$や$${c(z^3-1)}$$は、「臨界点が1個しかないと見做せる3次関数」なので一応画像を載せておきます。


ジュリア集合は以下の記事内で見られます。
f(f(0))=0
$${f(f(0))=c(2d^3-3d^2)+d}$$となるため、$${f(f(0))=0}$$を$${d}$$について解くのは困難です。
なので$${d}$$ではなく$${c}$$について解き、解いた後で$${c}$$と$${d}$$を入れ替えることで$${f(z)=-\frac{1}{2c^2-3c}(2z^3-3z^2)+c}$$という関数を得られます。
※この「変数の入れ替え」は数学的にはちょっとまずい操作なのですが、細かいことが気になる人は「まず最初に$${f(z)=d(2z^3-3z^2)+c}$$と置く」などの小細工で回避できるので各自で計算し直して納得してください。

$${c}$$についての分数関数になったため全体像がかなり変わった形になりましたが、細部をよく見ると$${f(0)=0}$$の$${c(2z^3-3z^2)}$$と似ています。
暗い色の収束領域(0を含む2周期サイクルに収束する領域)にはジュリア集合のような凹凸があり、右半分には$${z^2+c}$$のマンデルブロ集合に似た形のケツに暗い色の領域が刺さっています。
大きく違うのは左半分が2周期のジュリア集合みたいな形になっていることと、非自明なサイクルに収束する領域のうち一番大きいものが首の部分で暗い色の領域と繋がっていることです。
ジュリア集合はこんな感じです。






$${f(f(1))=1}$$を満たす$${\frac{1-c}{2c^3-3c^2+1}(2z^3-3z^2+1)+c}$$も、ほとんど同じような性質を持ちます。

f(f(0))=1
先程と同様に「$${c}$$について解いてから$${c}$$と$${d}$$を入れ替える」という手法により$${f(z)=\frac{1-c}{2c^3-3c^2}(2z^3-3z^2)+c}$$という関数が得られます。

凹みが2つある収束領域や$${z^4+c}$$のマンデルブロ集合に似た形が所々に見られ、この特徴は$${f(0)=1}$$である$${c(2z^3-3z^2)+1}$$と共通しています。
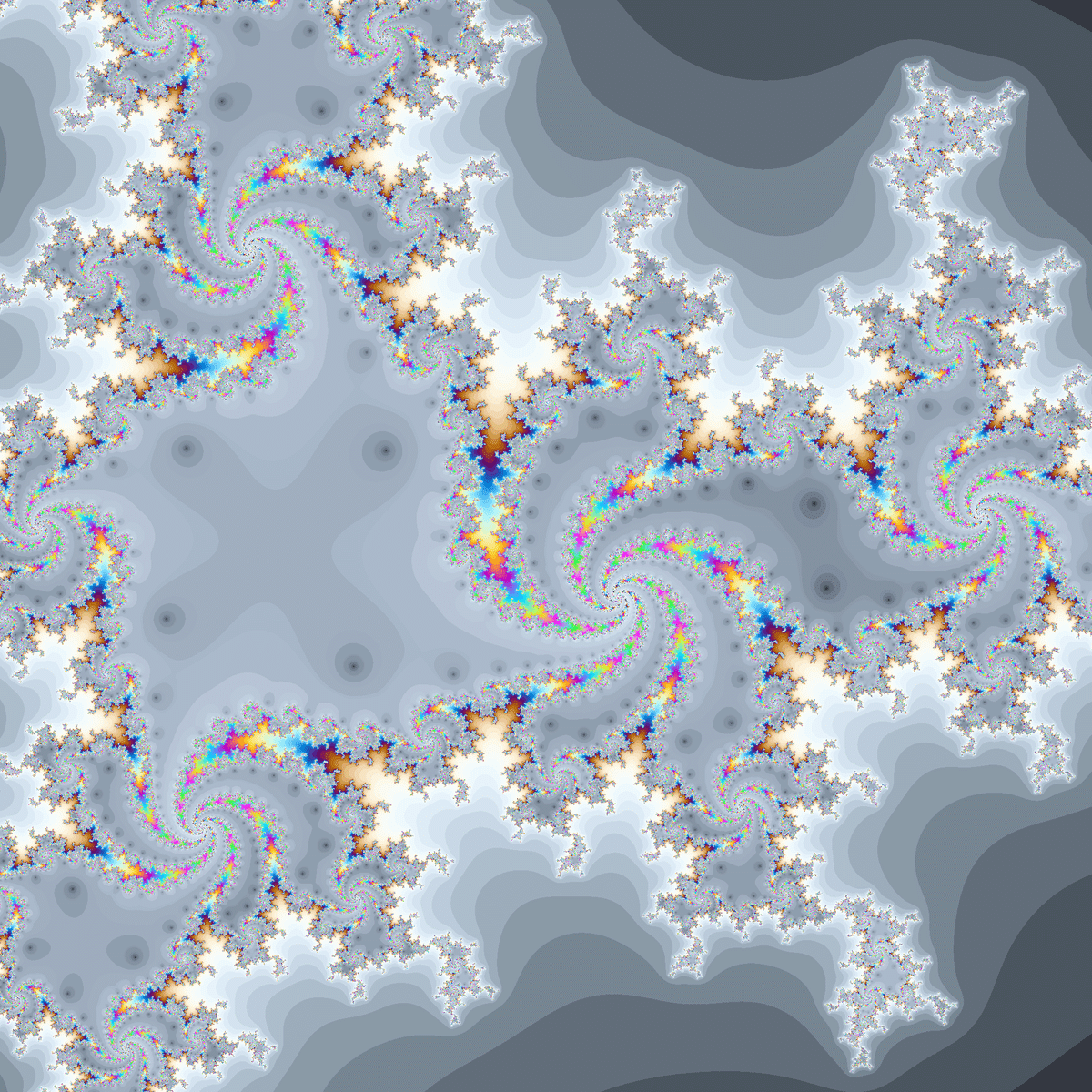


ジュリア集合に$${z^4+c}$$のような四角い領域が現れるのも$${c(2z^3-3z^2)+1}$$と一致します。
$${f(f(1))=0}$$を満たす関数は、$${-\frac{c}{2c^3-3c^2+1}(2z^3-3z^2+1)+c}$$になります。

f(f(0))=f(0)

$${f(f(0))=f(0)}$$の解には$${f(0)=0}$$の解になっているものも含まれるのですが、既に紹介したものは無視して新出の解だけを紹介していきます。




$${x=-0.5~0.5}$$、$${y=-1~1}$$という描画範囲にすると、臨界点の位置は画像の右半分の真ん中と左半分の真ん中になります。
$${c(2z^3-3z^2)+\frac{3}{2}}$$のジュリア集合では左側の臨界点(=0)は渦巻きの中心になっており、一般的にジュリア集合の渦の中心には不安定(周りにある点を吸い寄せない)な周期点があります。
$${f(f(0))=f(0)}$$かつ$${f(0)\neq0}$$を満たす場合、$${z_0=0}$$から始まる数列は$${c}$$の値に関係なく1周期のサイクルに収束しますが、$${f(0)=0}$$の場合とは異なり不安定なサイクルになるようです。

ただし例外として、$${z_0=1}$$の方の数列が1周期になるときは$${z_0=0}$$と同じ固定点に収束し、$${z_0=0}$$の固定点は吸引的になるようです。
$${f(f(1))=f(1)}$$を満たす$${c(2z^3-3z^2+1)-\frac{1}{2}}$$も同じ性質を持つようです。

f(f(0))=f(1)





$${f(0)=1}$$のものとは異なり、あまり目立った特徴は無いようです。

f(f(0))=f(f(1))


$${f(f(0))=f(f(1))}$$を愚直に計算すると$${c(2d^3-3d^2)+d=c(2(d-c)^3-3(d-c)^2)+d}$$になり、頑張って整理すると$${6d^2-(6c+6)d+2c^2+3c=0}$$という2次方程式になります。
解の公式に代入すると$${d=\frac{3c+3\pm\sqrt{-3c^2+9}}{6}}$$となりますが、複素数の平方根はいろいろと厄介な性質があって大嫌いなので平方根の消去を試みました。
根号の中身が何かしらの有理式の2乗になっていればいいので、$${-3c^2+9=e^2}$$と置きます。
この方程式は楕円の方程式なのですが、楕円や双曲線などの2変数2次方程式の有理数解は以下のように求めることができます。
まず、有理数解の具体例を1個見つけます。

今回は$${(c,e)=(0,3)}$$という解が簡単に見つけられます。
次に、傾きが有理数で先程の有理点を通る直線を考えます。
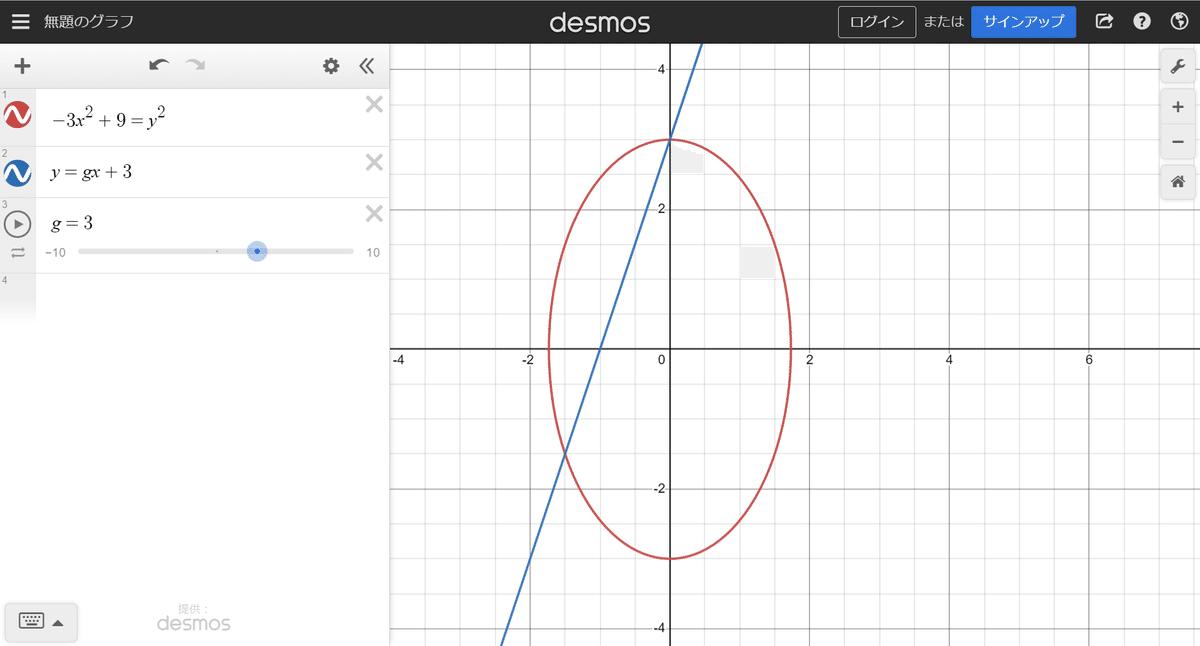
傾きを$${g}$$とすると、この直線は$${e=gc+3}$$と表せます。
この直線と楕円の交点は、以下の連立方程式を$${c}$$と$${d}$$について解くことで求められます。
$${-3c^2+9=e^2}$$
$${e=gc+3}$$
この方程式は最終的に$${e}$$か$${c}$$の2次方程式に帰着されるのですが、2次方程式の2つの解のうちの1つは$${(c,e)=(0,3)}$$に対応するものであることがすでに分かっています。
有理係数2次方程式の解のうち1つが有理数解ならばもう1つも有理数解になるので、結果として楕円と直線の交点が$${g}$$に関する有理式として得られます。
実際に解いてみると、2個目の解は$${(c,e)=(-\frac{6g}{g^2+3},\frac{18}{g^2+3}-3)}$$となり、ちゃんと$${g}$$に関する有理式になっています。
これを$${d=\frac{3c+3\pm\sqrt{-3c^2+9}}{6}}$$に代入すると、まず$${-3c^2+9=e^2}$$なので$${\frac{3c+3\pm e}{6}}$$になり、代入や整理をうまく行うことで
$${f(z)=-\frac{6g}{g^2+3}(2z^3-3z^2+\frac{1}{6}g+\frac{1}{2})+1}$$
$${f(z)=-\frac{6g}{g^2+3}(2z^3-3z^2-\frac{1}{6}g+\frac{1}{2})}$$
という関数が得られます。(先程の画像の脚注にある式は、$${g}$$を$${-c}$$に書き換えることで得られます)




計算に苦労した割に、ジュリア集合はあまり面白い形にならないようです。
また、2個目の方の解も1個目とほとんど何も変わらないようでした。

f(f(f(0)))=0
すみません、これに関しては係数が有理関数になるような解が見つかりそうにありませんでした。
実際の方程式は以下の通りです。
$${c(2(c(2d^3-3d^2)+d)^3-3(c(2d^3-3d^2)+d)^2)+d=0}$$
$${c}$$について4次、$${d}$$については9次という地獄のような方程式となってしまい、Wolfram Alphaでも因数分解できなかったので「解けない」と判断しました。

また、同様の理由により
$${f(f(f(0)))=1}$$
$${f(f(f(0)))=f(f(f(1)))}$$
も解けないと判断しました。
さらに、$${f(f(f(0)))=f(f(1))}$$はギリギリ解けそうな見た目になる($${c}$$についての2次方程式に帰着できる)のですが、平方根の消去がうまくいかなかったのでこれも解けないと判断しました。
f(f(f(0)))=f(0)


4つの収束領域が1点で接する箇所(計算精度不足によりくっついてしまっています)がありますが、そこ以外特に変わったところは無さそうです。



$${f(f(0))=0}$$の$${c(2z^3-3z^2)+\frac{3}{2}}$$と同じく、$${z_0=0}$$の固定点が不安定になるようです。
f(f(f(0)))=f(1)


飛び地が首の部分で他の領域と繋がっているあたりが、$${f(f(0))=0}$$の$${-\frac{1}{2c^2+3c}(2z^3-3z^2)+c}$$と似ている気がします。




ジュリア集合はあまり目立った特徴はありませんが、領域の繋がり方が$${-\frac{1}{2c^2+3c}(2z^3-3z^2)+c}$$のものと似ているような気がしなくもないです。
f(f(f(0)))=f(f(0))


$${f(z)=-(\frac{c}{9}+\frac{32c^3+128c}{9c^4-72c^2+144})(2z^3-3z^2)-\frac{6c-12}{c^2+12}}$$という式は、以下の手順で求めました。
$${e=c(2d^3-3d^2)}$$と置き、$${f(f(f(0)))=f(f(0))}$$を$${e}$$と$${d}$$の式で表す。
2次方程式の解の公式を使い、$${e}$$について解く。
$${f(f(0))=f(f(1))}$$の計算と同様の方法を使い、$${e}$$と$${d}$$を有理式で表す。
$${c=\frac{e}{2d^3-3d^2}}$$に代入して$${c}$$を求める。




$${f(f(0))=f(0)}$$や$${f(f(f(0)))=f(0)}$$のものと似た特徴がみられます。
これらの$${c}$$は真ん中の領域の近くにある値ですが、右側の大きな領域の周りの値だと少し違った特徴が現れます。




小さい収束領域の集合体が糸でつながったような見た目になるのですが、$${z_0=0}$$と$${z_0=1}$$の周りにある収束領域の形状やつながり方が違うように見えます。
話は変わりますが、先程説明した計算方法では$${-(\frac{c}{9}+\frac{32c^3+128c}{9c^4-72c^2+144})(2z^3-3z^2)-\frac{6c-12}{c^2+12}}$$のほかにもう1つ$${-(\frac{c^2}{72}+\frac{c}{18}+\frac{5}{18}+\frac{16c^3+64c-256}{9c^4-72c^2+144})(2z^3-3z^2)-\frac{6c-12}{c^2+12}}$$という解が出てきます。
意外なことに(?)、この関数のマンデルブロ集合は$${-(\frac{c}{9}+\frac{32c^3+128c}{9c^4-72c^2+144})(2z^3-3z^2)-\frac{6c-12}{c^2+12}}$$のものとは異なる形をしています。


しかし、ジュリア集合の方は目立った違いは見つかりませんでした。
f(z)=g^{-1}(f(g(z)))
最後に、ちょっと毛色の違うものを紹介します。

$${g(z)=1-z}$$とすると、$${f(z)=c(2z^3-3z^2+\frac{1}{2})+\frac{1}{2}}$$について$${f(z)=g^{-1}(f(g(z)))}$$が成り立ちます。
また、$${g(0)=1}$$も成り立ちます。
これにより、$${f(f(f(…f(f(f(0)))…)))}$$は以下のように変形できます。
$${f(f(f(…f(f(f(0)))…)))\\=g^{-1}(f(g(g^{-1}(f(g(g^{-1}(f(g(…g^{-1}(f(g(g^{-1}(f(g(g^{-1}(f(g(0)))))))))…)))))))))\\=g^{-1}(f(f(f(…f(f(f(g(0))))…))))\\=g^{-1}(f(f(f(…f(f(f(1)))…))))}$$
これが何を意味するかというと、$${z_0=1}$$の数列の項を$${z_n}$$とすると0が初期値の方の数列の項が$${g^{-1}(z_n)}$$と表せるので、$${z_0=0}$$の数列が収束/発散するかどうかが$${z_0=1}$$の数列の収束/発散と一致することを表しています。
要するに2つの臨界値を初期値とする2つの数列が常に同じような動きしかしないため、これも「臨界点が実質1個しかないと見做せる3次関数」の一種になります。


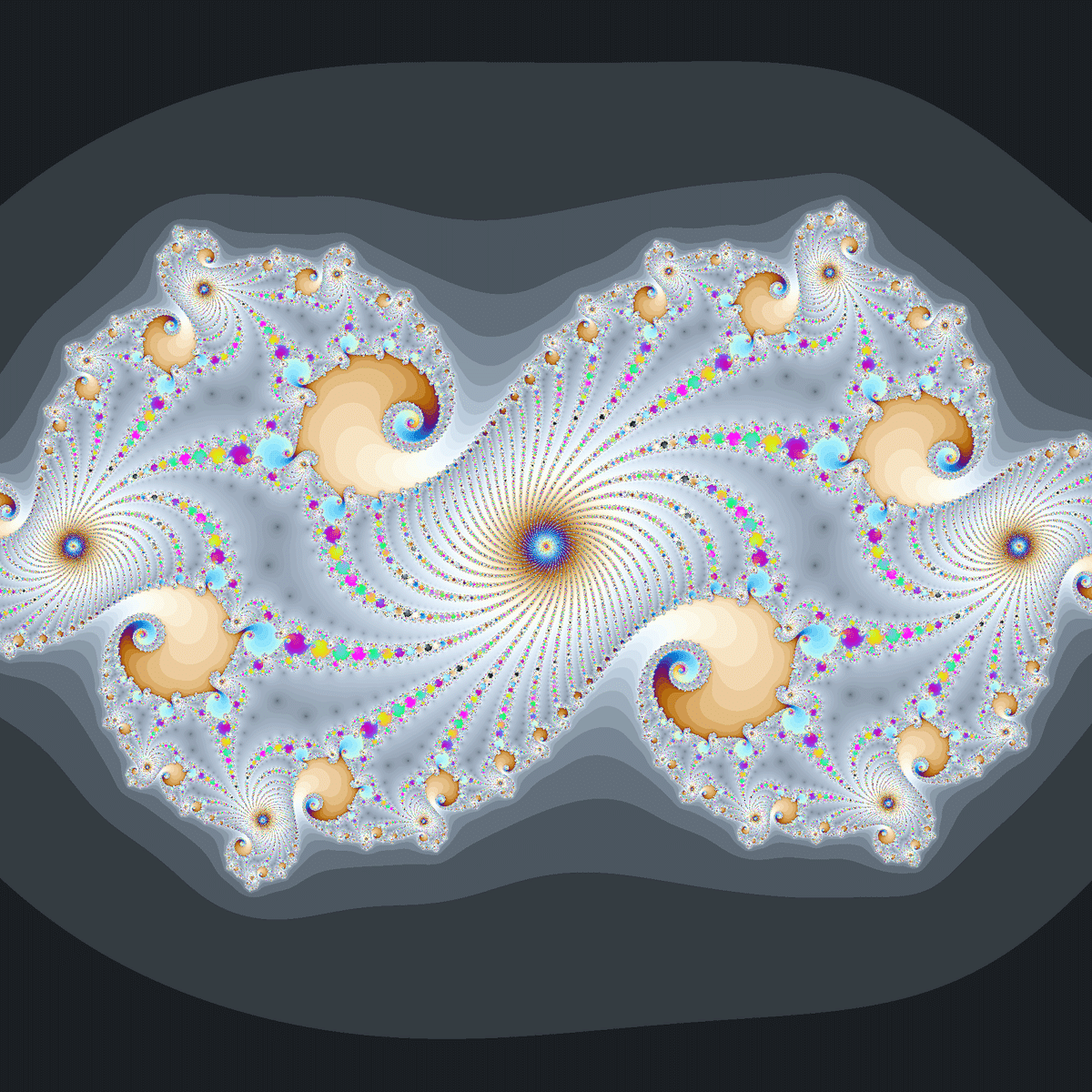
ジュリア集合は$${z_0=\frac{1}{2}}$$を中心として点対称になり、どうやら$${c(\frac{z^3}{3}-z)}$$のジュリア集合と同じような形になるようです。
※☟$${c(\frac{z^3}{3}-z)}$$のジュリア集合が載っている記事
$${f(z)=c(\frac{z^3}{3}-z)}$$の場合、$${g(z)=-z}$$とすることで$${g^{-1}(f(g(z)))}$$が成り立ちます。
こんな感じの変換によって特徴づけられる関数はもう少しバリエーションがありそうな気がするのですが、上手い計算方法が見つからなかったのでこれしか見つけられませんでした。
