今週のフラクタル35 (zB(z)+c 他)
どうも、108Hassiumです。
今回は$${zB(z)+c}$$($${B(z)=|x|+i|y|}$$、$${x}$$と$${y}$$は$${z}$$の実部と虚部)に関するフラクタル図形をお届けします。
zB(z)+c



$${zB(z)+c}$$は、以前「バーニングシップフラクタルと仲間たち3」で紹介した$${(x+iy)(|x|+i|y|)+c}$$と同じ関数です。




この関数のジュリア集合はほぼ全部「四分円に渦巻きが1個とコブみたいのがたくさんついている」という形をしていて、見た目のバリエーションがめちゃくちゃ少ないです。



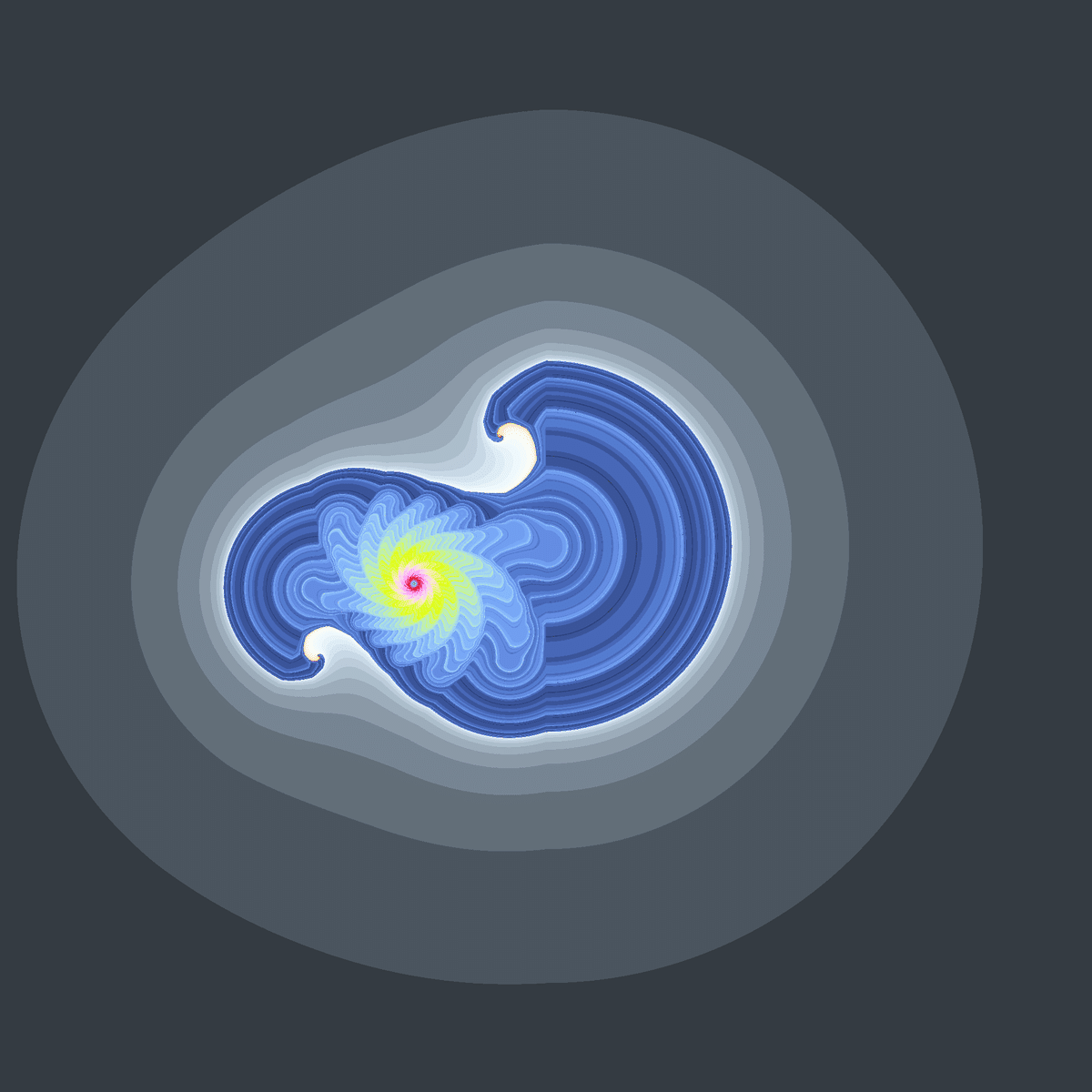
白領域のあるジュリア集合です。



$${z_0=0}$$のマンデルブロ集合の右下の部分は中途半端に切れたような形になっていましたが、やはり切れていた部分にも「収束領域のあるジュリア集合を生成する$${c}$$」が存在していたようです。





この関数は長周期なのか無限周期なのか判別困難な値が異様に多かったので、周期を算出するプログラムで10000周期以上と判定された値は無限周期の誤判定として切り捨てました。
なので、今回の高周期パラメータ探しの結果は非常に信頼性の低いものとなってしまっています。
バーニングシップフラクタルと仲間たち3
あの記事で紹介した関数のジュリア集合です。