
今週のフラクタル9 ((x+y+a,xy+b))
どうも、108Hassiumです。
今回は、以下の数列が生み出すフラクタル図形を紹介したいと思います。
$${\begin{cases}x_{n+1}=x_n+y_n+a\\y_{n+1}=x_ny_n+b\end{cases}}$$
※二変数の実数関数の組を使ったマンデルブロ集合・ジュリア集合の定義は以下の記事のものを使用します。
(x+y+a,xy+b)
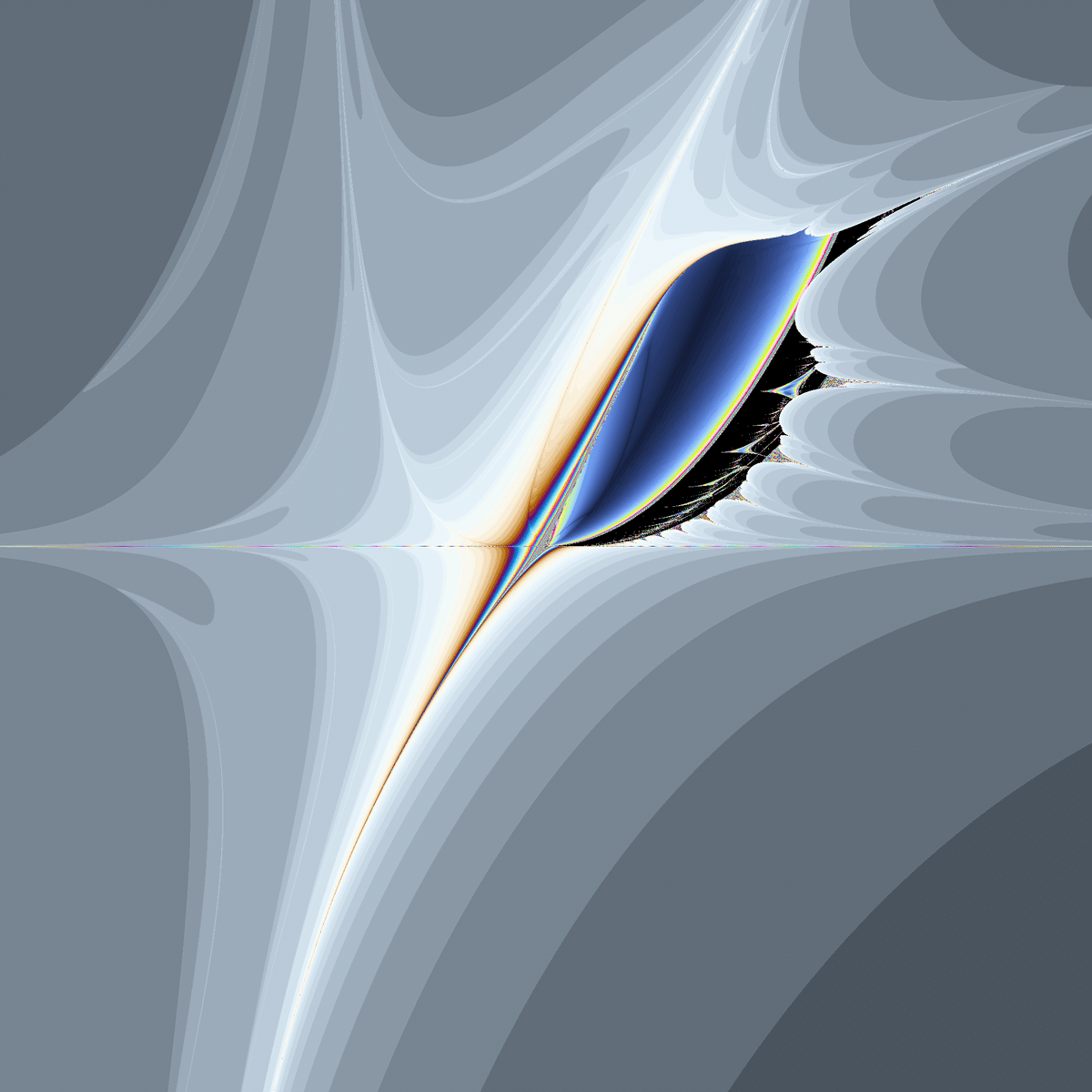



今までのような普通の複素関数(「解析的関数」というそうです)は「臨界点を初期値にすればジュリア集合の性質が反映されたマンデルブロ集合ができる」という法則がありましたが、今回のようなケース(非解析的関数)だとそのような都合のいい初期値はないようです。







ジュリア集合も、解析的関数のものとは大きく異なります。
以下の記事の画像でも見られましたが、収束領域の内部が滑らかな曲線で区切られるというのは非解析的関数ではよくある特徴らしいです。
ストレンジアトラクター
$${(x_n,y_n)}$$を座標平面にプロットしていくと、奇妙な図形が浮かび上がることがあります。

$${(a,b)=(1,-0.6)}$$のとき、$${(x_n,y_n)}$$は上の画像の白い巻貝のような領域の中を不規則に彷徨います。(暗い部分は$${(x_n,y_n)}$$が通る頻度が低く、明るい部分は高い)
このような図形を、「ストレンジアトラクター」と呼びます。
$${(x_{n+1},y_{n+1})=(x_n^2-y_n^2+a,2x_ny_n+b)}$$のような「解析的複素関数の実部と虚部」として表せるような数列ではあまり面白いストレンジアトラクターは見られませんが、そうでない関数なら今回のようなかなり単純な例でも美しいストレンジアトラクターが出現します。






