
今週のフラクタル46 (c/(con(z)^2-1)+1)
どうも、108Hassiumです。
今回は$${\frac{c}{\text{con}(z)^2-1}+1}$$($${\text{con}(z)}$$は$${z}$$の複素共役)に関するフラクタル図形をお届けします。
c/(con(z)^2-1)+1

右側は$${\frac{c}{z^2-1}+1}$$と同じような網目状の模様が見られますが、左側はよくわからない感じになっています。(真っ黒い部分は$${z_n}$$が周期数列に収束せず発散もしない領域です)
※☟$${\frac{c}{z^2-1}+1}$$に関する記事


$${\frac{c}{z^2-1}+1}$$のものとよく似た感じの、いかにも2周期発散関数っぽい見た目のジュリア集合です。


収束領域の繋がり方にcon系関数っぽい特徴が表れているジュリア集合です。



アーチ形・ハの字型接点にもう1本収束領域の集まりが繋がったY字型(?)接点が存在するジュリア集合です。

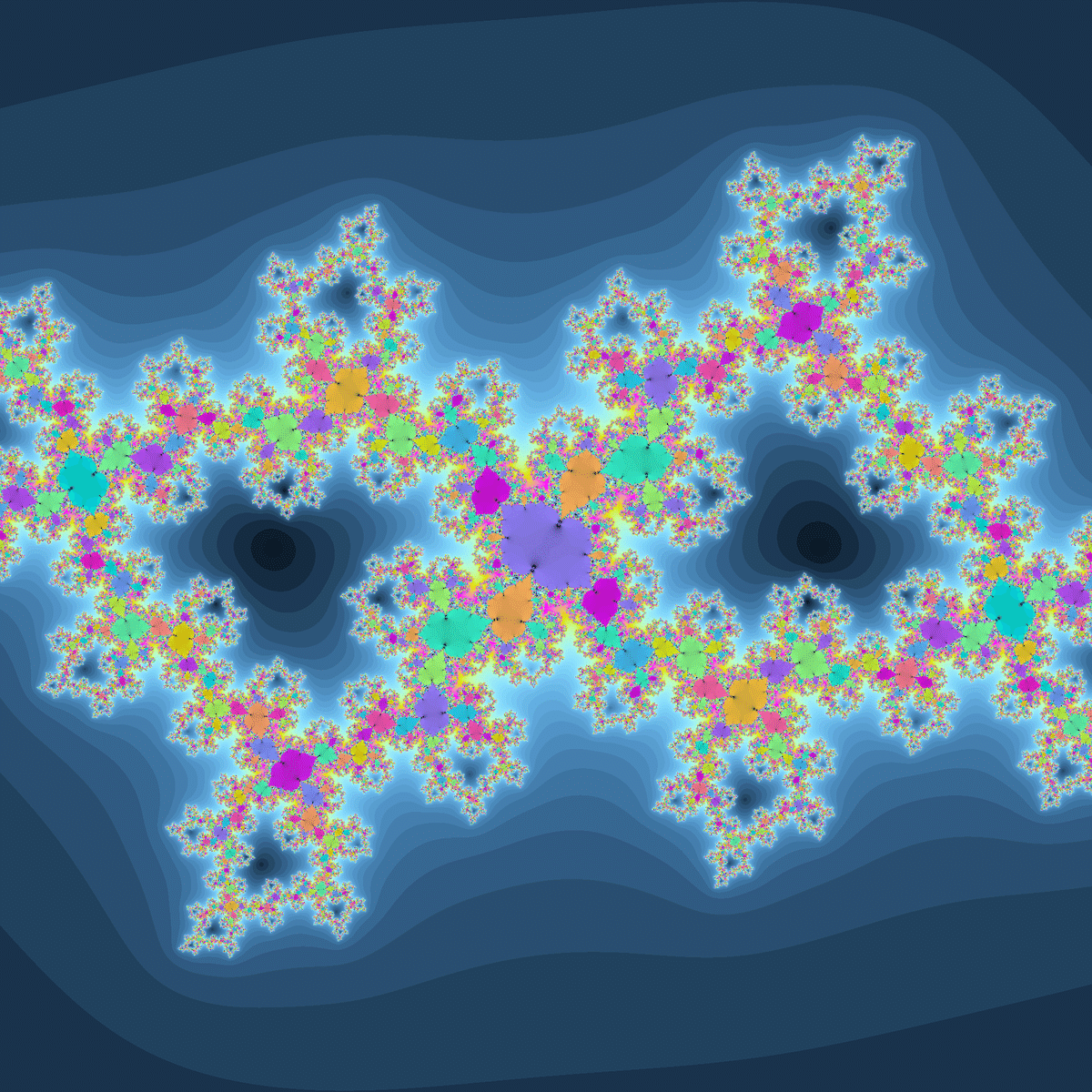


パッと見2周期発散っぽさもcon系っぽさも無い、変な形のジュリア集合です。
有限個の収束領域が環を形成するのは$${\frac{z^3}{z+0.1i}+c}$$等の摂動系の関数のジュリア集合と似ていますが、なぜ似た形になるのかは見当もつきません。





いつものです。
