どうも、108Hassiumです。
今回は$${(y+a,xy+b)}$$に関するフラクタル図形をお届けします。
(y+a,xy+b)
 ☝(y+a,xy+b)のマンデルブロ集合((x_0,y_0)=(0,0),x=-2~2,y=-2~2)
☝(y+a,xy+b)のマンデルブロ集合((x_0,y_0)=(0,0),x=-2~2,y=-2~2)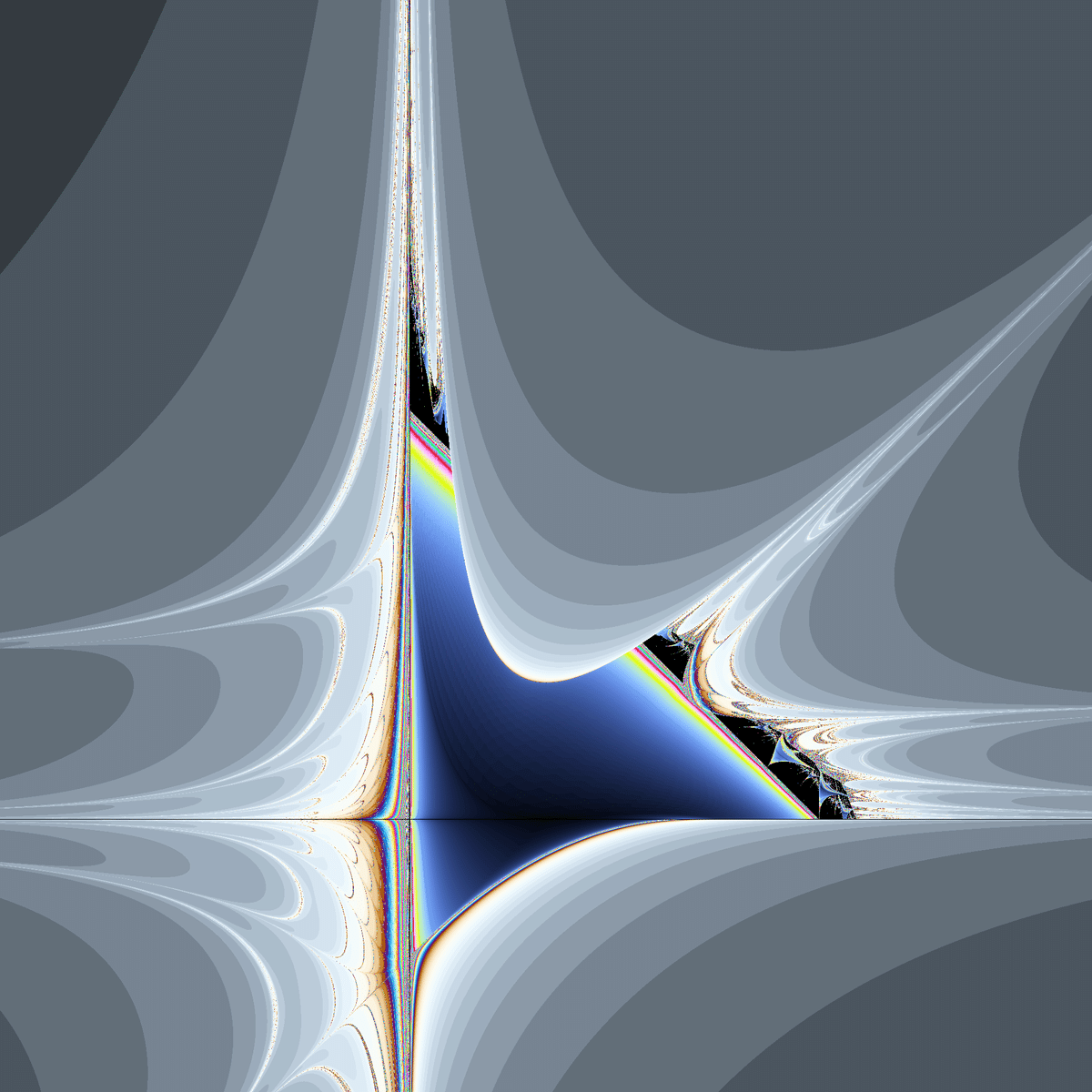 ☝(y+a,xy+b)のマンデルブロ集合((x_0,y_0)=(0,0),x=-4~4,y=-6~2)
☝(y+a,xy+b)のマンデルブロ集合((x_0,y_0)=(0,0),x=-4~4,y=-6~2)以前紹介した$${(x+y+a,xy+b)}$$や$${(y-x+a,xy+b)}$$と式の形は似ていますが、関数としては全然別物らしくマンデルブロ集合の形は大きく異なります。
※☟$${(x+y+a,xy+b)}$$の記事
※☟$${(y-x+a,xy+b)}$$の記事
 ☝(y+1.65,xy-0.7)のジュリア集合
☝(y+1.65,xy-0.7)のジュリア集合 ☝(y+1.68,xy-0.6)のジュリア集合
☝(y+1.68,xy-0.6)のジュリア集合 ☝(y-0.97,xy-0.37)のジュリア集合
☝(y-0.97,xy-0.37)のジュリア集合 ☝(y+2.13,xy-0.08)のジュリア集合
☝(y+2.13,xy-0.08)のジュリア集合 ☝(y+1.56,xy-0.96)のジュリア集合
☝(y+1.56,xy-0.96)のジュリア集合 ☝(y+1.54,xy-0.72)のジュリア集合
☝(y+1.54,xy-0.72)のジュリア集合 ☝(y+1.76,xy-0.54)のジュリア集合
☝(y+1.76,xy-0.54)のジュリア集合収束領域の端が滑らかな曲線になっていたり細く引き伸ばされたような見た目になっているという特徴は$${(x+y+a,xy+b)}$$や$${(y-x+a,xy+b)}$$と同じですが、収束領域の内部の模様は$${(x+y+a,xy+b)}$$や$${(y-x+a,xy+b)}$$と比べると少し単純に見えます。
 ☝(y+1,xy-1.27)のジュリア集合
☝(y+1,xy-1.27)のジュリア集合 ☝(y+1.99,xy-0.29)のジュリア集合
☝(y+1.99,xy-0.29)のジュリア集合白領域のあるジュリア集合です。
 ☝(y-0.78,xy-3.1)のジュリア集合
☝(y-0.78,xy-3.1)のジュリア集合 ☝(y-0.92,xy-3.49)のジュリア集合
☝(y-0.92,xy-3.49)のジュリア集合 ☝(y+0.96,xy-1.3)のジュリア集合
☝(y+0.96,xy-1.3)のジュリア集合 ☝(y+2.12,xy-0.15)のジュリア集合
☝(y+2.12,xy-0.15)のジュリア集合黒領域のあるジュリア集合です。
 ☝(y-0.8,xy-3.16)のジュリア集合(520周期)
☝(y-0.8,xy-3.16)のジュリア集合(520周期) ☝(y-0.95,xy-3.6)のジュリア集合(535周期)
☝(y-0.95,xy-3.6)のジュリア集合(535周期) ☝(y+2.09,xy-0.14)のジュリア集合(557周期)
☝(y+2.09,xy-0.14)のジュリア集合(557周期)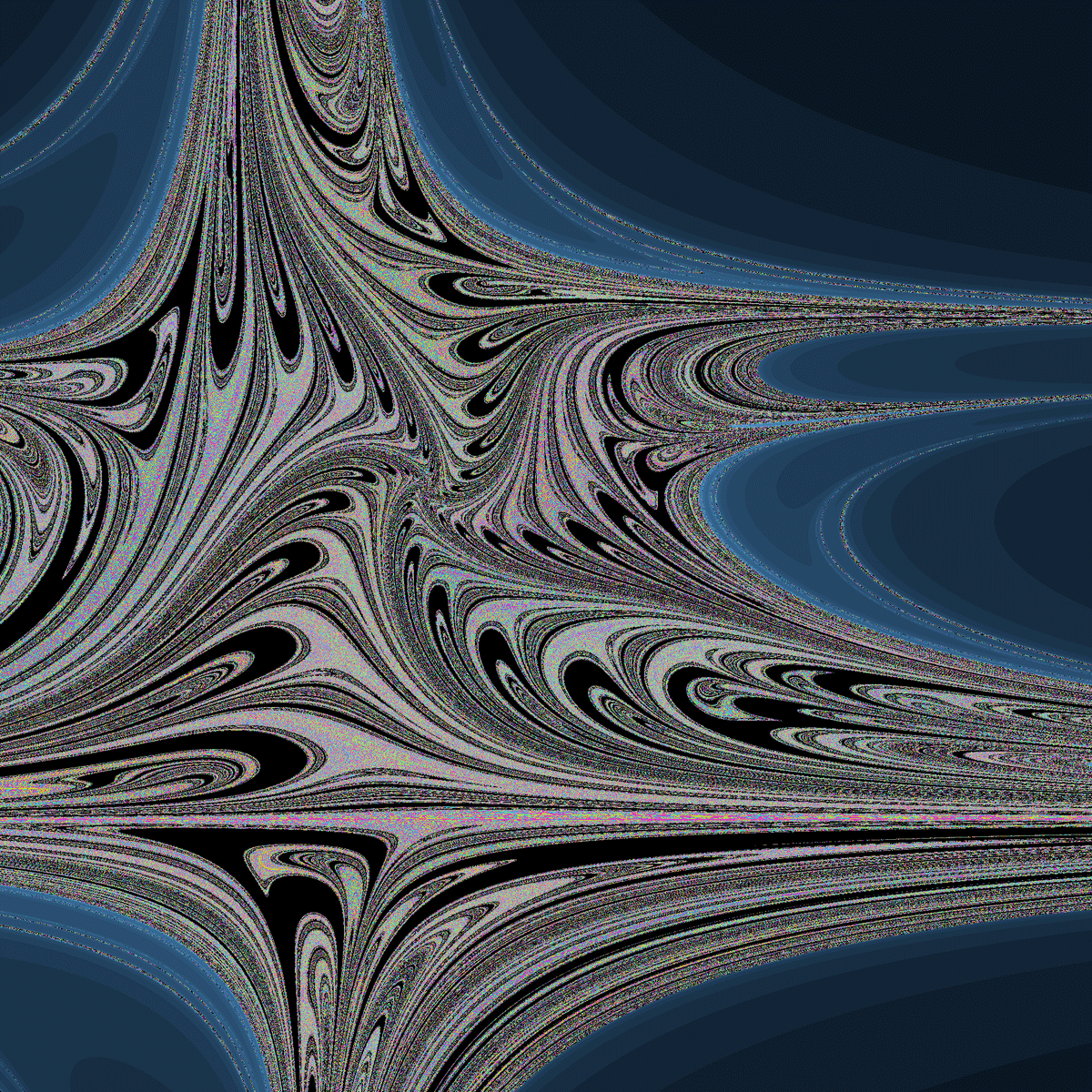 ☝(y+1.77,xy-0.53)のジュリア集合(560周期)
☝(y+1.77,xy-0.53)のジュリア集合(560周期) ☝(y-0.99,xy-3.88)のジュリア集合(738周期)
☝(y-0.99,xy-3.88)のジュリア集合(738周期)いつものです。
 ☝(y+0.94,xy-1.36)のジュリア集合とストレンジアトラクター
☝(y+0.94,xy-1.36)のジュリア集合とストレンジアトラクター ☝(y+1.74,xy-0.62)のジュリア集合とストレンジアトラクター
☝(y+1.74,xy-0.62)のジュリア集合とストレンジアトラクター ☝(y+1.94,xy-0.43)のジュリア集合とストレンジアトラクター
☝(y+1.94,xy-0.43)のジュリア集合とストレンジアトラクター
























