
今週のフラクタル2 (2z^3/(z^2+5iz+0.68)+c)
どうも、108Hassiumです。
先週から手抜き投稿用の企画を始めて見たはいいものの、加減がわからないせいで結構なボリュームの記事になってしまい、結果的に全然楽になってない気がします。
今週も結構長めになりましたが、次回あたりから画像もテキストも減っていくと思います。
2z^3/(z^2+5iz+0.68)+c

$${\frac{2z^3}{z^2+5iz+0.68}+c}$$の臨界点は0、0.2i、-10.2iの3つですが、今回は主に$${z_0=0}$$から生成されるフラクタル図形のみを扱います。



前回の$${\frac{2z^3}{z^2+4iz+0.27}+c}$$と同じように細部が崩壊していますが、こっちの方がより激しく崩れているような感じがします。
※☟前回

収束領域内に奇妙な模様のあるジュリア集合です。
陰影が付いているので立体的にも見えます。


$${z=0}$$という臨界点は2重解なので、同じく2重臨界点を持つ$${z^3+c}$$のジュリア集合と似たような三角形状の収束領域が現れることがあります。

環状に繋がった飛び地型ジュリア集合です。
周期発散関数のジュリア集合っぽい見た目ですが、$${\frac{2z^3}{z^2+5iz+0.68}+c}$$の次数は1なので周期発散関数ではありません。
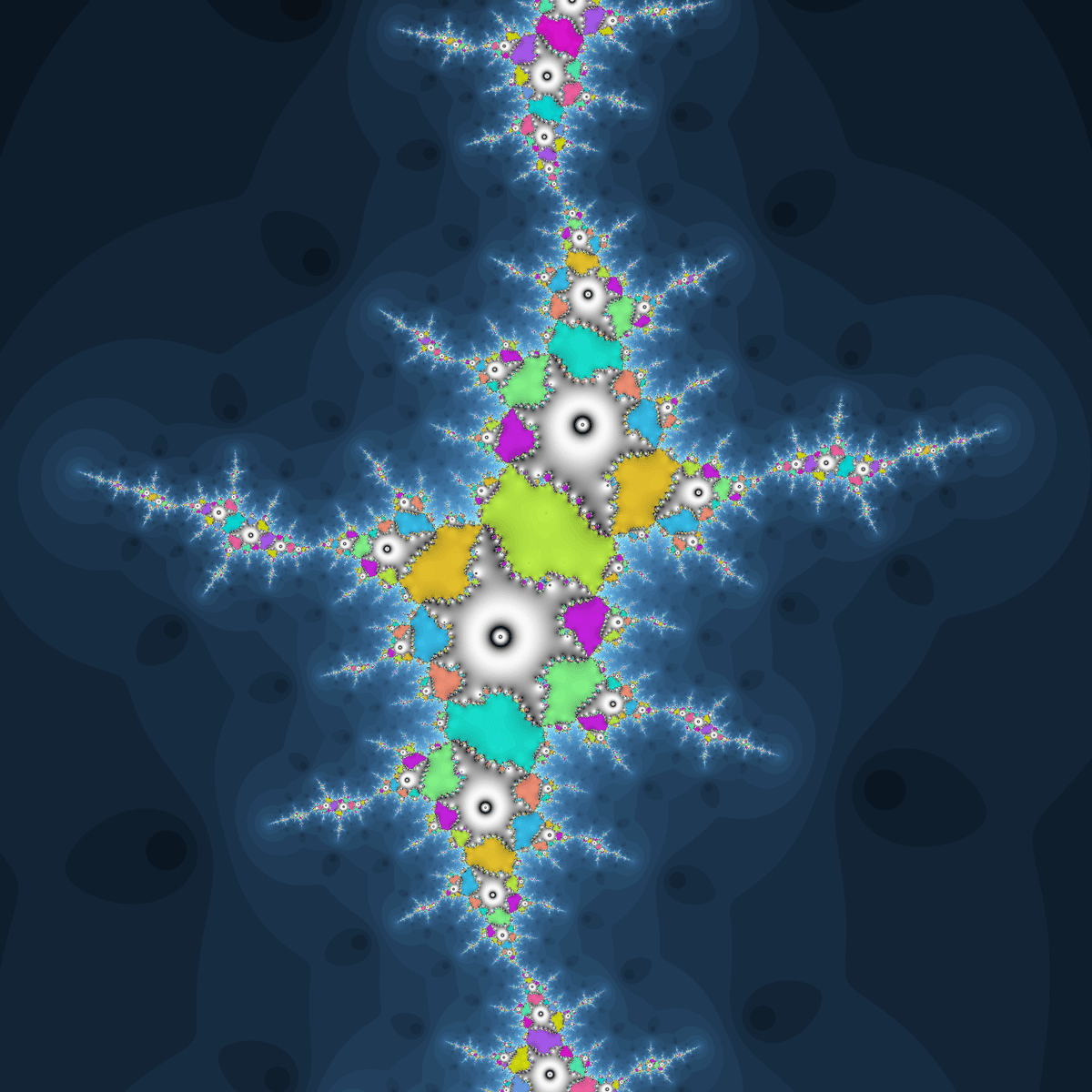

収束領域が環状に並び、その中に別サイクル($${z_0=0.2i}$$)の収束領域があるパターンのジュリア集合です。



環の内側の白い領域が花びら状に枝分かれしているパターンです。
c=1.28-0.92iの方は、なんと1440周期の480分岐です。
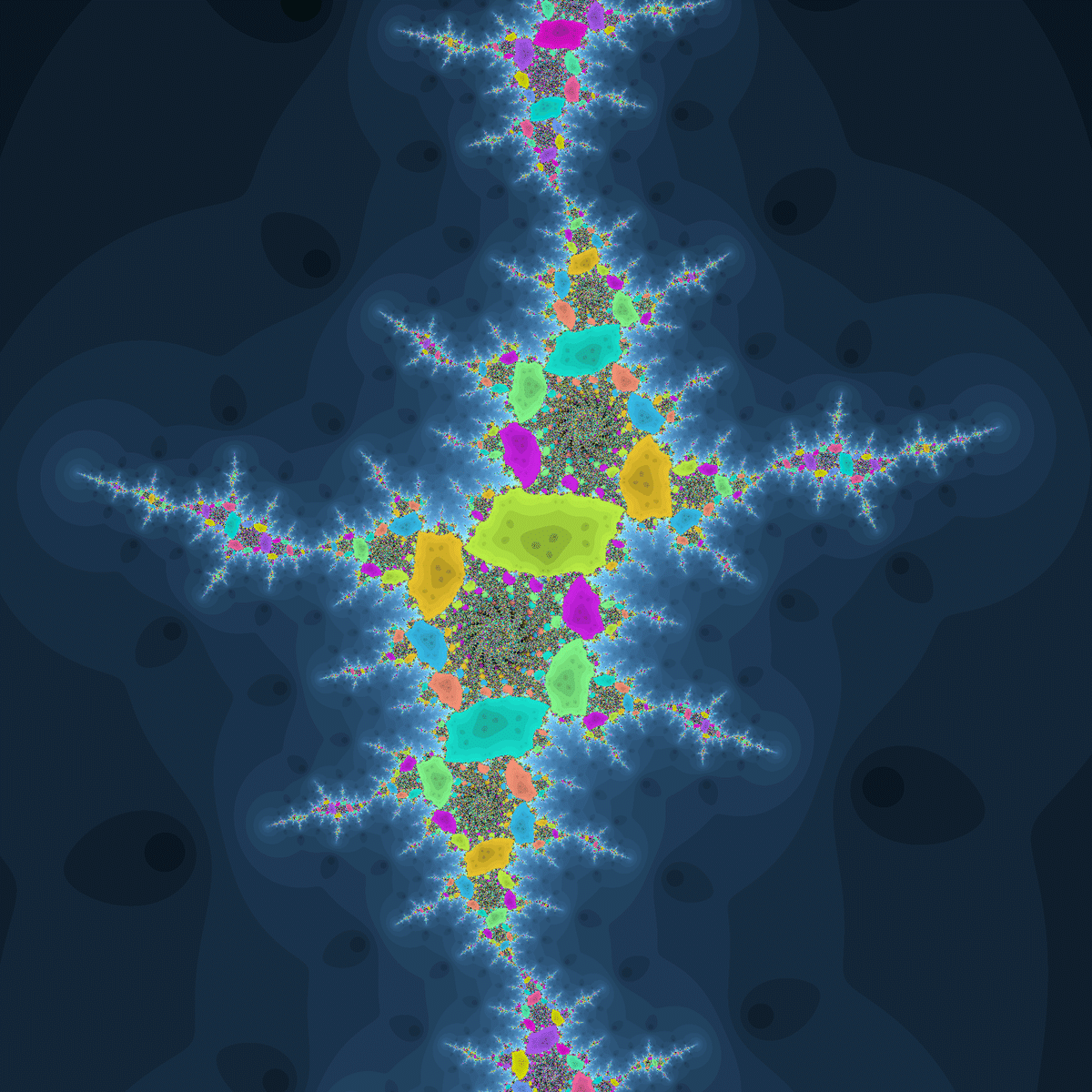


収束領域が環状に並んでいるものの、環の中に白い領域が無いパターンです。

花弁状の収束領域の周りに小さい収束領域が散らばっています。
「環の中の白領域が枝分かれするやつ」と似ていますが、花もその外側もどちらも同じサイクルの収束領域になっています。

2種類の収束領域が分岐点を共有し、なおかつ一方の領域(白い方)がもう一方の領域の中に埋まっている形のジュリア集合です。
実は前回の$${\frac{2z^3}{z^2+4iz+0.27}+c}$$でも似たようなジュリア集合が見つかっている(未掲載)のですが、第3回高周期ジュリア集合選手権のために実施した$${\frac{z^3}{z+0.1i}+c}$$の調査では1つも見つかりませんでした。
他の関数でもあまり見かけないので、個人的にこの形のジュリア集合は結構レアだと認識しています。


よくわからないけど何となくレアっぽい感じがするものです。





cの実部と虚部の小数点以下が2桁までで周期が長いものTOP5です。
1位の1.1+0.7iは小数点以下が1桁で、2桁レギュレーションで1桁が1位になるのは(未公開の記録も含めて)史上初でした。
摂動
前回の$${\frac{2z^3}{z^2+4iz+0.27}+c}$$と$${\frac{2z^3}{z^2+5iz+0.68}+c}$$は、どちらも$${\frac{2z^3}{z^2+az+b}+c}$$という形になっています。
$${a}$$と$${b}$$を実数にすると、$${y=\frac{2x^3}{x^2+ax+b}+c}$$のグラフは以下のようになります。

このグラフ、どうやら$${|a|}$$を大きくするか$${|b|}$$を小さくしていくと$${y=2x+\frac{2a^2}{x+a}-2a+c}$$のグラフと似た形になっていくようです。


ただし、似た形になるといっても$${x=0}$$の近くに特異点(極)が存在することはかわらず、関数としての性質が$${2x+\frac{2a^2}{x+a}-2a+c}$$と大きく異なるような範囲が残り続けます。
また、前回と今回で「似たような形のジュリア集合を生成する関数」として度々触れている$${\frac{z^3}{z+0.1i}+c}$$にも似たような性質があり、$${a}$$を実数とすると$${y=\frac{x^3}{x+a}+c}$$のグラフは$${|a|}$$が小さいほど$${y=x^2+c}$$に近づいていきます。

似た関数どうしは大抵似たような形のジュリア集合を生成するのですが、特異点の有無というのはジュリア集合に少なからず影響するようです。
なので$${\frac{z^3}{z+a}+c}$$のジュリア集合は、全体的なシルエットは$${z^2+c}$$のものと似ていながら穴が開いていたりバッキバキに割れたり、別サイクルの収束領域が食い込んでいたりといった感じで細部は大きく異なります。
$${\frac{2z^3}{z^2+az+b}+c}$$も同様に、$${y=2x+\frac{2a^2}{x+a}-2a+c}$$のジュリア集合を崩壊させたようなジュリア集合を生成します。($${y=2x+\frac{2a^2}{x+a}-2a+c}$$のジュリア集合は$${z^2+c}$$のものとも似た形です)
こんな感じで普通(?)のジュリア集合の関数に細工をして、ジュリア集合の細部を変形させたものを"perturbated julia set"と呼ぶらしいです。
ちなみに"perturbation"は日本語では「摂動」といい、大きな作用による運動(例えば太陽からの引力による地球の公転)が小さな作用(例えば月の引力)によって変化させられる現象を指す物理学・数学用語だそうです。
ジュリア集合とは別に、マンデルブロ集合の描画法にも摂動論を使った手法があるようです。(私は試したことないですが)
話をジュリア集合に戻します。
面白いジュリア集合を生成したい場合、摂動の影響は小さすぎても大きすぎても良くないようです。
影響が小さいと変化も小さくなりますが、大きすぎる場合も何故か普通な感じの見た目になってしまいます。

$${\frac{2x^3}{x^2+ax+b}+c}$$について、$${|b|}$$が小さいほど$${2x+\frac{2a^2}{x+a}-2a+c}$$に近くなっていく(=摂動が小さくなる)ことはすでに述べました。
$${\frac{2z^3}{z^2+4iz+0.27}+c}$$は$${\frac{2z^3}{z^2+5iz+0.68}+c}$$と比べると面白いジュリア集合が少なかったのですが、これは$${a}$$の値(4iと5i)が近いのに対して$${b}$$の値(0.27と0.68)が小さいのが原因であると考えることができます。
