
ジュリア集合の合同・相似変換
どうも、108Hassiumです。
突然ですが、皆さんはジュリア集合を縦横無尽に平行移動させたりグルングルン回転させまくったり、大きくしたりちっちゃくしたりしたいと思ったことは無いでしょうか?
この記事では、ジュリア集合を自由に平行移動・回転・縮小・拡大する方法を紹介したいと思います。
なお、この記事では「ジュリア集合」を以下のように定義します。
ジュリア集合の定義
以下の数列$${z_n}$$が無限大に発散しないような複素数$${z_0}$$全体の集合を「$${f(z)}$$のジュリア集合」と呼ぶ。
$${z_{n+1}=f(z_n)}$$
※念のため言っておくと、この定義は原義の同値な言いかえとかではなく全くの別物です。
平行移動
$${f(z+a)-a}$$($${a}$$は定数)のジュリア集合は、$${f(z)}$$のジュリア集合を平行移動したものになります。

$${f(z+a)-a}$$のジュリア集合の計算に使う数列は、以下のように変形できます。
$${z_1=f(z_0+a)-a}$$
$${z_2=f(f(z_0+a)-a+a)-a\\=f(f(z_0+a))-a}$$
$${z_3=f(f(f(z_0+a)-a+a)-a+a)-a\\=f(f(f(z_0+a)))-a}$$
$${z_4=f(f(f(f(z_0+a)-a+a)-a+a)-a+a)-a\\=f(f(f(f(z_0+a))))-a}$$
$${z_{n}=f(f(f(…f(f(f(z_0+a)-a+a)-a+a)-a…+a)-a+a)-a+a)-a\\=f(f(f(…f(f(f(z_0+a)))…)))-a}$$
関数を重ねることによって、関数の中と外にあった$${+a}$$と$${-a}$$が打ち消し合うようになり、一番内側と一番外側にだけ影響が残ります。
外側に残った$${-a}$$は数列の発散性にほとんど影響せず、せいぜい発散判定の行われるタイミングがずれて外側の模様が変わる程度です。(先程の画像でも、収束領域の周りの模様が変わっています)
そして内側の$${+a}$$は、初期値をずらす効果があります。
$${(z+i)^2+0.3+0.5i-i}$$のジュリア集合の計算では$${z_0=1}$$とすると$${z^2+0.3+0.5i}$$のジュリア集合における$${z_0=1+i}$$のときの数列が計算され、$${z^2+0.3+0.5i}$$のジュリア集合での$${z_0=0}$$の計算は$${z_0=-i}$$のときの計算に対応しています。
このような仕組みにより、$${f(z+a)-a}$$のジュリア集合は$${f(z)}$$のジュリア集合を$${-a}$$平行移動したものになります。
※先程の画像は諸事情により上下逆に描画されているので、$${a=i}$$とすることにより上方向に移動しています。

回転・縮小・拡大
$${\frac{1}{a}f(az)}$$のジュリア集合は、$${f(z)}$$のジュリア集合を回転・縮小・拡大したものになります。
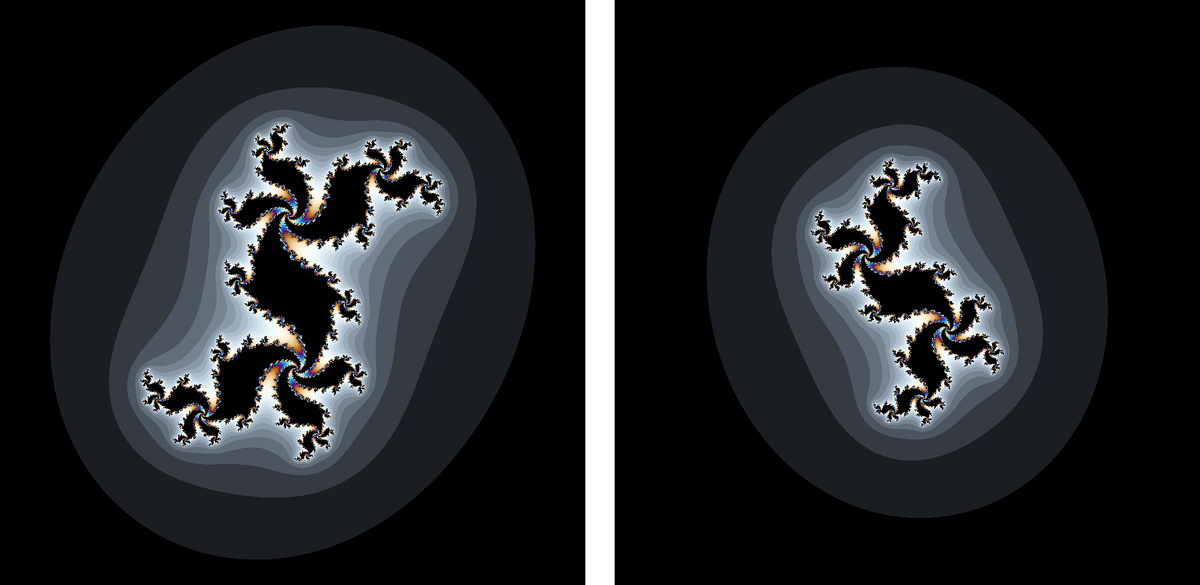
$${\frac{1}{a}f(az)}$$のジュリア集合の計算に使う数列は、以下のように変形できます。
$${z_1=\frac{1}{a}f(az_0)}$$
$${z_2=\frac{1}{a}f(a×\frac{1}{a}f(az_0))\\=\frac{1}{a}f(f(az_0))}$$
$${z_3=\frac{1}{a}f(a×\frac{1}{a}f(a×\frac{1}{a}f(az_0)))\\=\frac{1}{a}f(f(f(az_0)))}$$
$${z_4=\frac{1}{a}f(a×\frac{1}{a}f(a×\frac{1}{a}f(a×\frac{1}{a}f(az_0))))\\=\frac{1}{a}f(f(f(f(az_0))))}$$
$${z_n=\frac{1}{a}f(a×\frac{1}{a}f(a×\frac{1}{a}f(a×…\frac{1}{a}f(a×\frac{1}{a}f(a×\frac{1}{a}f(az_0)))…)))\\=\frac{1}{a}f(f(f(…f(f(f(az_0)))…)))}$$
関数を重ねることによって、関数の中と外にあった$${a}$$と$${\frac{1}{a}}$$が打ち消し合うようになり、一番内側と一番外側にだけ影響が残ります。
外側に残った$${\frac{1}{a}}$$は数列の発散性にほとんど影響せず、せいぜい発散判定の行われるタイミングがずれて外側の模様が変わる程度です。
そして内側の$${a}$$は、初期値をずらす効果があります。
$${\frac{1}{1+i}((1+i)z)^2+0.3+0.5i}$$のジュリア集合の計算では$${z_0=1}$$とすると$${z^2+0.3+0.5i}$$のジュリア集合における$${z_0=1+i}$$のときの数列が計算され、$${z^2+0.3+0.5i}$$のジュリア集合での$${z_0=1}$$の計算は$${z_0=\frac{1}{1+i}}$$のときの計算に対応しています。
このような仕組みにより、$${\frac{1}{a}f(az)}$$のジュリア集合は$${f(z)}$$のジュリア集合に対して以下のような関係を持ちます。
$${|a|=1}$$:$${-\text{arg}(a)}$$回転
$${|a|>1}$$かつ$${\text{arg}(a)=0}$$:$${\frac{1}{a}}$$倍縮小
$${|a|<1}$$かつ$${\text{arg}(a)=0}$$:$${\frac{1}{a}}$$倍拡大
その他:上記の組み合わせ

まとめ
以上の結果を踏まえると、ある1次関数$${g(z)=az+b}$$を用いて$${g^{-1}(f(g(z)))}$$と表せる関数のジュリア集合が$${f(z)}$$のジュリア集合に回転・縮小・拡大・平行移動を施したものになることがわかります。

また、ほぼ同じような考え方により$${\text{con}(f(\text{con}(z)))}$$($${\text{con}(z)}$$は$${z}$$の複素共役)が鏡映変換に対応していることも分かります。
応用
せっかくなので、1次関数による合同・相似変換の概念の応用例を紹介します。
2次関数の自由度
2次関数といえば$${ax^2+bx+c}$$という3自由度の一般式を高校で習いますが、実はジュリア集合の合同・相似変換で移り合うものを同一視すると自由度は1変数分しかなくなります。
実際、$${f(z)=az^2+bz+c}$$、$${g(z)=\frac{1}{a}z-\frac{b}{2a}}$$とすると、$${g^{-1}(f(g(z)))}$$は以下のようになります。
$${g^{-1}(f(g(z)))=a(a(\frac{1}{a}z-\frac{b}{2a})^2+b(\frac{1}{a}z-\frac{b}{2a})+c+\frac{b}{2a})}$$
$${=a(a(\frac{1}{a^2}z^2-\frac{b}{a^2}z+\frac{b^2}{4a^2})+\frac{b}{a}z-\frac{b^2}{2a}+c+\frac{b}{2a})}$$
$${=z^2-bz+\frac{b^2}{4}+bz-\frac{b^2}{2}+ac+\frac{b}{2}}$$
$${=z^2+ac-\frac{b^2}{4}+\frac{b}{2}}$$
$${ac-\frac{b^2}{4}+\frac{b}{2}=C}$$と書き換えることで、$${z^2+C}$$という見慣れた形の式に変形できます。
これは「$${az^2+bz+c}$$のジュリア集合は、$${z^2+C}$$のジュリア集合に回転・縮小・拡大・平行移動を施したものしかない」という事を意味するのですが、実は意外な副産物があります。
以下の記事で、「$${c}$$が$${z^2+c}$$のマンデルブロ集合のフチの位置にあるとき、特殊なジュリア集合が生成される」という話をしました。


ハート形の部分は「カージオイド」という図形で、曲線上からキリのいい座標の点を見つけるのは難しそうです。
一方、$${c(z^2-z)}$$のマンデルブロ集合はこんな形をしています。

真ん中の丸い領域は、どうやら半径1の円になっているようです。
単位円周上の有理点を探すのは簡単なので、$${c(z^2-z)}$$のジュリア集合から$${z^2+c}$$のジュリア集合への相似変換ができれば$${z^2+c}$$の周上のキリのいい値の点を見つけることができそうです。
先程の相似変換の式を使って$${c(z^2-z)}$$を$${z^2+C}$$の形に変形すると、$${C=-\frac{c^2}{4}+\frac{c}{2}}$$となります。
実際に単位円周上の$${c}$$の値を代入してみると$${C}$$はカージオイド上の点になるようで、0.6+0.8iなどの値を代入することで目的の値を得ることができます。

3次関数の自由度
2次関数と同様に、3次関数の(ジュリア集合の形状についての)自由度についても4より少ないことを確認できます。
3次関数$${f(z)}$$を$${az^3+bz^2+cz+d}$$と置き、この関数の係数を1次関数$${g(z)=ez+h}$$を使って減らすことを考えます。
まず、$${g^{-1}(f(g(z)))}$$を展開します。
$${g^{-1}(f(g(z)))}$$
$${=\frac{1}{e}(a(ez+h)^3+b(ez+h)^2+c(ez+h)+d-h)}$$
$${=\frac{1}{e}(a(e^3z^3+3e^2hz^2+3eh^2z+h^3)+b(e^2z^2+2ehz+h^2)^2+c(ez+h)+d-h)}$$
$${=\frac{1}{e}(ae^3z^3+(3ae^2h+be^2)z^2+(3aeh^2+2beh+ce)z+ah^3+bh^2+ch+d-h)}$$
$${=ae^2z^3+(3aeh+be)z^2+(3ah^2+2bh+c)z+\frac{1}{e}(ah^3+bh^2+ch+d-h)}$$
ここから$${e}$$と$${h}$$を使って係数を消していくとなると、3次と2次の係数を消すのが簡単そうです。
というわけで、以下の連立方程式を解いてみます。
$${ae^2=1}$$
$${3aeh+be=0}$$
これを$${e}$$と$${h}$$について解くと以下のような解が得られます。
$${e=\frac{1}{\sqrt{a}}}$$
$${h=-\frac{b}{3a}}$$
これを$${g^{-1}(f(g(z)))}$$の式に代入すると以下のようになります。
$${g^{-1}(f(g(z)))=z^3+(-\frac{b^2}{3a}+c)z+\sqrt{a}(\frac{2b^3}{27a^2}+\frac{b-bc}{3a}+d)}$$
$${C=-\frac{b^2}{3a}+c}$$、$${D=\sqrt{a}(\frac{2b^3}{27a^2}+\frac{b-bc}{3a}+d)}$$と置くことで、$${az^3+bz^2+cz+d}$$のジュリア集合は$${z^3+Cz+D}$$のジュリア集合を平行移動・回転・縮小・拡大したものであることがわかります。
なお、マンデルブロ集合を描画するために臨界点を計算することを考えると$${z^3+Cz+D}$$よりも$${z^3+Cz^2+D}$$や$${C(\frac{z^3}{3}-\frac{z^2}{2})+D}$$という形の式の方が便利なのですが、これらの式は連立方程式の立て方を変えたり$${z^3+Cz+D}$$にさらに変換をかけたりすることで導出できます。
また、一般の$${n}$$次多項式関数においても、1次関数の係数が2つあるので係数を2つ消すことができ、自由度は$${n-1}$$個になることが予想できます。(係数の消し方によっては5次以上の高次方程式が出てくる可能性もありますが、解が存在することさえわかれば特定の式が標準形として使えることを確認するには十分です)
一般の多項式関数に関する話が出てきたので、ついでに他の話をします。
2次関数の自由度の話に出てきた記事では、「$${z^5+c}$$と$${(-c)^{\frac{4}{5}}(z^5-1)}$$のジュリア集合は相似」という話もしていました。
※☟再掲
実はこの性質も、1次関数による合同・相似変換で説明できます。
$${f(z)=z^5+c}$$、$${g(z)=az}$$とすると、
$${g^{-1}(f(g(z)))=a^4z^5+\frac{c}{a}=a^4(z^5+\frac{c}{a^5})}$$
となり、$${a=(-c)^{\frac{1}{5}}}$$とすることで$${z^5+c}$$と$${(-c)^{\frac{4}{5}}(z^5-1)}$$のジュリア集合が相似相似であることがわかります。
