今週のフラクタル63　((0.5+0.9i)(z^3+1)/(x^2+y^2-2)+c)

どうも、108Hassiumです。

今回は$${\frac{(0.5+0.9i)(z^3+1)}{x^2+y^2-2}+c}$$($${x}$$と$${y}$$は$${z}$$の実部と虚部)に関するフラクタル図形をお届けします。

(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+c

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+cのマンデルブロ集合(a=-2~2,b=-2~2)

マンデルブロ集合を囲んでいる黒い帯状の模様は、おそらく分母=0の解が円上に分布していることに由来すると思われます。(要は$${x^2+y^2-2=0}$$をトラップにしたorbit trapと同じです)

なおマンデルブロ集合の形状が線対称っぽいのも特徴的ですが、これの理由は不明です。(そもそも本当に線対称かどうかも不明です)

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+cのマンデルブロ集合(a=0~4,b=0~4)

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+cのマンデルブロ集合(a=0~40,b=0~40)

原点から少し離れた位置に、めちゃくちゃ長い収束領域があります。

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+cのマンデルブロ集合(1.3+2.2i付近の20倍拡大)

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+cのマンデルブロ集合(0.5396+1.1325i付近の20000倍拡大)

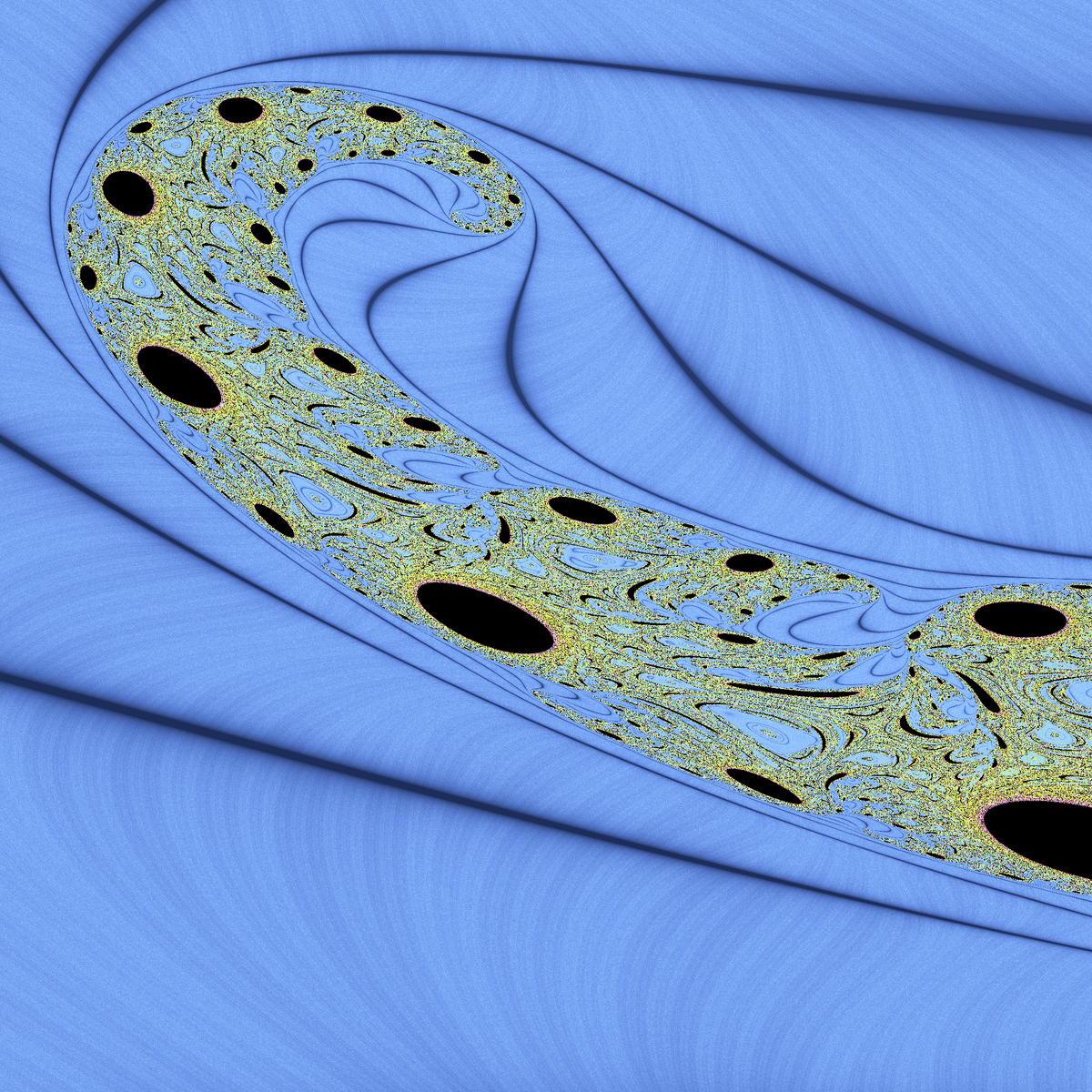
拡大図です。

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+0.32-0.23iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+1.05+0.61iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+1.13+0.04iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+0.86+0.96iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)-0.55+1.03iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+0.89+0.9iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+0.68-0.31iのジュリア集合

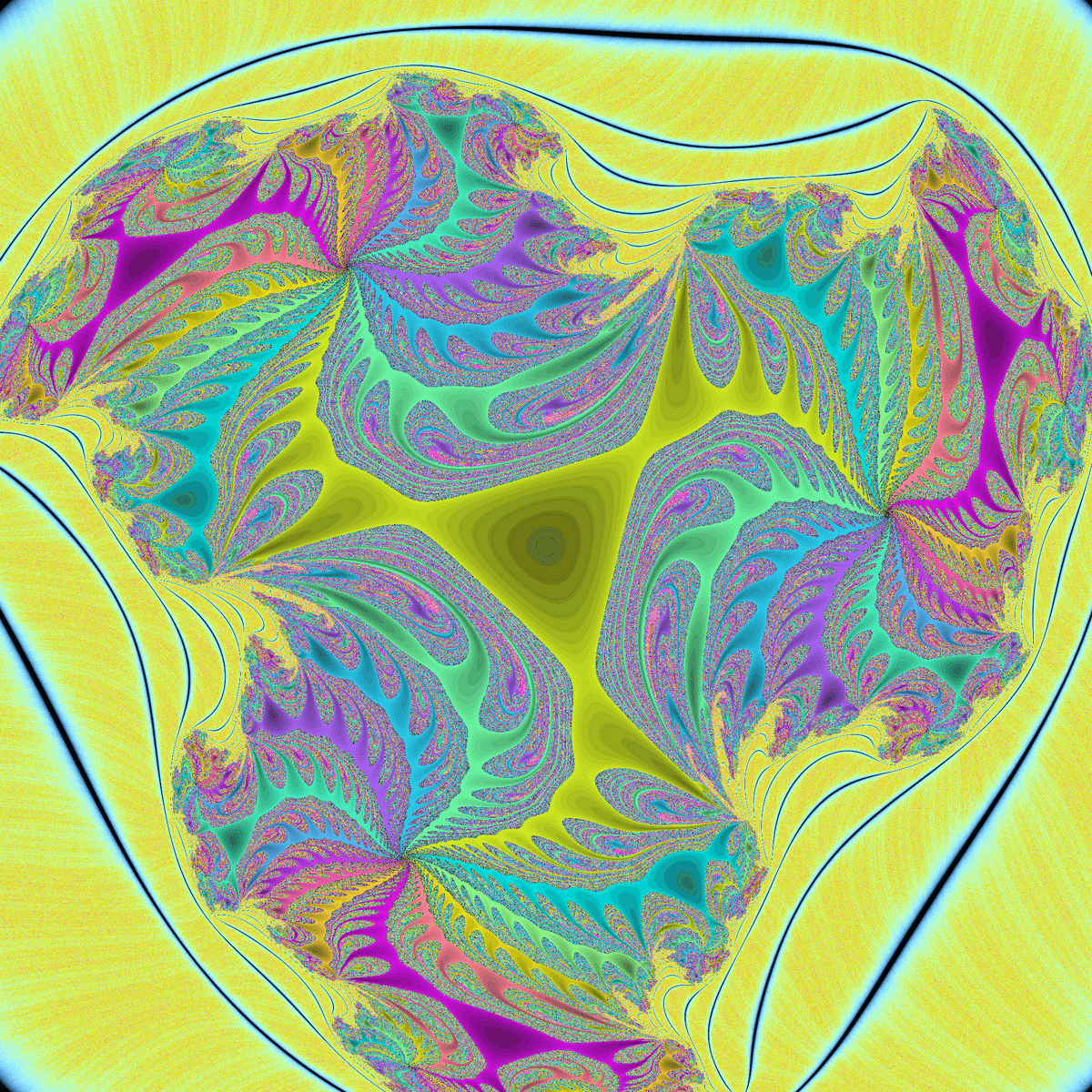
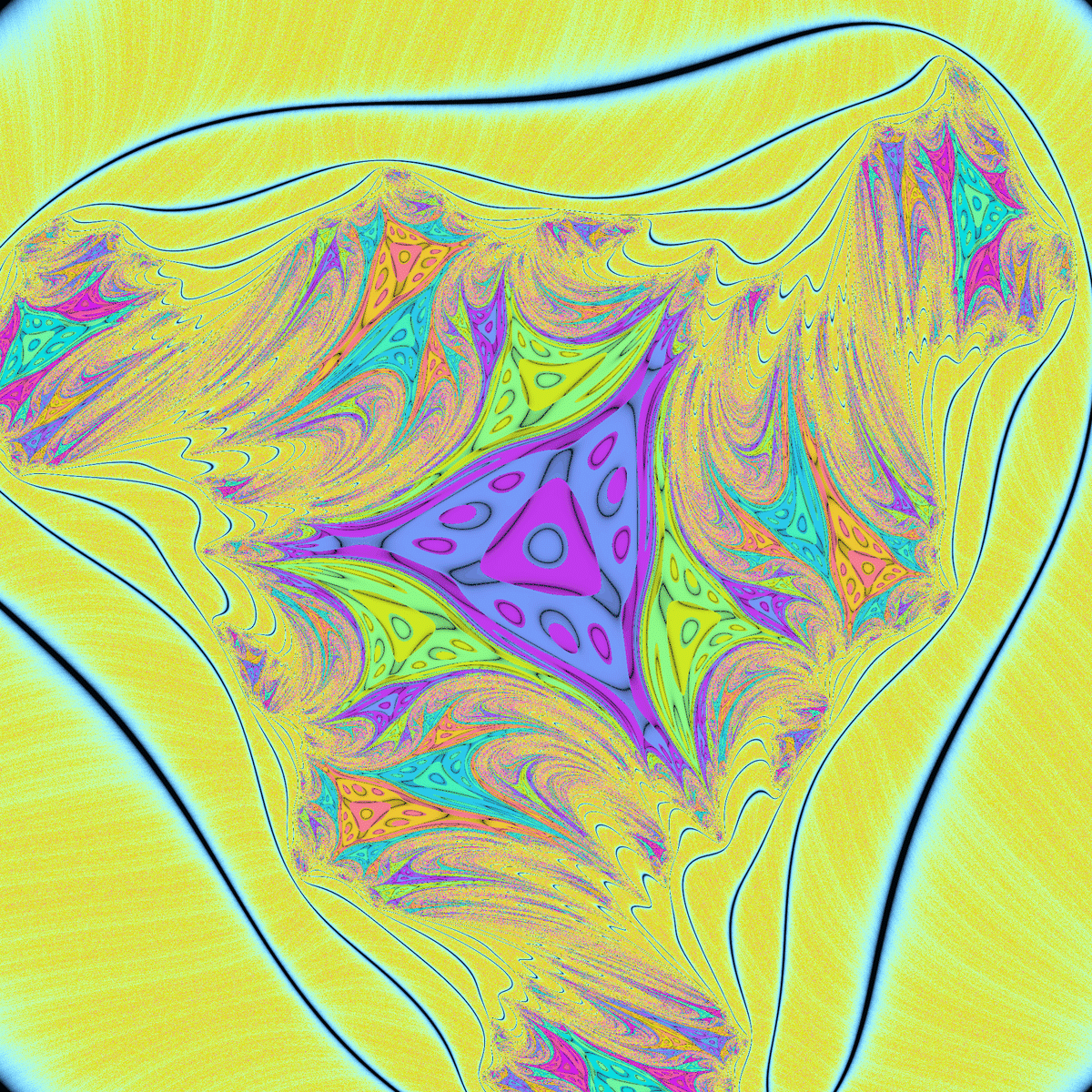
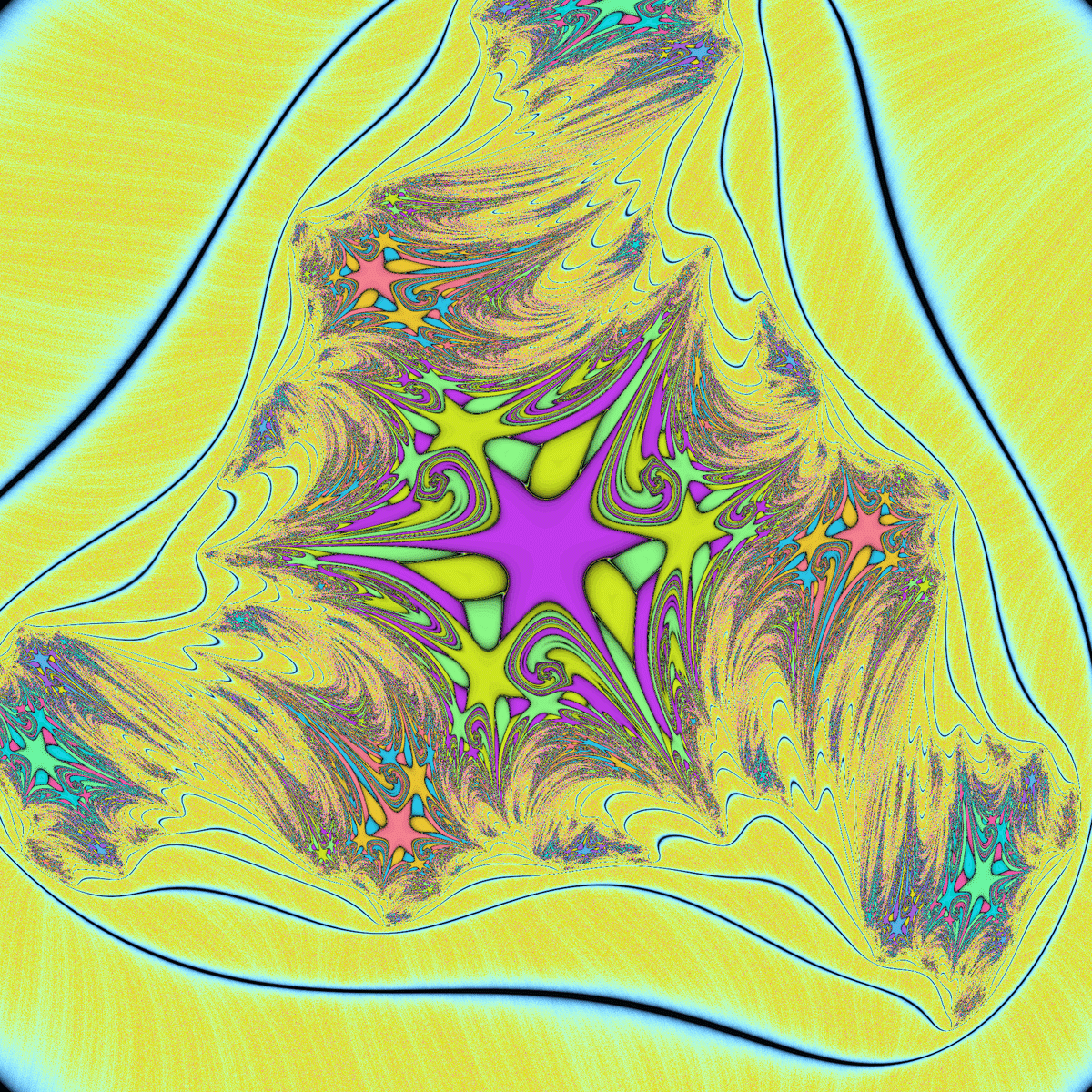
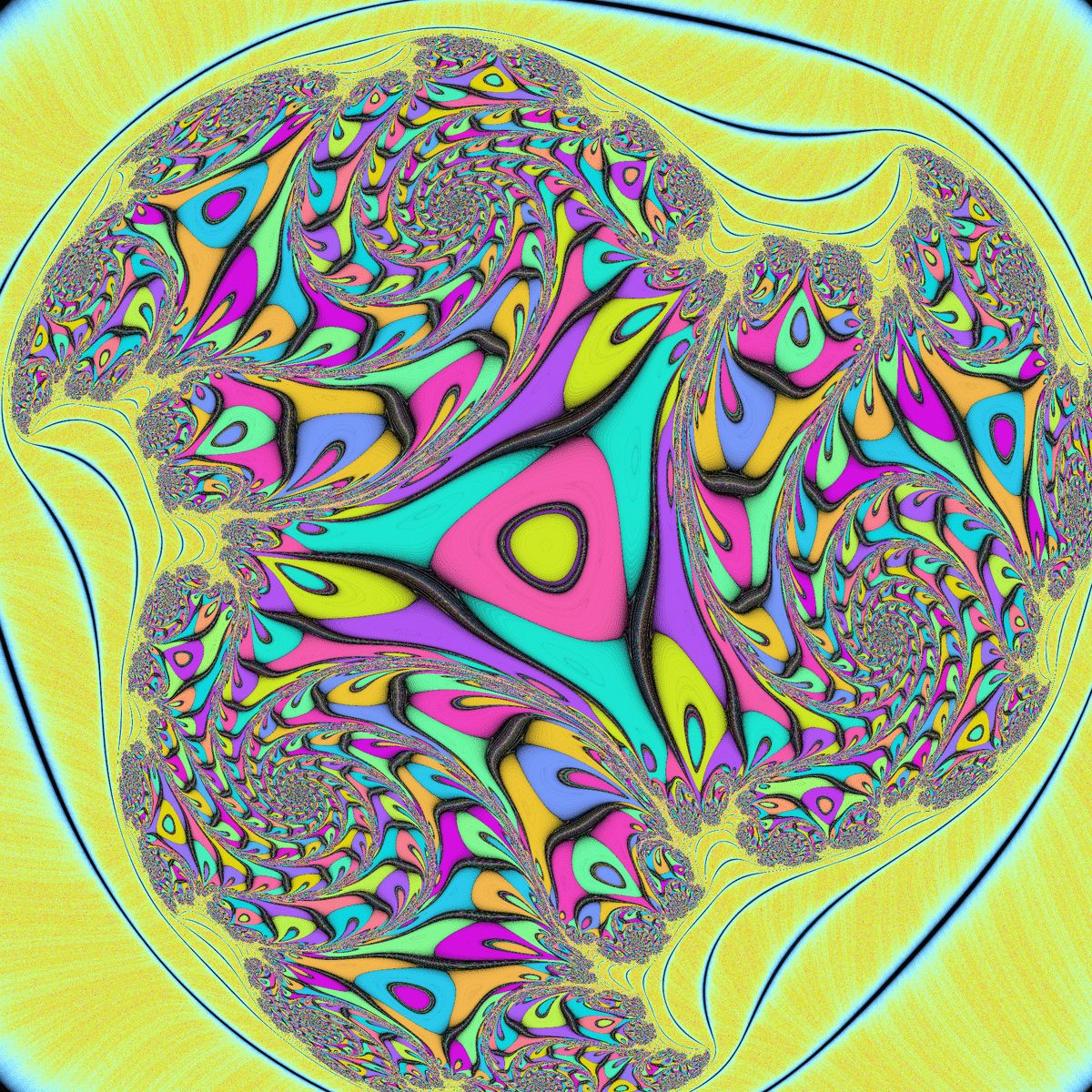
ジュリア集合は、マンデルブロ集合と同様の環状の模様があるのに加えて3回回転対称である点が特徴的です。

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+1.04+0.19iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)-0.49+0.28iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)-0.43+0.23iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+0.54+1.13iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+1.08+0.06iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)+0.37+1.23iのジュリア集合

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)-0.03+1.22iのジュリア集合

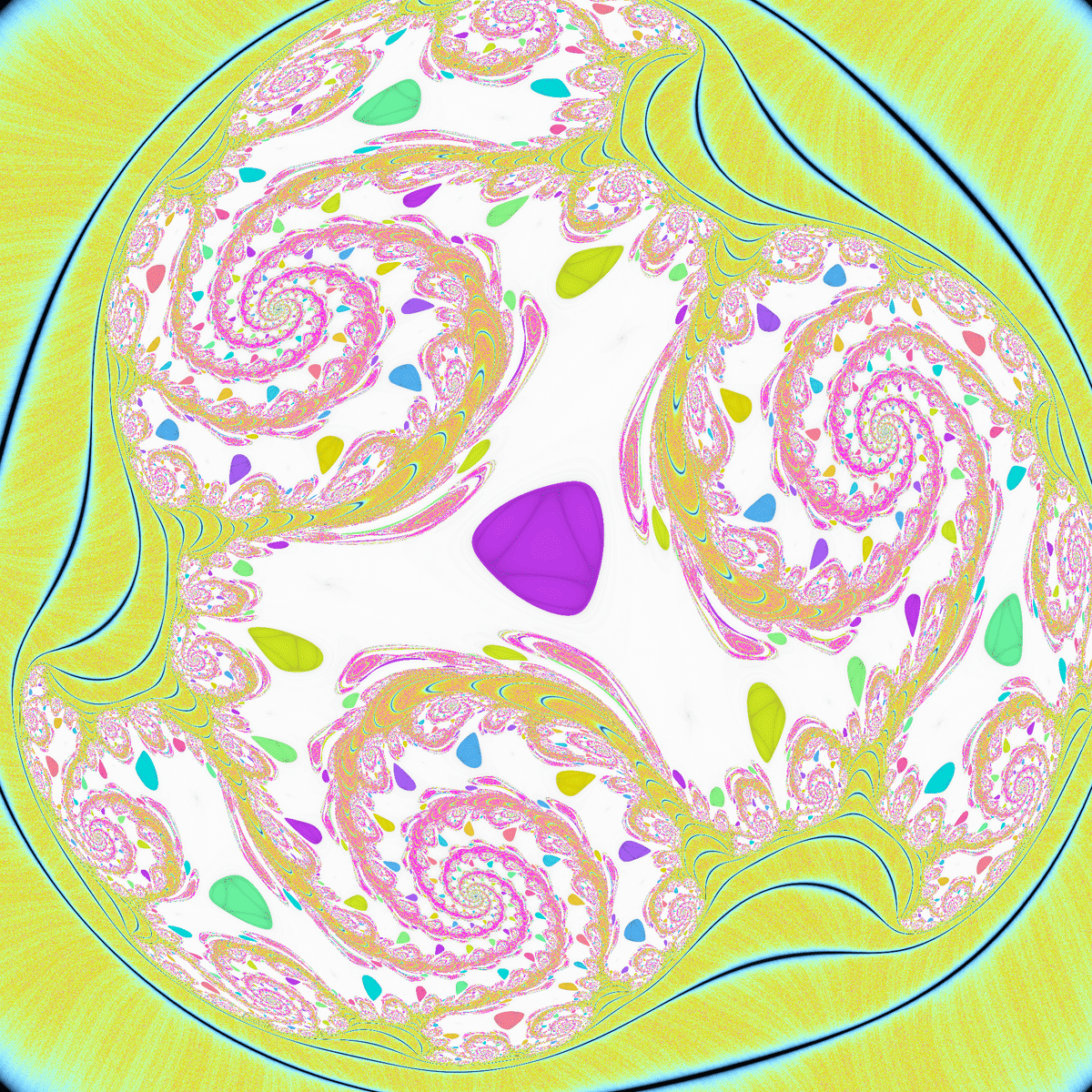
2種類の吸引的サイクルが存在するジュリア集合です。

☝(0.5+0.9i)(z^3+1)/(x^2+y^2-2)-0.37+1.02iのジュリア集合

3種類の吸引的サイクルが存在するジュリア集合です。