
今週のフラクタル29 ((0.9+0.5i)(z+z/(3z^2-1))+c)
どうも、108Hassiumです。
今回は$${(0.9+0.5i)(z+\frac{z}{3z^2-1})+c}$$に関するフラクタル図形をお届けします。
(0.9+0.5i)(z+z/(3z^2-1))+c

$${(0.9+0.5i)(z+\frac{z}{3z^2-1})+c}$$は次数が1の有理関数かつ1次の項の係数が$${0.9+0.5i}$$なので、同じ特徴を持つ$${(0.9+0.5i)(z+\frac{1}{z})+c}$$といろいろなところが似ています。
※☟$${(0.9+0.5i)(z+\frac{1}{z})+c}$$の記事



$${(0.9+0.5i)(z+\frac{z}{3z^2-1})+c}$$の臨界点は±1と0で、$${z_0=±1}$$のマンデルブロ集合の形は同じですが$${z_0=0}$$のものはそれらとは違う形になります。
z_0=1
ジュリア集合です。







$${(0.9+0.5i)(z+\frac{1}{z})+c}$$のものと似たような見た目のジュリア集合です。
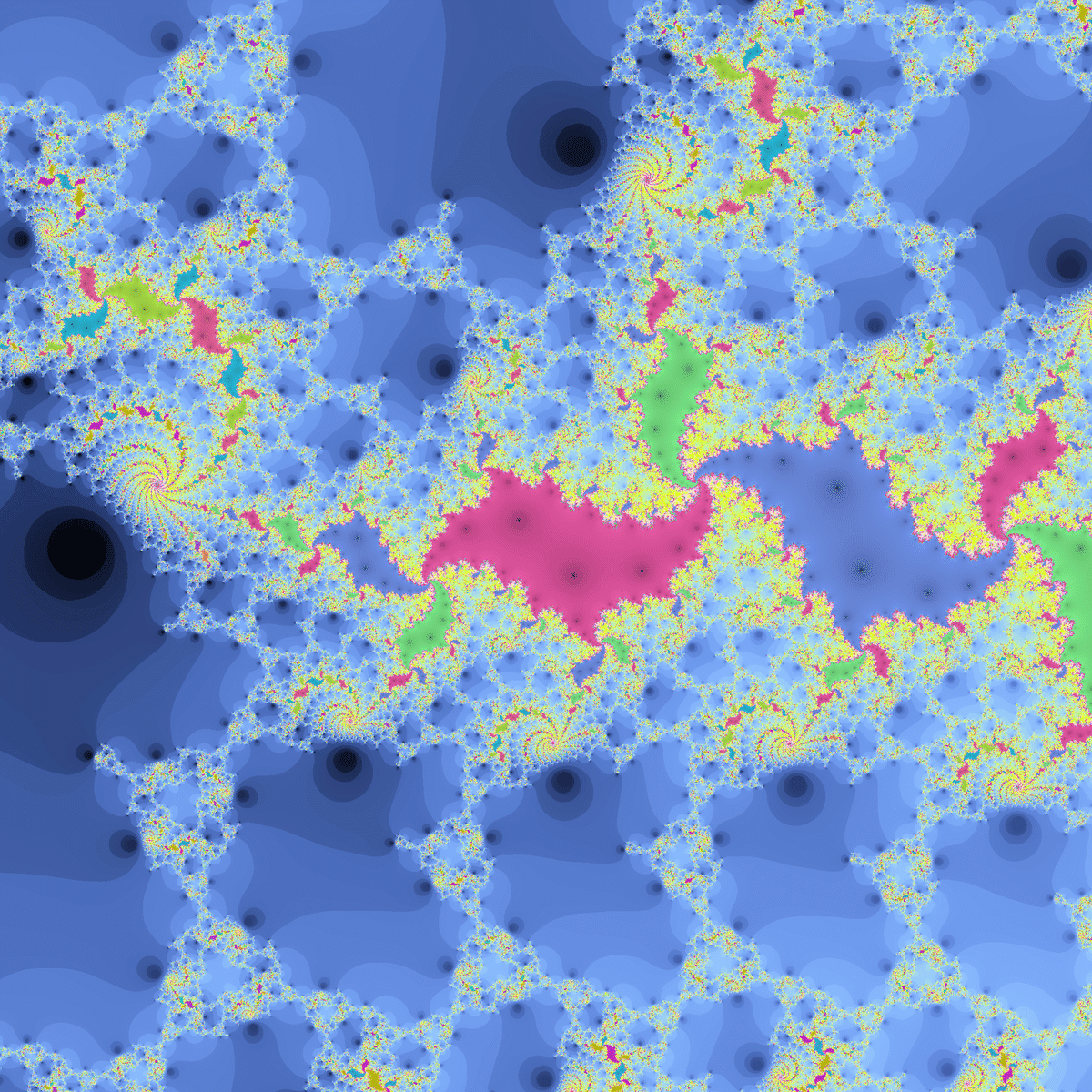



$${c}$$がマンデルブロ集合の収束領域の右下あたり(原点の右上あたり)にあると、周期発散関数のような網目状の模様が出現することがあります。




白領域のあるジュリア集合です。
$${z_0=\pm1}$$のマンデルブロ集合は重なる部分が無いようで、$${z_0=-1}$$に対応する収束領域が$${z_0=1}$$の領域と同時に存在することは起こり得ないようです。


変な領域(っぽいもの)があるジュリア集合です。





いつものです。

無限周期と思しきジュリア集合です。
z_0=0

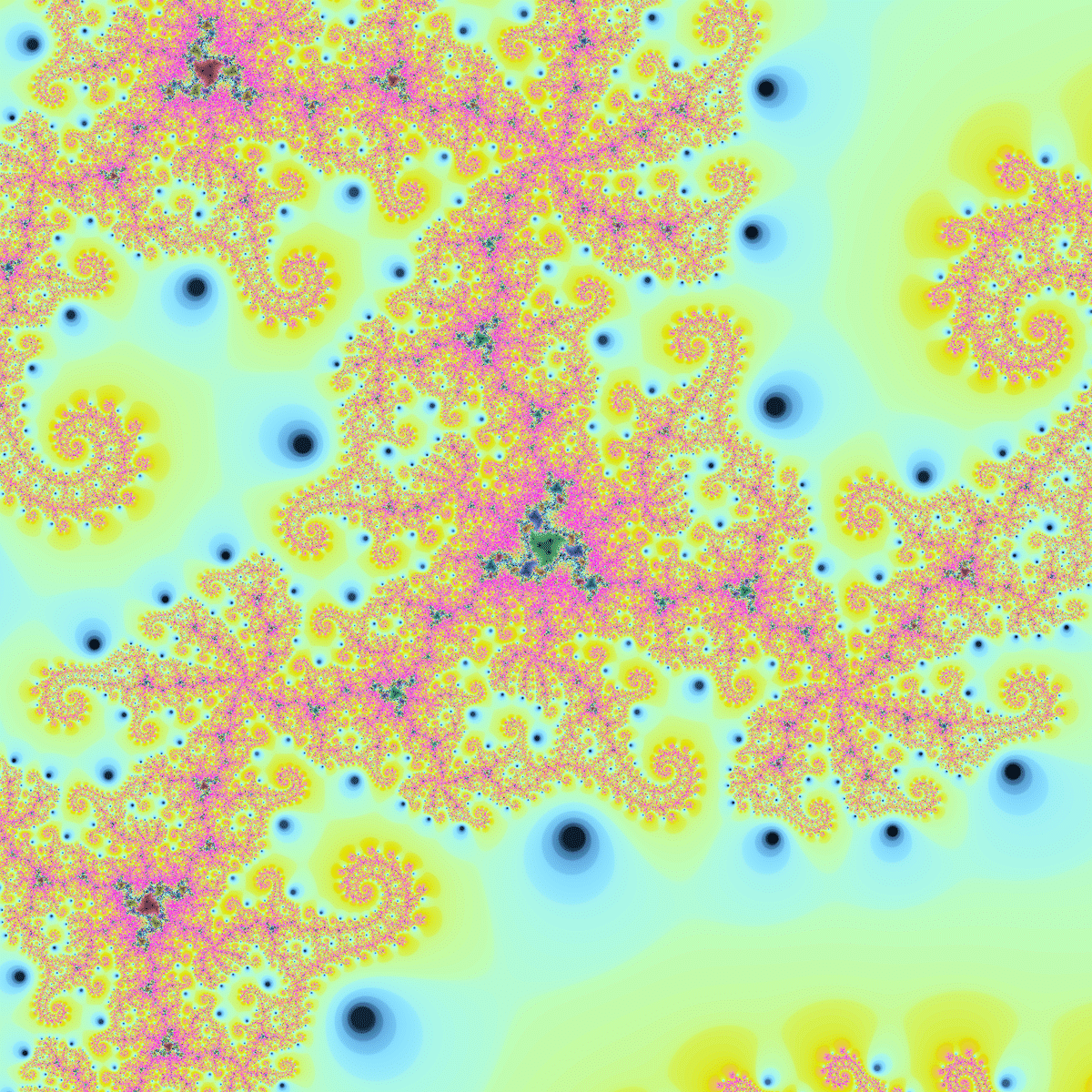

$${z=0}$$は2重臨界点になっているため、$${z^3+c}$$のジュリア集合のような三角形の収束領域を持つジュリア集合が多いです。



以前の記事で言及した、環状に連なった収束領域を持つジュリア集合です。
周期はそれぞれ31、41、85で、奇数周期なのに2つの収束領域が1点で繋がる箇所があるのがわかると思います。





アレです。
