見出し画像

Processingでマンデルブロ集合を描く

108Hassium

どうも、108Hassiumです。

以前から何度か自作のフラクタル図形生成プログラムを紹介する記事を書いてきましたが、応用的な話ばかり載せて基礎的な話はしてなかったことに気付きました。

※☟過去記事

というわけで、この記事ではマンデルブロ集合を例としてProcessingでフラクタル図形を描画する方法を基礎から解説しようと思います。

※私の過去記事は読んでない前提で解説しますが、Processingの文法は学習済みであるものとしています。

定義と計算法

まずはマンデルブロ集合の定義と、プログラムに落とし込んだ場合の計算方法を説明します。

マンデルブロ集合は、以下の数列が無限大に発散しないような複素数$${c}$$の集合です。

  • $${z_0=0}$$

  • $${z_{n+1}=z_n^2+c}$$

※私が書いた他の記事では違う定義を採用していて、上記のものは「$${z^2+c}$$のマンデルブロ集合」と呼んでいます。他の記事での定義の方が便利なのですが、こっちの定義の方が正式なものらしいのでこの記事ではこの定義を用います。

この数列を使って、以下のような手順によりマンデルブロ集合(の近似図)をを描画できます。

  1. 複素平面上の描画したい範囲を決める。(実部と虚部が-2～2の範囲にするとマンデルブロ集合全体がちょうど収まる)

  2. 描画する範囲を格子状に区切る。

  3. 1個ずつのマス目の中(カドとかでもいい)の中から複素数を1点取り、その値を$${c}$$として$${z_n}$$を計算する。

  4. $${z_n}$$が無限大に発散したかどうかでマス目を色分けする。

☝計算法の概要

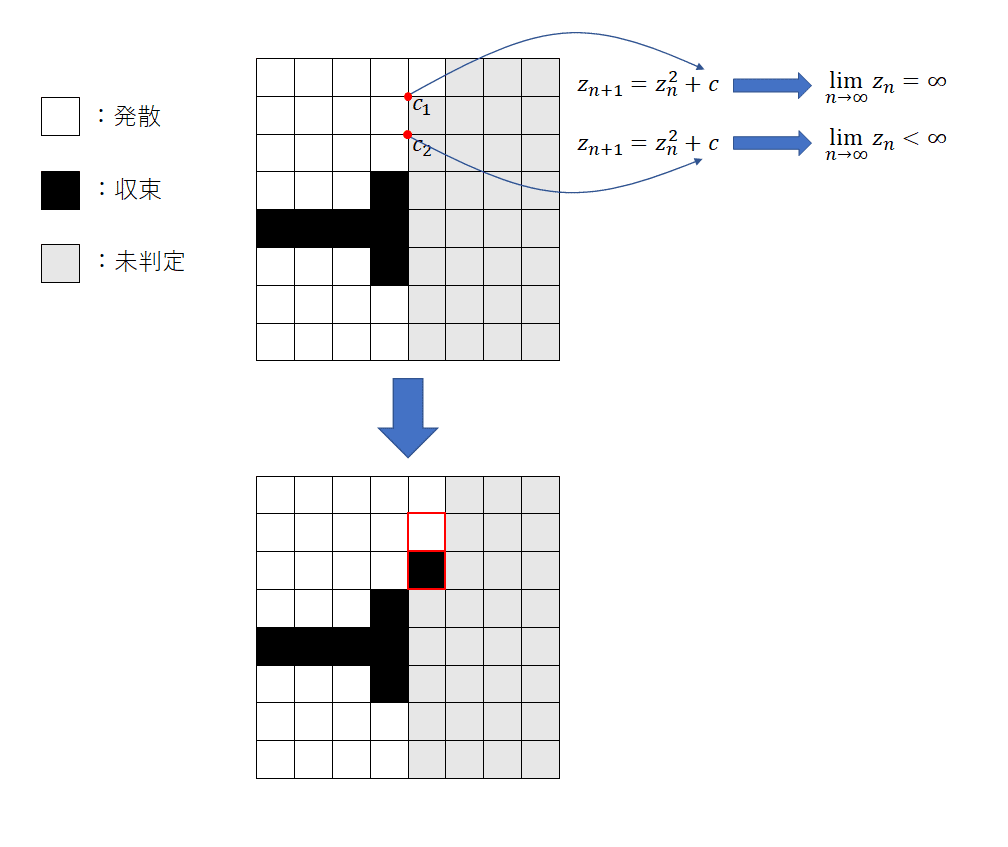
Processingでは複素数を直接計算することはできないっぽいので、$${z_n}$$を計算するときは実部と虚部に分けて実数の計算に落とし込みます。

$${z_n=x_n+y_ni}$$、$${c=a+bi}$$とすると、$${z_{n+1}}$$の実部と虚部は以下のように計算できます。

$${\begin{cases}x_{n+1}=x_n^2-y_n^2+a\\y_{n+1}=2x_ny_n+b\end{cases}}$$

$${\displaystyle{\lim_{n→\infty}}z_n}$$が無限大に発散するかどうかは、以下の定理で判定できます。

$${|z_m|>2}$$を満たす$${m}$$が存在すれば、$${\displaystyle{\lim_{n→\infty}}z_n}$$は必ず無限大に発散する。

※証明は省略します。

$${|z_n|=\sqrt{x_n^2+y_n^2}}$$なので、実際には$${x_n}$$と$${y_n}$$を1項ずつ計算して$${x_n^2+y_n^2}$$が1回でも4を超えたら発散すると判定できます。

ただし、$${|z_m|>2}$$を満たす$${m}$$の大きさは$${c}$$の値次第でいくらでも大きくなるので、実際に計算する際は計算回数の上限を適当に決めて上限に到達したら収束したと見做します。

以上をまとめると、以下のような手順でマンデルブロ集合が描画できることになります。

  1. 複素平面上の描画したい範囲を決める。

  2. 描画する範囲を格子状に区切る。

  3. 計算回数の上限を決める。

  4. 1個ずつのマス目の中の中から複素数を1点取り、その値を$${a+bi}$$として$${x_n}$$と$${y_n}$$と$${x_n^2+y_n^2}$$を計算する。

  5. 計算回数の上限に到達するまでに$${x_n^2+y_n^2}$$が4を超えたかどうかでマス目を色分けする。

実際のコード

先程の説明になるべく忠実に書くと、以下のようなコードが出来上がります。

void setup(){
  size(2000,2000);
  background(0);
  noStroke();
  double x,y,px,py,a,b;
  boolean o;
  for(int k=0;k<2000;k++){
    for(int m=0;m<2000;m++){
      a=(double)k/500.0-2.0;
      b=(double)m/500.0-2.0;
      x=0;
      y=0;
      o=true;
      for(int n=1;n<=500&&o;n++){
        px=x;
        py=y;
        x=px*px-py*py+a;
        y=2.0*px*py+b;
        if(x*x+y*y>4){
          o=false;
          fill(255);
          rect(k,m,1,1);
        }
      }
    }
  }
}

実行すると以下のような画像が表示されます。

☝生成される画像

このコードだとただ画像を表示するだけですが、以下のように書き換えれば生成された画像の保存ができます。

void setup(){
  size(2000,2000);
  background(0);
  noStroke();
  double x,y,px,py,a,b;
  boolean o;
  for(int k=0;k<2000;k++){
    for(int m=0;m<2000;m++){
      a=(double)k/500.0-2.0;
      b=(double)m/500.0-2.0;
      x=0;
      y=0;
      o=true;
      for(int n=1;n<=500&&o;n++){
        px=x;
        py=y;
        x=px*px-py*py+a;
        y=2.0*px*py+b;
        if(x*x+y*y>4){
          o=false;
          fill(255);
          rect(k,m,1,1);
        }
      }
    }
  }
  save("filename.png");  //ここを追加
}

ソースコードを一旦保存してから実行すると、コードが保存されているフォルダ内に"filename"という名前の画像ファイルが保存されます。

次は、コードの各要素を解説します。

void setup(){
  size(2000,2000);  //描画サイズを2000×2000に設定
  background(0);  //背景を黒に設定
  noStroke();  //長方形を描画するときの枠線を消去
  double x,y,px,py,a,b;  //変数の宣言
  boolean o;  //変数の宣言
  ...
}

初期設定です。

宣言した変数のうちxとyが$${x_{n+1}}$$と$${y_{n+1}}$$に、pxとpyは$${x_n}$$と$${y_n}$$に対応しています。

boolean型のoは、数列が発散するかどうか(=$${x_n^2+y_n^2}$$が4を超えるかどうか)の判定結果を格納するのに使います。

このコードだと全体をsetup関数の中に書いている意味は特にないのですが、後で別の関数を作るのでそのためにわざわざsetup関数を使っています。

...
  for(int k=0;k<2000;k++){
    for(int m=0;m<2000;m++){
      a=(double)k/500.0-2.0;
      b=(double)m/500.0-2.0;
      x=0;
      y=0;
      o=true;
      ...
    }
  }
...

二重for文で格子状に$${a+bi}$$の値を決めるところです。

...
      for(int n=1;n<=500&&o;n++){
        px=x;
        py=y;
        x=px*px-py*py+a;
        y=2.0*px*py+b;
        ...
      }
...

$${z_n}$$を計算する部分です。

計算回数の上限を500回に設定し、上限に到達する以外にもboolean型変数oがfalseになっても数列の計算は停止します。

まずxとyの値をpxとpyに移し、pxとpyを使って新しいxとyを計算しています。

...
        if(x*x+y*y>4){
          o=false;
          fill(255);
          rect(k,m,1,1);
        }
...

発散判定です。

$${x_{n+1}^2+y_{n+1}^2}$$が4を超えたら、まずoをfalseにして計算終了のフラグを立て、fill関数で色を決め、rect関数で1×1の長方形を描画(=マス目を塗りつぶす)します。

前に「発散したかどうかで色分けする」と説明しましたが、発散しないことを判定するのは面倒なので実際は発散したときだけ色を塗っています。(発散しなかった場合は最初に塗った黒い背景が表示される)

ちなみに、このコードではfill関数の中身は毎回同じ値なので、三重for文の外側とかに置いてもいいのですが、後で色を細かく変えるコードの説明をするのであの位置に置いてあります。

カラーリングの変更

fill関数の中身を変更することで、カラーリングを変更できます。

fill(pow(1.0-(float)n/500.0,9)*256);

上記のように変更すると、生成される画像は以下のようになります。

外側の白い領域にグラデーションができ、細かい枝状の構造が現れました。

この他にも面白い彩色方法がたくさんあるので、いくつか紹介します。

メタリック

fill(120+20*(float)y);

金属っぽい見た目になる配色です。

以下のようにアレンジすると違う種類の金属みたいな色になります。

fill(120+20*(float)y,120+20*(float)y,0);


fill(120+20*(float)y,60+10*(float)y,0);

パーリーパーソン

fill((float)(x*x)*64,(float)(y*y)*64,0);

とにかく明るい配色です。

※noteの仕様により、グラデーションが正常に表示されていません。

fill((float)(x*x)*64,0,(float)(y*y)*64);


fill((float)(x*x)*64,(float)(y*y)*64,255);

雪解け

fill(cr(n*7),cr(n*8),cr(n*9));

この彩色関数を使うには、以下の関数をコードの最後に追加する必要があります。

float cr(float n){
  return (n%256)*(256-(n%256))/65;
}

これまでに紹介したものと比べると地味な配色ですが、後で説明するマンデルブロ集合の拡大図の描画において威力を発揮します。

同様に、以下の彩色方法も拡大図の描画に便利なので好みに応じて使い分けるとよいでしょう。

fill(cr(n*9),cr(n*9+85),cr(n*9+170));


fill(cr(n),cr(n*2),cr(n*3));

拡大

マンデルブロ集合の描画の醍醐味といえば、拡大図の描画です。

例えば、$${c=-1.37012+0.009495i}$$付近を100000倍に拡大すると以下のようになります。

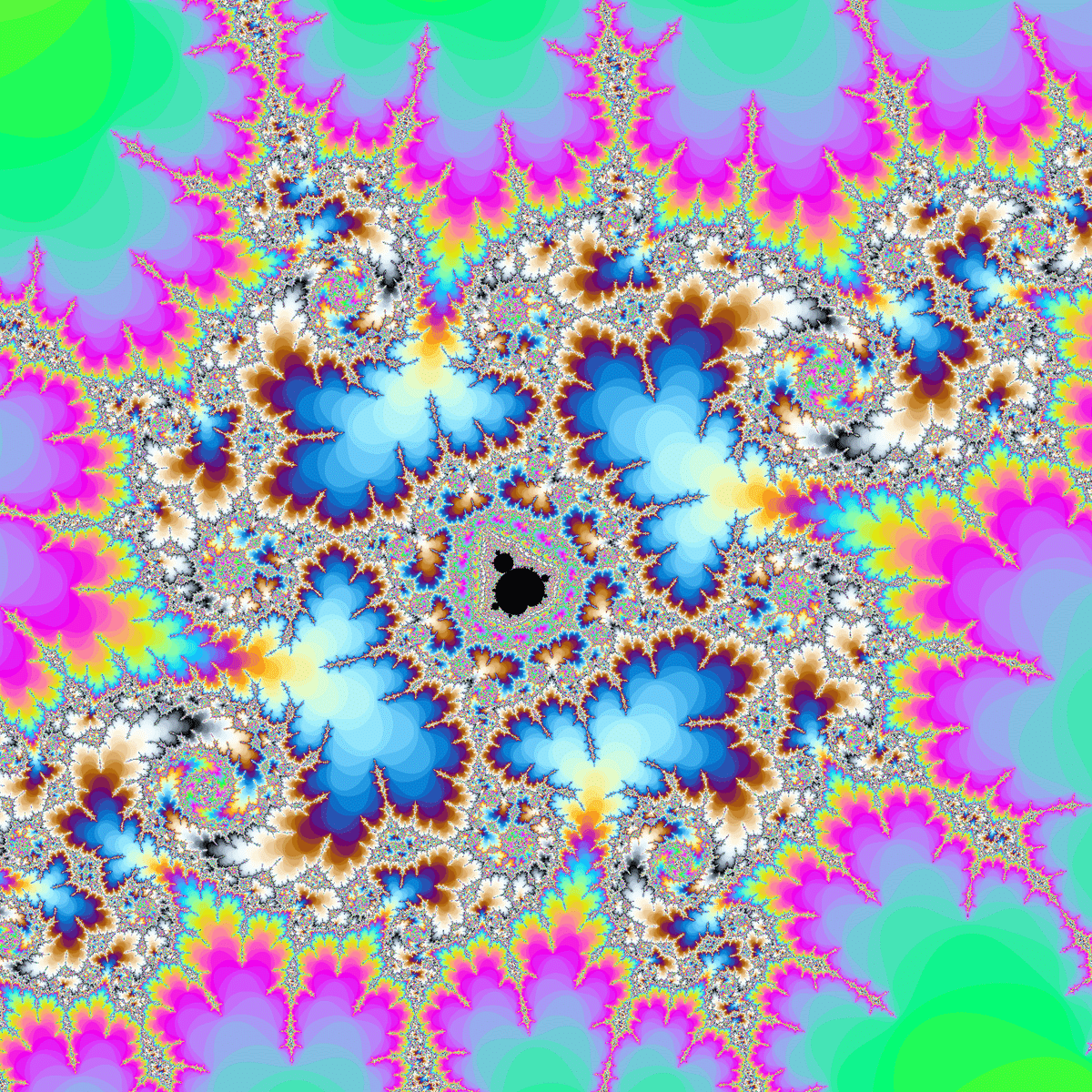
これは以下のコードで描画しました。

void setup(){
  size(2000,2000);
  background(0);
  noStroke();
  double x,y,px,py,a,b,cx,cy,r;
  boolean o;
  r=100000.0;
  cx=-1.37012;
  cy=0.009495;
  for(int k=0;k<2000;k++){
    for(int m=0;m<2000;m++){
      a=(double)k/(1000.0*r)+cx-1.0/r;
      b=(double)m/(1000.0*r)+cy-1.0/r;
      x=0;
      y=0;
      o=true;
      for(int n=1;n<=5000&&o;n++){
        px=x;
        py=y;
        x=px*px-py*py+a;
        y=2.0*px*py+b;
        if(x*x+y*y>4){
          o=false;
          fill(cr(n*7),cr(n*8),cr(n*9));
          rect(k,m,1,1);
        }
      }
    }
  }
  save("-1.37012+0.009495,100000.0.png");
}

float cr(float n){
  return (n%256)*(256-(n%256))/65;
}

拡大倍率を表すr、中心座標を表すcxとcyという変数が追加され、nの上限が500から5000に増えています。

計算回数を増やさなかった場合、発散の遅い領域がうまく描画できず以下のようになります。

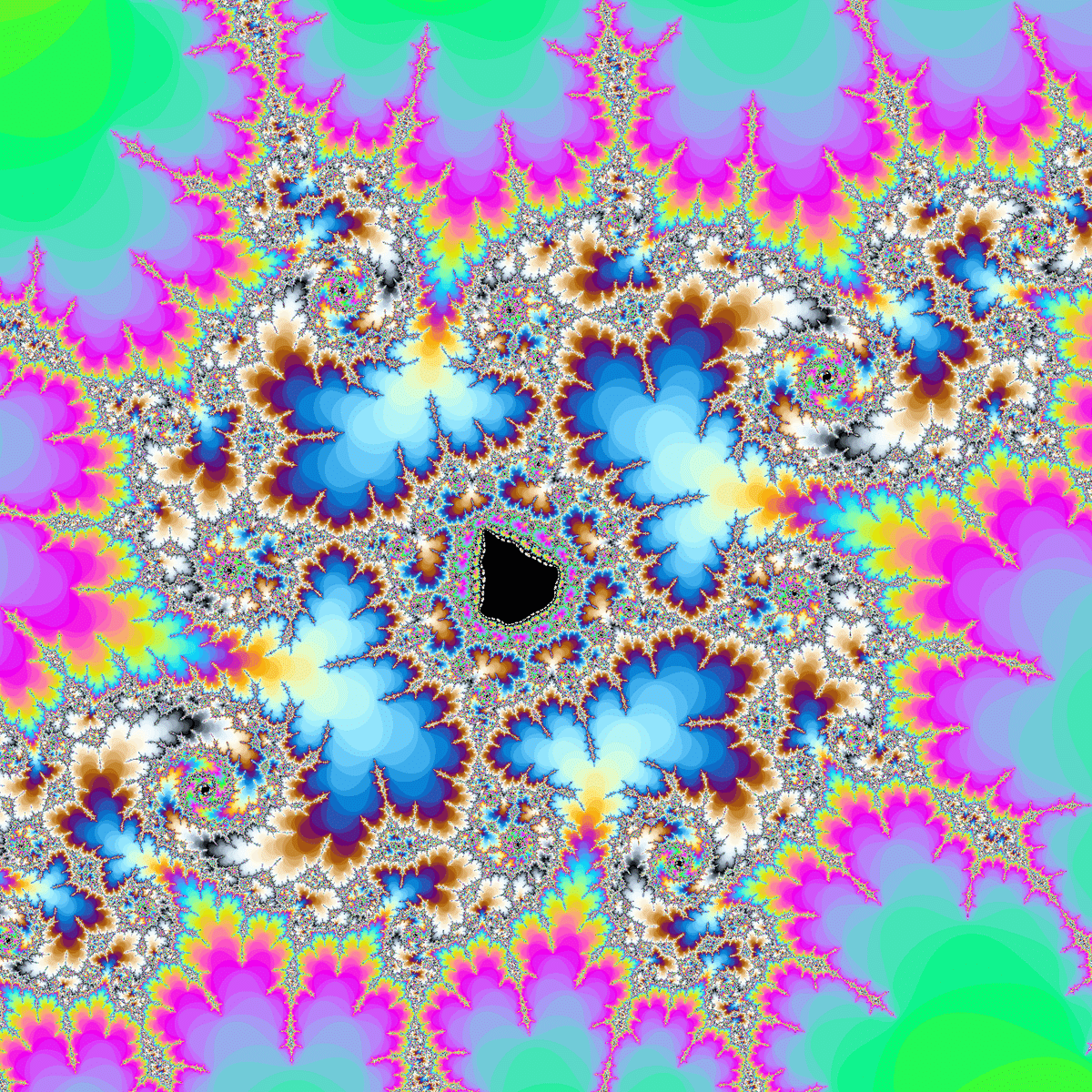
「拡大すると面白い座標」を見つけるには、以下のコードが便利です。

void setup(){
  size(1000,1000);
  background(0);
  noStroke();
  double x,y,px,py,a,b,cx,cy,r;
  boolean o;
  r=1.0;
  cx=0;
  cy=0;
  for(int k=0;k<1000;k++){
    for(int m=0;m<1000;m++){
      if(k==500||m==500){
        fill(255,255,0);
        rect(k,m,1,1);
      }else if(m%50==0||k%50==0){
        fill(255,0,0);
        rect(k,m,1,1);
      }else{
        a=(double)k/(500.0*r)+cx-1.0/r;
        b=(double)m/(500.0*r)+cy-1.0/r;
        x=0;
        y=0;
        o=true;
        for(int n=1;n<=500&&o;n++){
          px=x;
          py=y;
          x=px*px-py*py+a;
          y=2.0*px*py+b;
          if(x*x+y*y>4){
            o=false;
            fill(cr(n*7),cr(n*8),cr(n*9));
            rect(k,m,1,1);
          }
        }
      }
    }
  }
}

float cr(float n){
  return (n%256)*(256-(n%256))/65;
}

これを実行すると、以下のような画面が表示されます。

画面のサイズが2000×2000ではなく1000×1000になり、描画される範囲が実部と虚部が-1～1の範囲になり、20×20のマス目が表示されます。

例えば以下の青丸の位置を拡大するとします。

マス目を数えると、中央から右に4マス、下に2マスの位置にあるのでrとcxとcyを以下のように書き換えます。

  r=10.0;
  cx=0+4.0/10.0;
  cy=0+2.0/10.0;

書き換えてから再度実行すると以下のようになります。

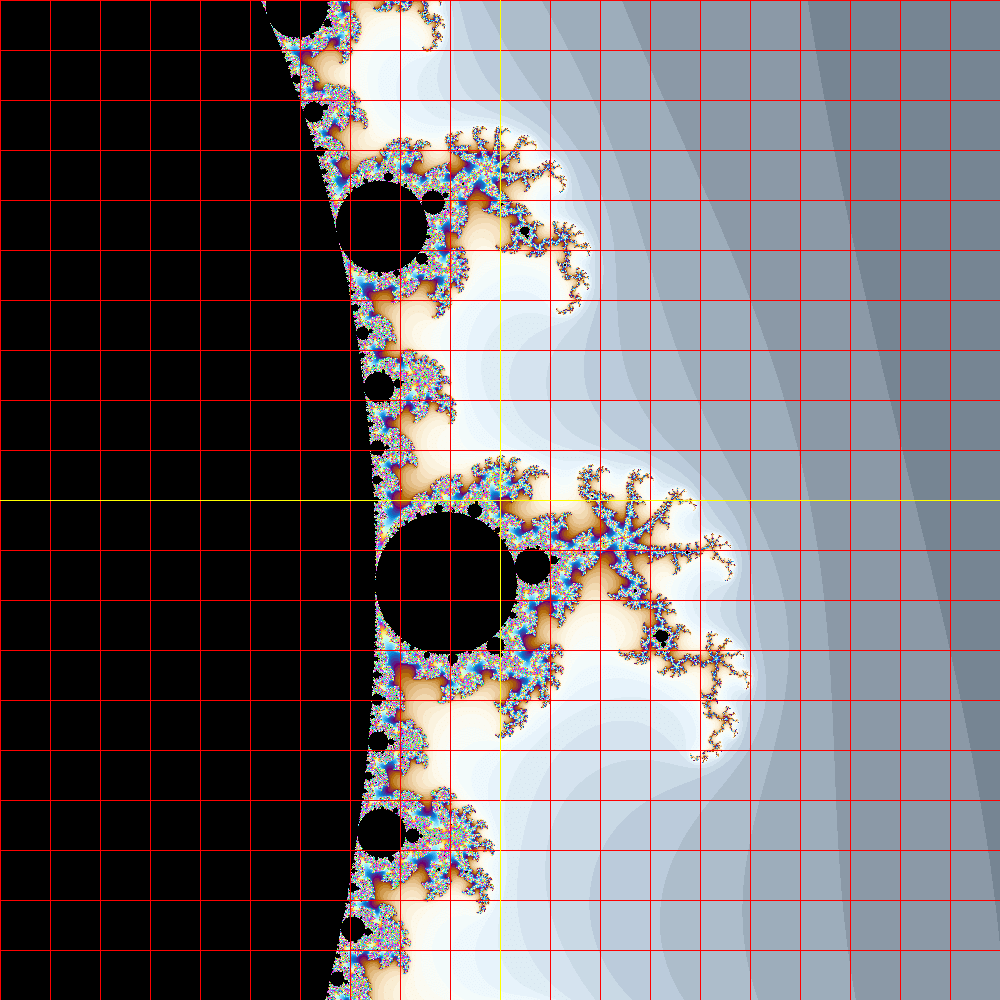
次はここを拡大します。

  r=100.0;
  cx=0+4.0/10.0-1.0/100.0;
  cy=0+2.0/10.0-2.0/100.0;

このように、

  1. rを10倍する

  2. 拡大したい位置の座標÷rをcxとcyにそれぞれ足す

という手順を繰り返し、必要に応じて計算回数を増やすことで、面白い拡大図が得られるパラメータを自由に探すことができます。

ただし、以下の点に注意する必要があります。

  • 座標の横軸は右がプラスだが、縦軸は下がプラスになっている

  • 1000000000倍以上拡大しようとするとcxとcyの変更が正常に反映されなくなる

  • 計算回数を増やしまくると場所によっては描画にかかる時間が非常に長くなる

ちなみに、彩色方法を変えると以下のようになります。

☝fill(cr(n*9),cr(n*9+85),cr(n*9+170));
☝fill(cr(n),cr(n*2),cr(n*3));

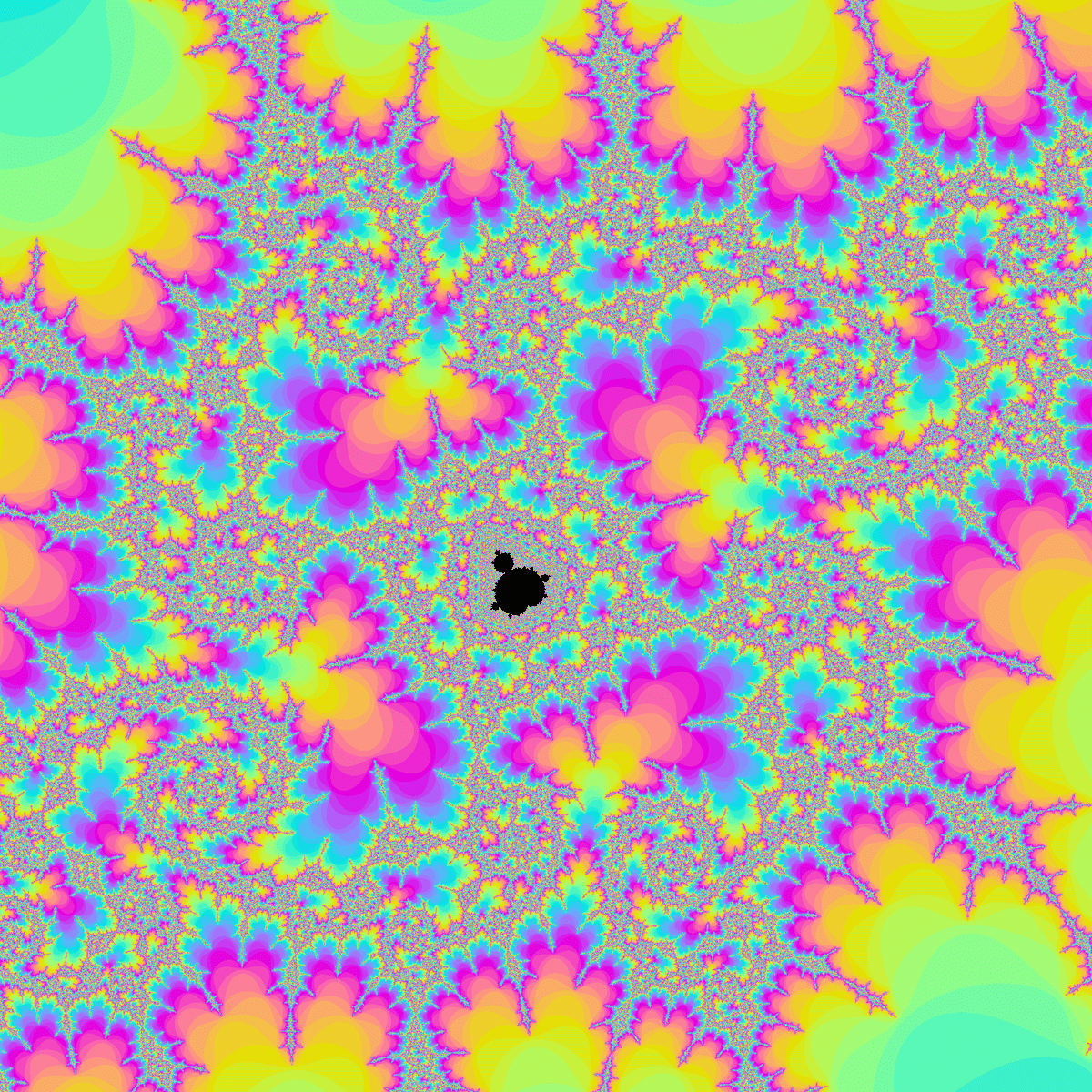
最初に紹介したfill(pow(1.0-(float)n/500.0,9)*256);という彩色法ではnの上限を増やすたびにパラメータを微調整する必要があり、実はcr関数はその問題点を解消するために作った関数です。

pow(1.0-(float)n/500.0,9)*256という関数はnが500を超えると255を超えてしまいますが、cr(n)はnがどれだけ大きくても0～255の範囲に収まるようになっています。

☝fill(120+20*(float)y);

xやyの値を使ったカラーリングでも255オーバー問題は解決できるのですが、マンデルブロ集合本来の線状の構造が見えにくくなってしまいがちなのであまり好きではありません。

計算の高速化

「計算回数を増やすと描画に時間がかかる」とは言いましたが、一応対処法はあります。

void setup(){
  size(2000,2000);
  background(0);
  noStroke();
  double x,y,px,py,a,b,dx=0,dy=0;
  boolean o;
  for(int k=0;k<2000;k++){
    for(int m=0;m<2000;m++){
      a=(double)k/500.0-2.0;
      b=(double)m/500.0-2.0;
      x=0;
      y=0;
      o=true;
      for(int n=1;n<=50000&&o;n++){
        px=x;
        py=y;
        x=px*px-py*py+a;
        y=2.0*px*py+b;
        if(n%100==1){
          dx=x;
          dy=y;
        }else if((x-dx)*(x-dx)+(y-dy)*(y-dy)<1e-10){
          o=false;
        }
        if(x*x+y*y>4){
          o=false;
          fill(cr(n*7),cr(n*8),cr(n*9));
          rect(k,m,1,1);
        }
      }
    }
  }
}

float cr(float n){
  return (n%256)*(256-(n%256))/65;
}

このコードでは計算回数が50000回まで増やされていますが、(私の環境では)500回とほぼ同じように高速で描画できます。

dxとdyという変数が追加され、$${z_n}$$を100回計算するごとに$${z_n}$$の実部と虚部の値が格納され、$${|z_n-(dx+dyi)|^2}$$が1e-10(=$${10^{-10}}$$)未満になったら$${z_n}$$の計算を打ち切る、という処理をしています。

どうやら$${z_n}$$が発散しないときは1周期以上の周期数列に漸近していくらしく、先程のコードでは周期が100未満のときに周期数列に近づいていってるかどうかを判定しています。

拡大図を描画する場合は100以上の周期を持つ領域が描画範囲内に大きく映り込んでいたり閾値が1e-10では精度不足だったりすることがあり、前者の場合は高速化の恩恵が得られず、後者だと誤判定が生じて計算回数を増やした意味がなくなります。

この2点に関しては、それぞれn%100==1の100の部分と1e-10の10を大きい数値に変えることで解決できます。

しかし、パラメータの小細工では解決できない問題もあります。

マンデルブロ集合のフチの辺りは収束が遅く、計算回数を増やすとどうしても計算に時間がかかってしまいます。

☝赤い領域はn<50000で収束判定に引っかからない領域で、中央付近の帯状の部分が収束が遅すぎて判定できなかった部分

マンデルブロ集合以外の図形

コードを少し書き換えるだけで、マンデルブロ集合以外のフラクタル図形も描画できます。

マルチブロ集合

☝3次のマルチブロ集合
void setup(){
  size(2000,2000);
  background(0);
  noStroke();
  double x,y,px,py,a,b;
  boolean o;
  for(int k=0;k<2000;k++){
    for(int m=0;m<2000;m++){
      a=(double)k/500.0-2.0;
      b=(double)m/500.0-2.0;
      x=0;
      y=0;
      o=true;
      for(int n=1;n<=500&&o;n++){
        px=x;
        py=y;
        x=px*px*px-3.0*px*py*py+a;//ここを変える
        y=3.0*px*px*py-py*py*py+b;//ここを変える
        if(x*x+y*y>4){
          o=false;
          fill(cr(n*7),cr(n*8),cr(n*9));
          rect(k,m,1,1);
        }
      }
    }
  }
}

float cr(float n){
  return (n%256)*(256-(n%256))/65;
}

$${d}$$次のマルチブロ集合は、$${z_0=0,z_{n+1}=z_n^d+c}$$という数列が無限大に発散しないような定数$${c}$$の集合です。

$${d=2}$$だと普通のマンデルブロ集合になり、$${d>3}$$のときもマンデルブロ集合と同様に拡大すると綺麗な画像が得られます。

☝d=3,cx=0.18012,cy=1.06034i,r=100000.0

バーニングシップフラクタル

void setup(){
  size(2000,2000);
  background(0);
  noStroke();
  double x,y,px,py,a,b;
  boolean o;
  for(int k=0;k<2000;k++){
    for(int m=0;m<2000;m++){
      a=(double)k/500.0-2.0;
      b=(double)m/500.0-2.0;
      x=0.3;
      y=0.5;
      o=true;
      for(int n=1;n<=500&&o;n++){
        px=abs(x);//ここを変更
        py=abs(y);//ここを変更
        x=px*px-py*py+a;
        y=2.0*px*py+b;
        if(x*x+y*y>4){
          o=false;
          fill(cr(n*7),cr(n*8),cr(n*9));
          rect(k,m,1,1);
        }
      }
    }
  }
}

float cr(float n){
  return (n%256)*(256-(n%256))/65;
}

double abs(double x){//ここから追加
  if(x<0){
    return -x;
  }else{
    return x;
  }
}

バーニングシップフラクタルは、マンデルブロ集合の計算に使う数列を$${z_{n+1}=(|Re(z_n)|+|Im(z_n)|i)^2+c}$$($${Re(z)}$$と$${Im(z)}$$は$${z}$$の実部と虚部)に変えた際に生成される図形です。

Processingには絶対値を計算する関数が用意されているのですが、double型には対応していないようなので自力で関数を作っています。

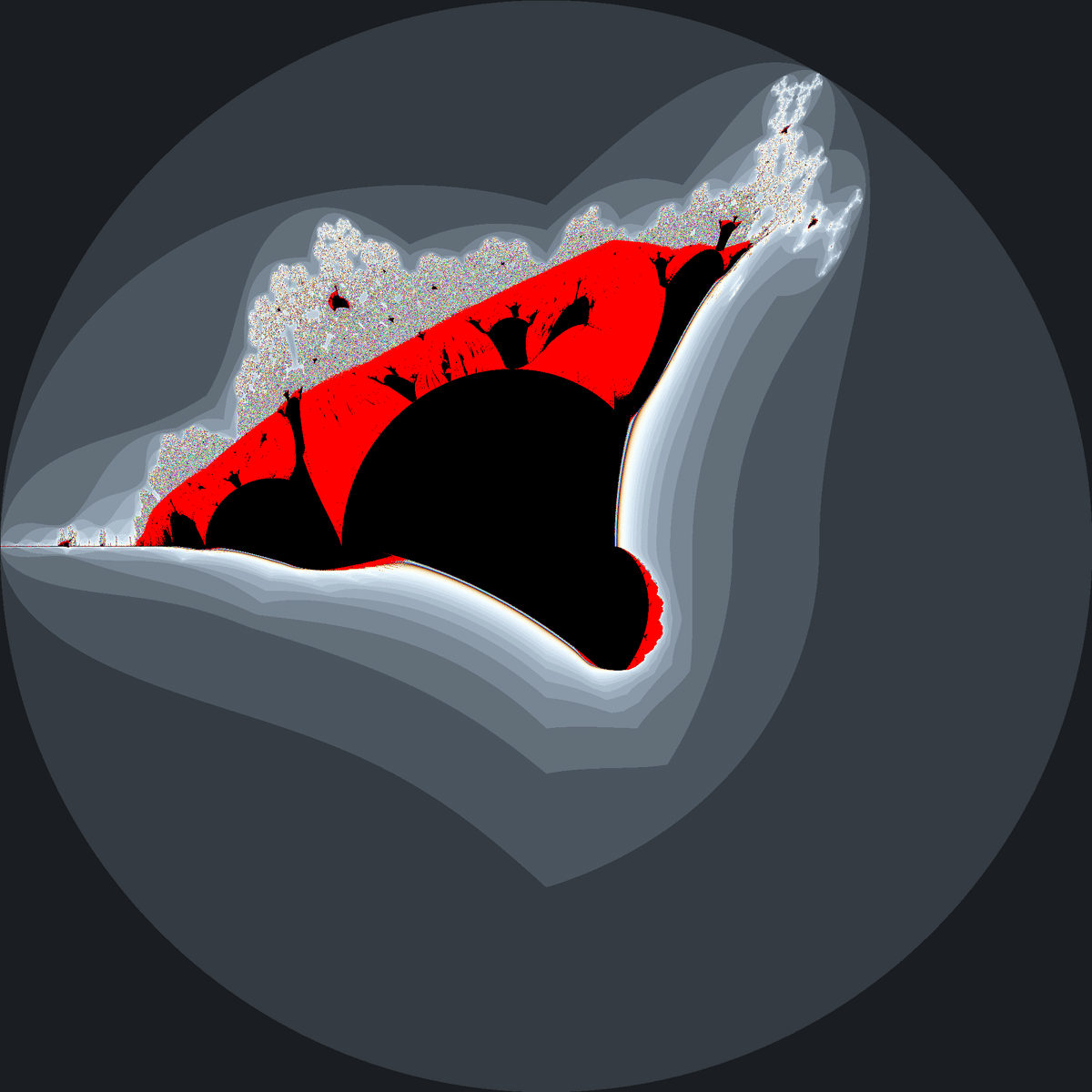
バーニングシップフラクタルは船のような形をしているのが特徴で、左端中央あたりを拡大すると小さい船がたくさん並んでいます。

なお、バーニングシップフラクタルはマンデルブロ集合と違い、計算の高速化がうまくいかない($${z_n}$$が周期数列に収束しない)領域があります。

☝赤が収束判定に引っかからない領域

充填ジュリア集合

☝z^2+0.3+0.5iの充填ジュリア集合
void setup(){
  size(2000,2000);
  background(0);
  noStroke();
  double x,y,px,py,a,b;
  boolean o;
  for(int k=0;k<2000;k++){
    for(int m=0;m<2000;m++){
      //ここから変更
      a=0.3;
      b=0.5;
      x=(double)k/500.0-2.0;
      y=(double)m/500.0-2.0;
      //ここまで変更
      o=true;
      for(int n=1;n<=500&&o;n++){
        px=x;
        py=y;
        x=px*px-py*py+a;
        y=2.0*px*py+b;
        if(x*x+y*y>4){
          o=false;
          fill(cr(n*7),cr(n*8),cr(n*9));
          rect(k,m,1,1);
        }
      }
    }
  }
}

float cr(float n){
  return (n%256)*(256-(n%256))/65;
}

$${f(z)}$$の充填ジュリア集合とは、$${z_{n+1}=f(z_n)}$$という数列が無限大に発散しないような初期値$${z_0}$$の集合です。

aとbの値や$${z_n}$$の式に対応する部分を変更することで、違った見た目のジュリア集合を生成することができます。

☝z^2-0.75+0.1iの充填ジュリア集合
☝z^3+0.6+0.3iの充填ジュリア集合☝z^2-0.75+0.1iの充填ジュリア集合
☝z^3+0.01+0.77iの充填ジュリア集合
☝(|Re(z)|+|Im(z)|i)^2+0.7-1.1iの充填ジュリア集合
☝(|Re(z)|+|Im(z)|i)^2+0.3iの充填ジュリア集合(cx=0.6,cy=0,r=5.0)