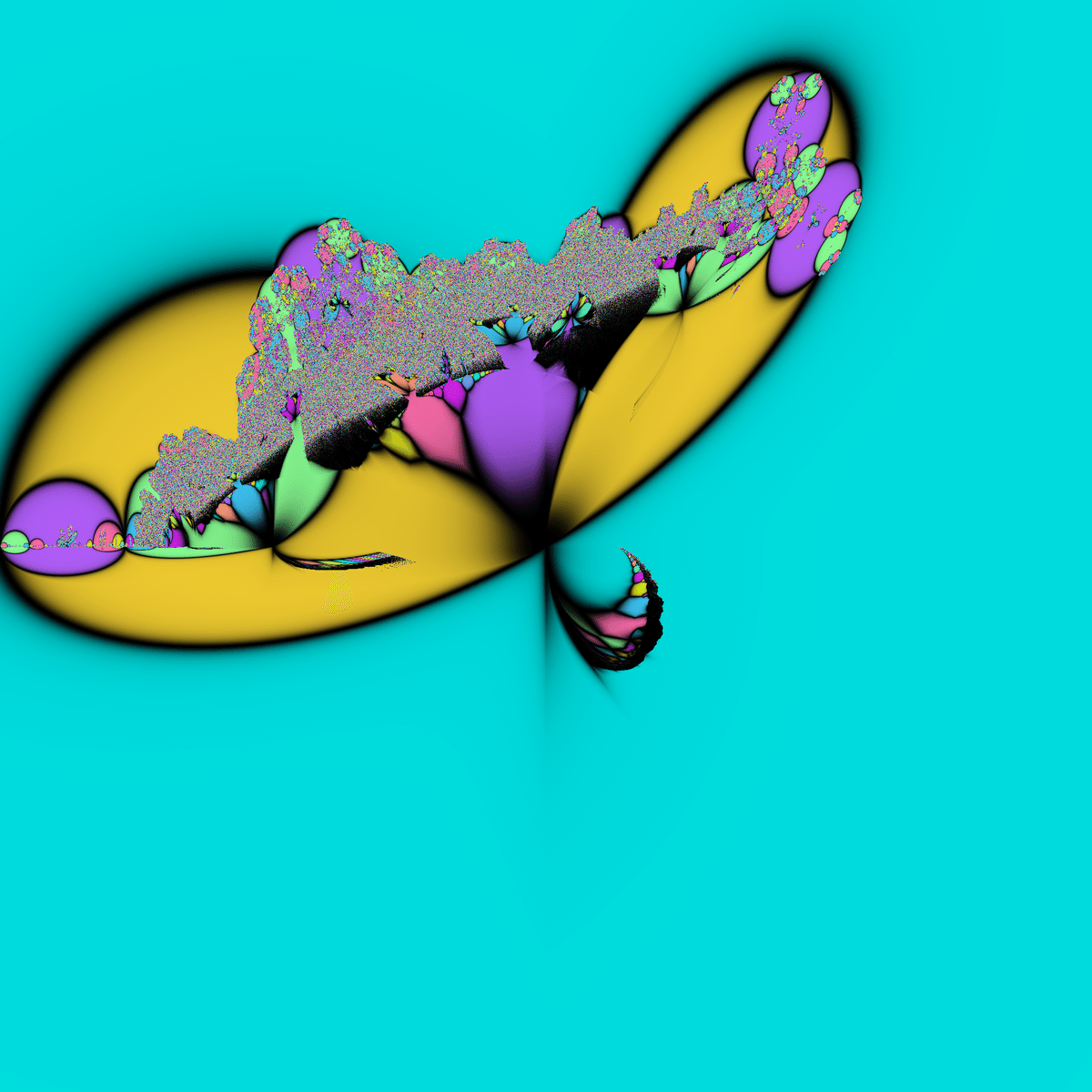どうも、108Hassiumです。
前回の記事ではタイトルに反してあまり遊べていなかった気がするので、orbit trap系の彩色法で遊びまくってみました。
※☟前回
点トラップ
 ☝z^2+ixy+cのマンデルブロ集合(トラップ:0)
☝z^2+ixy+cのマンデルブロ集合(トラップ:0) ☝con(z)^2+cのマンデルブロ集合(トラップ:0)
☝con(z)^2+cのマンデルブロ集合(トラップ:0)※$${\text{con}(x+iy)=x-iy}$$
 ☝B(z)^2+cのマンデルブロ集合(トラップ:0)
☝B(z)^2+cのマンデルブロ集合(トラップ:0)※$${B(x+iy)=|x|+i|y|}$$
 ☝B(z)^2+cのマンデルブロ集合(拡大)
☝B(z)^2+cのマンデルブロ集合(拡大)非解析関数のマンデルブロ集合です。
$${\text{con}(z)^2+c}$$の中央の三角形のフチのような滑らかな境界線は、orbit trapでは描画されないことがあるようです。
 ☝z^2+cのマンデルブロ集合(トラップ:1,i,距離関数:|x|+|y|)
☝z^2+cのマンデルブロ集合(トラップ:1,i,距離関数:|x|+|y|) ☝z^2-1.25+0.02iのジュリア集合(トラップ:0,距離関数:|x^2-y^2|+|2xy|)
☝z^2-1.25+0.02iのジュリア集合(トラップ:0,距離関数:|x^2-y^2|+|2xy|) ☝z^2+cのマンデルブロ集合(トラップ:0,距離関数:x^2+y^2+1.9xy)
☝z^2+cのマンデルブロ集合(トラップ:0,距離関数:x^2+y^2+1.9xy)距離関数を変えてみました。
 ☝z^2+cのマンデルブロ集合(トラップ:c/2)
☝z^2+cのマンデルブロ集合(トラップ:c/2) ☝z^2+cのマンデルブロ集合(トラップ:(1+i)c)
☝z^2+cのマンデルブロ集合(トラップ:(1+i)c) ☝z^2+cのマンデルブロ集合(トラップ:a+ai)
☝z^2+cのマンデルブロ集合(トラップ:a+ai)※$${c=a+bi}$$
 ☝z^2+cのマンデルブロ集合(トラップ:a+a^2i)
☝z^2+cのマンデルブロ集合(トラップ:a+a^2i)トラップとなる点が$${c}$$に依存して動くようにしてみました。
どうやらトラップを$${a+f(a)i}$$という形で表せる点にすると、$${y=f(x)}$$のグラフの曲線が現れて線トラップっぽい見た目になるようです。
線トラップ
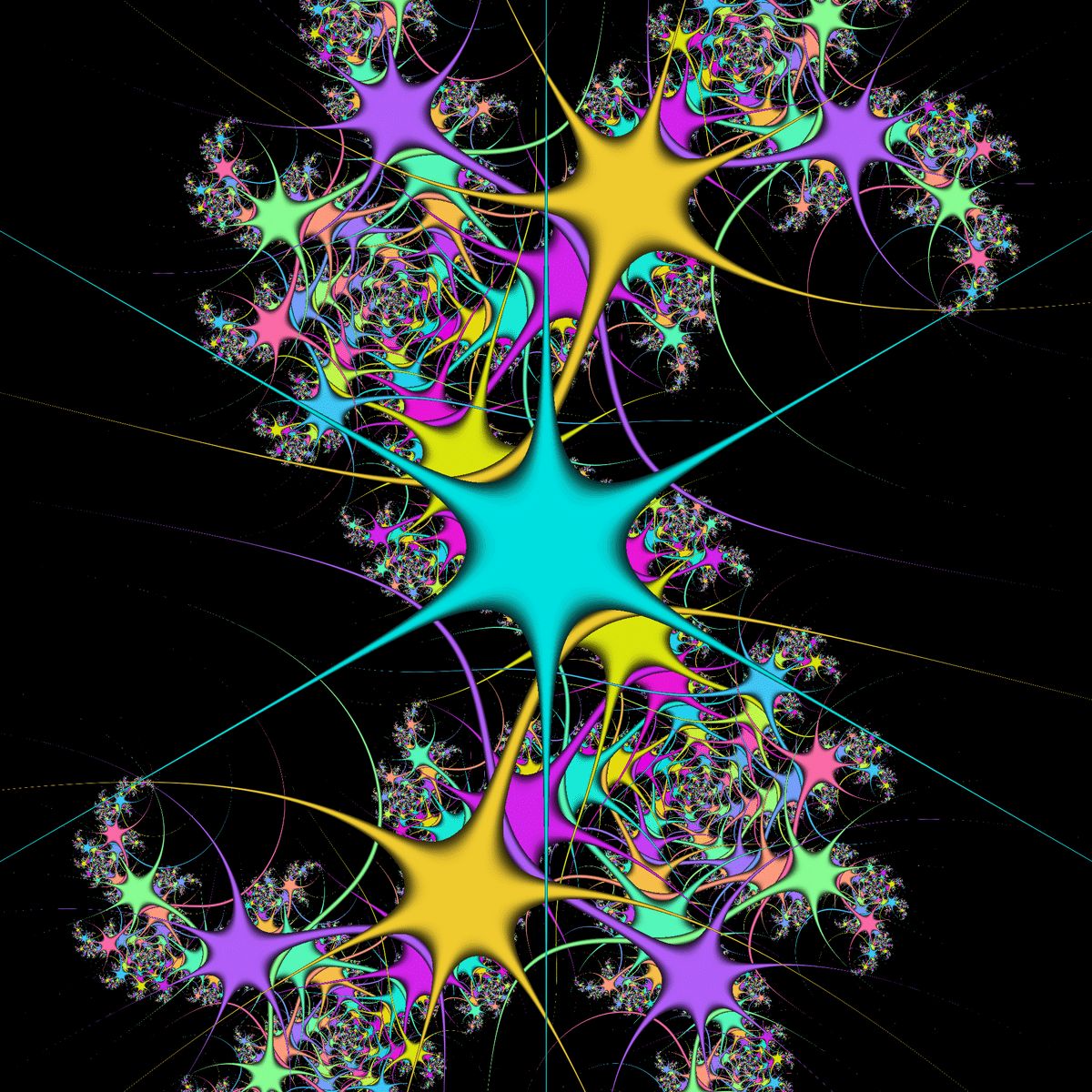 ☝z^2+0.4+0.2iのジュリア集合(トラップ:x^3-3xy^2=0)
☝z^2+0.4+0.2iのジュリア集合(トラップ:x^3-3xy^2=0) ☝z^2-0.4+0.6iのジュリア集合(トラップ:y-sin(x)=0)
☝z^2-0.4+0.6iのジュリア集合(トラップ:y-sin(x)=0)疑似立体化を使うと、適度にキモい画像が簡単に作れます。
 ☝z^2+cのマンデルブロ集合(トラップ:(x-a)^2+(y-b)^2-1=0)
☝z^2+cのマンデルブロ集合(トラップ:(x-a)^2+(y-b)^2-1=0) ☝z^2+cのマンデルブロ集合(トラップ:(x-px)^2+(y-py)^2-1=0)
☝z^2+cのマンデルブロ集合(トラップ:(x-px)^2+(y-py)^2-1=0)※$${z_{n-1}=px+ipy}$$
 ☝z^2-0.5+0.6iのジュリア集合(トラップ:(x-px)^2+(y-py)^2-1=0)
☝z^2-0.5+0.6iのジュリア集合(トラップ:(x-px)^2+(y-py)^2-1=0)線トラップのトラップを動かすと、トラップの形状と大きく異なる線が現れることがあるようです。
Cellular coloring
 ☝(x^2+y^2-1.2,2xy)のジュリア集合(トラップ:(0,0))
☝(x^2+y^2-1.2,2xy)のジュリア集合(トラップ:(0,0)) ☝(x^2+y^2-1.3,2xy)のジュリア集合(トラップ:(0,0))
☝(x^2+y^2-1.3,2xy)のジュリア集合(トラップ:(0,0)) ☝(x+y+1.5,xy-1.9)のジュリア集合(トラップ:(-1,-1))
☝(x+y+1.5,xy-1.9)のジュリア集合(トラップ:(-1,-1)) ☝(x+y+0.6,xy-0.2)のジュリア集合(トラップ:(-1,-1))
☝(x+y+0.6,xy-0.2)のジュリア集合(トラップ:(-1,-1))非解析関数のジュリア集合です。
 ☝z^3+0.43+0.58iのジュリア集合(トラップ:0)
☝z^3+0.43+0.58iのジュリア集合(トラップ:0) ☝(0.9+0.1i)(z^2/2+1/z)のジュリア集合(トラップ:1)
☝(0.9+0.1i)(z^2/2+1/z)のジュリア集合(トラップ:1) ☝z^3/(z+0.1i)+0.2-0.5iのジュリア集合(トラップ:0)
☝z^3/(z+0.1i)+0.2-0.5iのジュリア集合(トラップ:0)複数の吸引的サイクルが存在するジュリア集合の場合、収束先のサイクルによって違う模様が現れるようです。
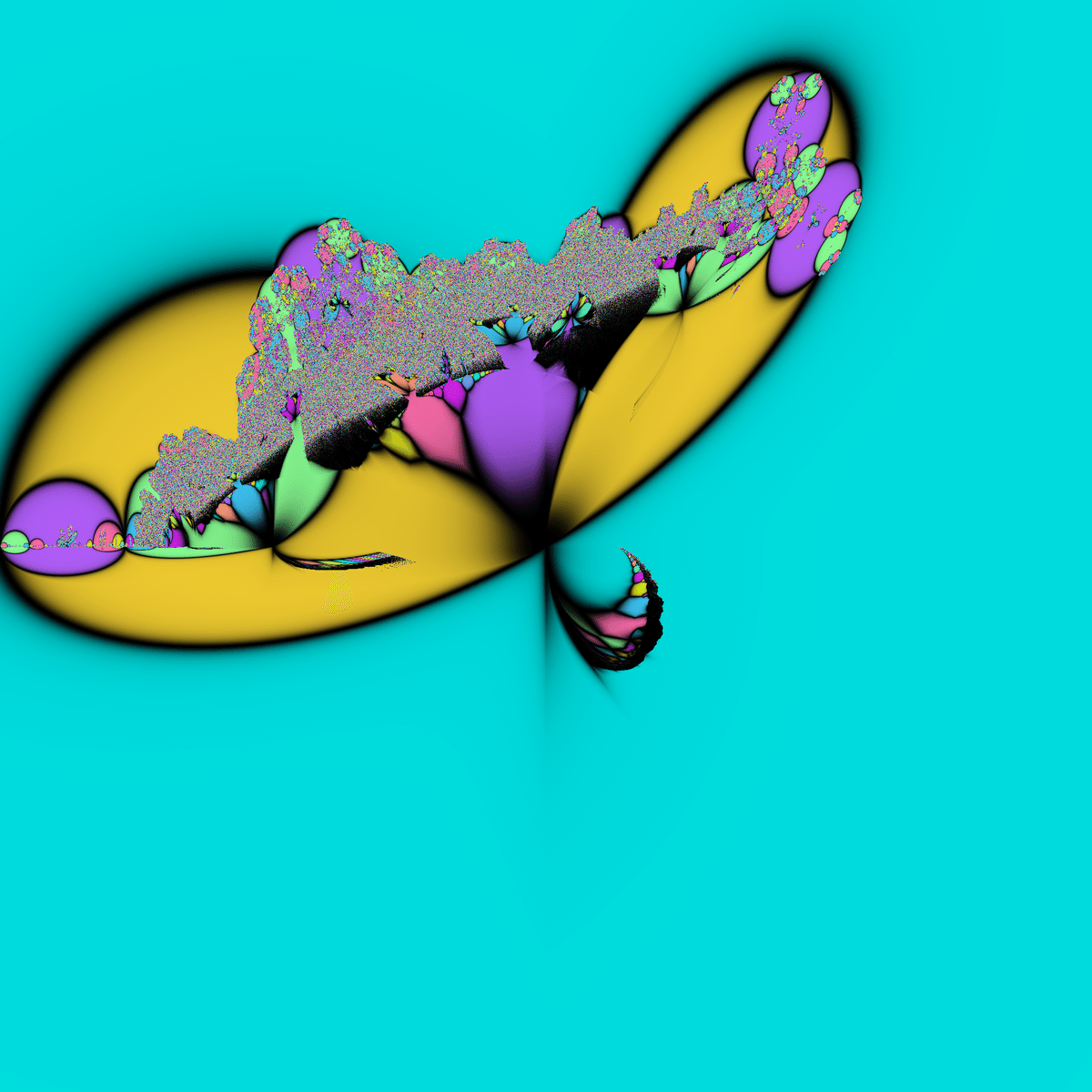 ☝B(z)^2+cのマンデルブロ集合(トラップ:0)
☝B(z)^2+cのマンデルブロ集合(トラップ:0) ☝c(z+1/z)のマンデルブロ集合(トラップ:1)
☝c(z+1/z)のマンデルブロ集合(トラップ:1) ☝c(z+1/z)のマンデルブロ集合(トラップ:-1)
☝c(z+1/z)のマンデルブロ集合(トラップ:-1)$${z_n}$$が非周期的になる領域は、cellular coloringではノイズ状に描画されるようです。
 ☝c/(z^2-1)+1のマンデルブロ集合(トラップ:0)
☝c/(z^2-1)+1のマンデルブロ集合(トラップ:0) ☝(-0.2+0.7i)/(z^2-1)+1のジュリア集合(トラップ:0)
☝(-0.2+0.7i)/(z^2-1)+1のジュリア集合(トラップ:0)周期発散関数の場合、発散領域がうまく描画できないときがあるようです。
 ☝z^2+cのマンデルブロ集合(トラップ:c/2)
☝z^2+cのマンデルブロ集合(トラップ:c/2) ☝z^2+cのマンデルブロ集合(トラップ:(1+i)c)
☝z^2+cのマンデルブロ集合(トラップ:(1+i)c) ☝z^2+cのマンデルブロ集合(トラップ:a+a^2i)
☝z^2+cのマンデルブロ集合(トラップ:a+a^2i)トラップを動かしたやつです。
 ☝z^2+cのマンデルブロ集合(トラップ:0,距離関数:|x|+|y|)
☝z^2+cのマンデルブロ集合(トラップ:0,距離関数:|x|+|y|) ☝z^2+0.3+0.5iのジュリア集合(トラップ:0,距離関数:|x|+|y|)
☝z^2+0.3+0.5iのジュリア集合(トラップ:0,距離関数:|x|+|y|) ☝z^2+cのマンデルブロ集合(トラップ:0,距離関数:x^2+y^2+1.9xy)
☝z^2+cのマンデルブロ集合(トラップ:0,距離関数:x^2+y^2+1.9xy) ☝z^2-0.6+0.4iのジュリア集合(トラップ:0,距離関数:x^2+y^2+1.9xy)
☝z^2-0.6+0.4iのジュリア集合(トラップ:0,距離関数:x^2+y^2+1.9xy) ☝z^2+0.1+0.6iのジュリア集合(トラップ:0,距離関数:x^2+y^2+1.9xy)
☝z^2+0.1+0.6iのジュリア集合(トラップ:0,距離関数:x^2+y^2+1.9xy)距離関数を変えたやつです。