
ハイブリッドジュリア集合
どうも、Fractal Forumsを眺めるのが日課の108Hassiumです。
Fractal Forumsはその名の通りフラクタル関連の話題が集まるフォーラムで、様々なフラクタル図形の画像や描画方法などが投稿されています。
一年ほど前、こんなポストを発見しました。
このポストでは、「普通のジュリア集合と分解型複素数のジュリア集合を繋いだようなジュリア集合を生成する関数」として$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$という関数を紹介しています。

※他にもいろいろ紹介されているのですが、今回は$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$に話題を絞ります。
一見ただの多項式の組み合わせにしか見えない関数がこのような性質を持つのは、当時の私にとってかなり衝撃的でした。
というわけで、$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$という関数がこのような性質を持つ仕組みや、似たような性質を持つ関数の作り方を探る過程の試行錯誤の様子を紹介したいと思います。
Step0:観察
試行錯誤を始める前に、大本の$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$という関数の性質を調べてみます。







ジュリア集合です。



(±0.8,0)を初期値にすると、それぞれ分解型複素数のものと普通の複素数の$${z^2+c}$$のマンデルブロ集合に似た形のマンデルブロ集合になるようです。
Step1:場合分け
$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$のジュリア集合を観察してみると、「右半分に分解型複素数のジュリア集合があり、左に複素数のジュリア集合がある」という感じの見た目になっているものが多いです。
というわけで、こんなコードを書いてみました。
void setup(){
size(2000,2000);
background(0);
noStroke();
double x,y,px,py,cx,cy;
boolean o;
for(int a=0;a<2000;a++){
for(int b=0;b<2000;b++){
cx=(double)a/500.0-2.0;
cy=(double)b/500.0-2.0;
x=-1.0;
y=0;
o=true;
for(int c=0;c<500&&o;c++){
px=x;
py=y;
if(x<0){
x=px*px-py*py+2.0*px+cx;
y=2.0*px*py+2.0*py+cy;
}else{
x=px*px+py*py-2.0*px+cx;
y=2.0*px*py-2.0*py+cy;
}
if(x*x+y*y>100){
fill(cr(c*7),cr(c*8),cr(c*9));
rect(a,b,1,1);
o=false;
}
}
}
}
}
float cr(float c){
return (c%256)*(256-(c%256))/65;
}※言語はProcessing(参考)
このプログラムでは、以下のような関数のマンデルブロ集合を$${(x_0,y_0)=(-1,0)}$$で描画します。
$${(F(x,y),G(x,y))=\begin{cases}(x^2-y^2+2x+a,2xy+2y+b)&\text{if} x<0\\(x^2+y^2-2x+a,2xy-2y+b)&\text{if} 0\leq x\end{cases}}$$
$${x}$$が負のときの式が普通の複素数の$${z^2+2z+c}$$の式で、もう片方は分解型複素数の$${z^2-2z+c}$$の式です。
以下、このような「$${x<0}$$のときが複素関数、$${0\leq x}$$が分解型複素関数」というような関数を$${(z^2+2z+c|z^2-2z+c)}$$というように表記することにします。
さて、$${(z^2+2z+c|z^2-2z+c)}$$のマンデルブロ集合は以下のようになりました。


真ん中に複素数、右端に分解型複素数のマンデルブロ集合っぽい形が見えますが、分解型複素数の方は何故か中途半端に切れたような形になり、さらに$${\pm1}$$($${z^2\pm2z+c}$$の臨界点)のどちらを初期値にしても同じ見た目のマンデルブロ集合になってしまっています。
ジュリア集合はこんな感じでした。



右半分の領域は一応分解型複素数っぽさはあるものの、$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$とは全然違う感じの見た目になってしまっています。
ところで、さっきのコードでは収束領域の中を彩色する機能は削ってありますが、導入してみたところこんな画像も得られました。


色々と面白い部分があり、特に$${(z^2+2z+0.7|z^2-2z+0.7)}$$のジュリア集合はとても美しくなって驚いたのですが、やはり「$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$みたいな関数を作る」という目的にはそぐわない結果です。
というわけで、似たような関数をいくつか作ってみたところ$${(z^2+2z+c|-z^2+2z+c)}$$がかなり理想に近い結果になりました。



また、$${(z^2+rz+c|-z^2+rz+c)}$$の$${r}$$の値を動かすと以下のようになりました。
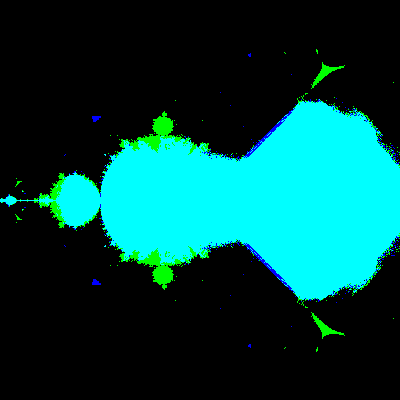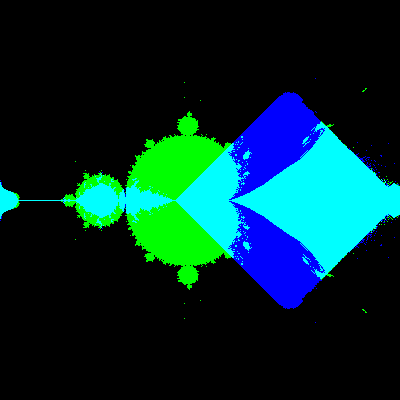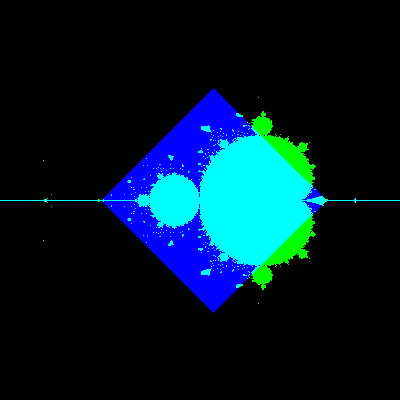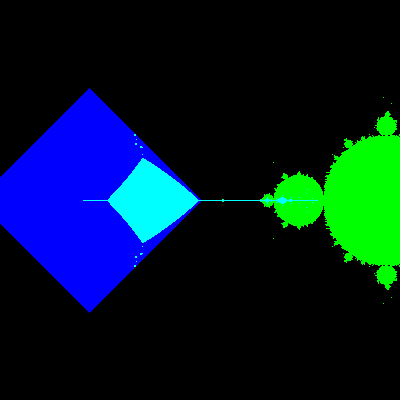
二つのマンデルブロ集合の重なり方を見ると、$${r=2}$$より$${r=3}$$の方がより$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$に近いように見えます。

というわけでジュリア集合も描画してみました。





やはり理想的です。
Step2:絶対値
$${(z^2+3z+c|-z^2+3z+c)}$$のような場合分けのある関数は、絶対値を使って場合分け無しで綺麗に表せることがあります。
実際、$${(-|x|x-y^2+3x+a,-2|x|y+3y+b)}$$という関数を$${x}$$の符号ごとに分けて考えると
$${(-|x|x-y^2+3x+a,-2|x|y+3y+b)=\begin{cases}(x^2-y^2+3x+a,2xy+3y+b)&\text{if} x<0\\(-x^2-y^2+3x+a,-2xy+3y+b)&\text{if} 0\leq x\end{cases}}$$
・・・というようになり、$${(z^2+3z+c|-z^2+3z+c)}$$のxy表現と一致することが確かめられます。
一方、$${(z^2+2z+c|z^2-2z+c)}$$を場合分け無しで表すと以下のようになります。
$${(x^2+\text{sign}(x)y^2-\text{sign}(x)2x+a,2xy-\text{sign}(x)2y+b)}$$
$${\text{sign}(x)}$$は$${x}$$の符号を表し、絶対値関数を使うと$${\frac{|x|}{x}}$$と表せます。

※$${\frac{|x|}{x}}$$は$${x=0}$$では未定義になるのですが、気にしないことにします。
ところで、$${(z^2+2z+c|z^2-2z+c)}$$マンデルブロ集合やジュリア集合には、不自然に切り取られたような箇所が存在していました。


これは不連続な関数から生成されるフラクタル図形によく見られる特徴なのですが、場合分けを使わない表記にしてみると符号関数が出てくるため$${(z^2+2z+c|z^2-2z+c)}$$が不連続であることがわかりやすくなります。
Step3:3次関数
$${(-|x|x-y^2+3x+a,-2|x|y+3y+b)}$$の$${-x|x|+3x}$$の部分のグラフは、こんな形をしています。

2つの放物線を点対象につないだ形なのですが、3次関数のグラフによく似ています。
このことに気付いたとき、「$${-|x|x+3x}$$と$${-2|x|y}$$を多項式関数で上手く近似できれば、絶対値関数を使わずに『複素数と分解型複素数のハイブリット関数』を作れるのではないか」という事を思いつきました。
というわけで、試行錯誤の結果がこちらです。


$${-|x|x+3x}$$が$${\frac{-x^3}{3}+2.25x}$$に、$${-2|x|y}$$が$${-2.25x^2y}$$に置き換わっています。
係数の決定には手探りの微調整が必要で面倒臭いし、結果として得られた係数は中途半端な値で美しくないし、なにより肝心のマンデルブロ集合の見た目が崩れすぎているのが気に入りません。
どうしたものかと考えていたところ、全く違うアプローチを思いつきました。
まず、$${r(-\frac{z^3}{3}+z)+c}$$のマンデルブロ集合は以下のようになります。

$${r(-\frac{z^3}{3}+z)+c}$$の臨界点は±1で、どちらに対応するマンデルブロ集合も$${z^2+c}$$のものに似た形をしていて、$${r}$$の値によって大きさと位置が変化します。
もし2つのマンデルブロ集合のうち一方が分解型複素数のものに変われば、$${(z^2+rz+c|z^2-rz+c)}$$とよく似た関数になります。
というわけで、$${(r(-\frac{z^3}{3}+z)+c|r(-\frac{z^3}{3}+z)+c)}$$のマンデルブロ集合を描画してみました。

予想通り(?)に、$${z_0=1}$$の方のマンデルブロ集合が四角い形になりました。
ということは、$${(r(-\frac{z^3}{3}+z)+c|r(-\frac{z^3}{3}+z)+c)}$$を多項式関数で近似できれば「絶対値関数を使わずに『複素数と分解型複素数のハイブリット関数』を作る」という目的を達成できそうです。
ちなみにマンデルブロ集合の重なり方を見ると、$${r=2}$$とすると$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$や$${(z^2+3z+c|z^2-3z+c)}$$に似た関数になりそうです。
さて、$${(2(-\frac{z^3}{3}+z)+c|2(-\frac{z^3}{3}+z)+c)}$$を場合分け無しで書き直すと以下のようになります。
$${(2(-\frac{x^3}{3}-|x|y^2+x)+a,2(-x^2y-\frac{\text{sign}(x)y^3}{3}+y)+b)}$$
絶対値関数と符号関数がそれぞれ1回ずつ使われているので、両方とも多項式関数による近似ができればよさそうです。
結論から言うと、$${|x|}$$を$${1}$$に、$${\text{sign}(x)}$$は$${0}$$に置き換えると以下のようになります。


$${|x|\approx1}$$、$${\text{sign}(x)\approx0}$$というめちゃくちゃ雑な近似で上手くいく理由はさっぱりわからないのですが、とりあえず上手くいったのでヨシとします。
最後に、$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$の正体(?)について個人的な見解を述べます。
まず、元となった関数は$${2z-z^3+c}$$で、「(±0.8,0)を初期値にするといい感じのマンデルブロ集合になる」の±0.8という値は$${2z-z^3+c}$$の臨界点である$${\pm\frac{\sqrt{6}}{3}}$$(≒±0.816)という値に関係していると考えられます。
そして、私が$${2(-\frac{z^3}{3}+z)+c}$$から$${(2(-\frac{x^3}{3}-y^2+x)+a,2(-x^2y+y)+b)}$$に辿り着いたのと同じ行程を踏むと、$${(2x-x^3-3y^2+a,2y-3x^2y+b)}$$という関数になります。
$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$と見比べると1か所だけ係数が異なり、この違いは$${|x|}$$を1ではなく$${\frac{2}{3}}$$で近似したことに相当します。
もちろんこれは「あのポストの投稿者がこのような思考過程を経て$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$という関数を発見した」という意味ではないのですが、私としては$${(2x-x^3-2y^2+a,2y-3x^2y+b)}$$があのような性質を持つ背景を少し見ることができたような気がするので満足です。
おまけ


考え方的に$${(-z^2-2z+c|z^2-2z+c)}$$とほとんど変わらないのに何故か上手くいかなかったケースです。
左側には普通の複素数のマンデルブロ集合があって右側には分解型複素数のものがある、という性質を持たせることはできているものの、両者の間に謎の収束領域の塊ができてしまっています。



$${2z-\frac{z^3}{6}+c}$$から作った、収束領域のサイズが大きいハイブリッド関数です。



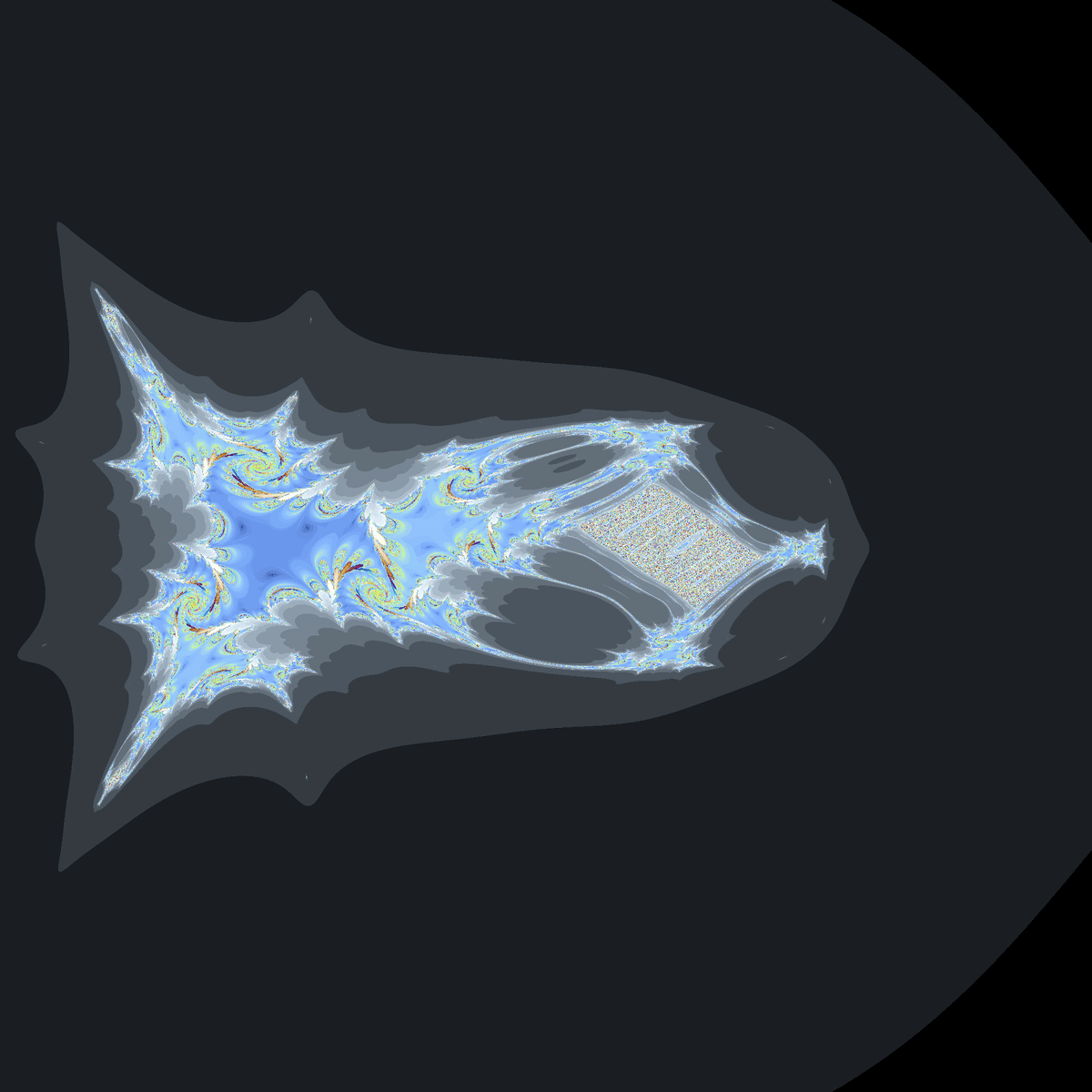

$${-1.2((z+1)^4-2(z+1)^3)+c}$$をもとにした関数です。
「複素数の$${z^3+c}$$と分解型複素数の$${z^2+c}$$のハイブリッド」みたいなものができるんじゃないかと期待したのですが、調整がうまくいきませんでした。
