今週のフラクタル64　((|x|+i(|y+0.5|-0.5))^2+c)

どうも、108Hassiumです。

今回は$${(|x|+i(|y+0.5|-0.5))^2+c}$$に関するフラクタル図形をお届けします。

(|x|+i(|y+0.5|-0.5))^2+c

☝(|x|+i(|y+0.5|-0.5))^2+cのマンデルブロ集合(z_0=0,x=-2~2,y=-3~1)

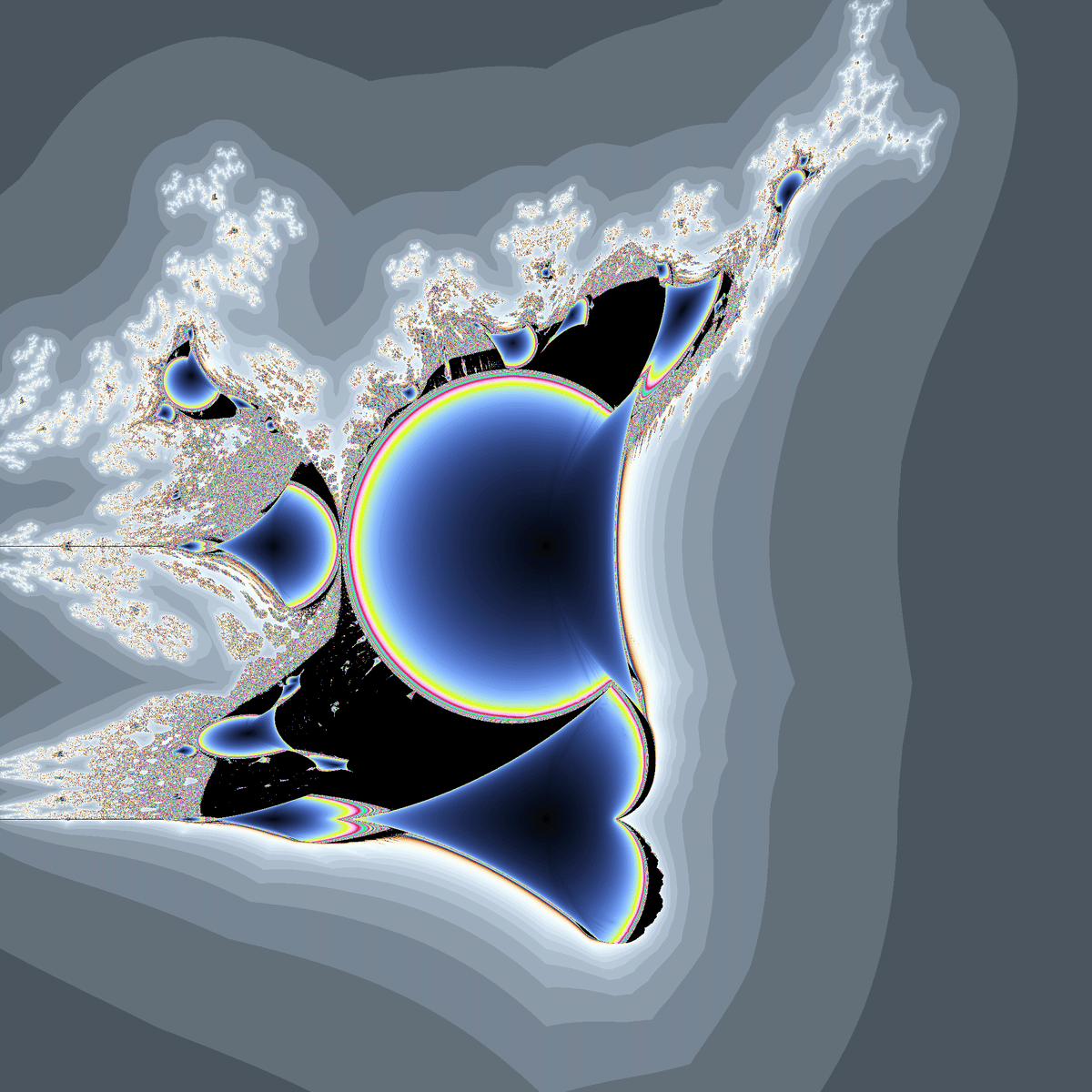
以前「$${z^2+c}$$のマンデルブロ集合と$${\text{con}(z)^2+c}$$のマンデルブロ集合を縦に並べたようなマンデルブロ集合を生成する関数」を紹介したことがありますが、この関数では「heart mandelbrot」と「perpendicular mandelbrot」が同じように並びます。

※☟「$${z^2+c}$$の(中略)する関数」の記事

※☟「heart mandelbrot」と「perpendicular mandelbrot」に関する記事

☝(|x|+i(|y+0.5|-0.5))^2-0.7-0.72iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-0.71-1.31iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-1.48のジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-0.65-0.54iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-0.2-1.66iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2+0.31+0.03iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-0.69-0.72iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-0.69-0.72iのジュリア集合

ジュリア集合は2本の対称軸を持ちますが、水平方向の対称軸は実軸ではなく$${y=-0.5}$$の位置にあります。(この性質も$${(x+i(|y+0.5|-0.5))^2+c}$$と共通です)

☝(|x|+i(|y+0.5|-0.5))^2-0.3-1.68iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2+0.14-1.95iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-1.14-1.48iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-2.03iのジュリア集合

☝(|x|+i(|y+0.5|-0.5))^2-1.27-1.48iのジュリア集合

黒領域のあるジュリア集合です。

☝(|x|+i(|y+0.5|-0.5))^2+0.49-1.67iのジュリア集合(46周期)

☝(|x|+i(|y+0.5|-0.5))^2+0.57-1.78iのジュリア集合(56周期)

☝(|x|+i(|y+0.5|-0.5))^2-0.37-1.61iのジュリア集合(77周期)

☝(|x|+i(|y+0.5|-0.5))^2-0.7-1.32iのジュリア集合(80周期)

☝(|x|+i(|y+0.5|-0.5))^2-0.51-1.51iのジュリア集合(101周期)

いつものです。

2個セット

「バーニングシップフラクタルと仲間たち」の記事で紹介した図形が2つ並んだ形のマンデルブロ集合を探してみました。

※以下、$${Y=|y+0.5|-0.5}$$とします。

☝(x+iY)^2+cのマンデルブロ集合

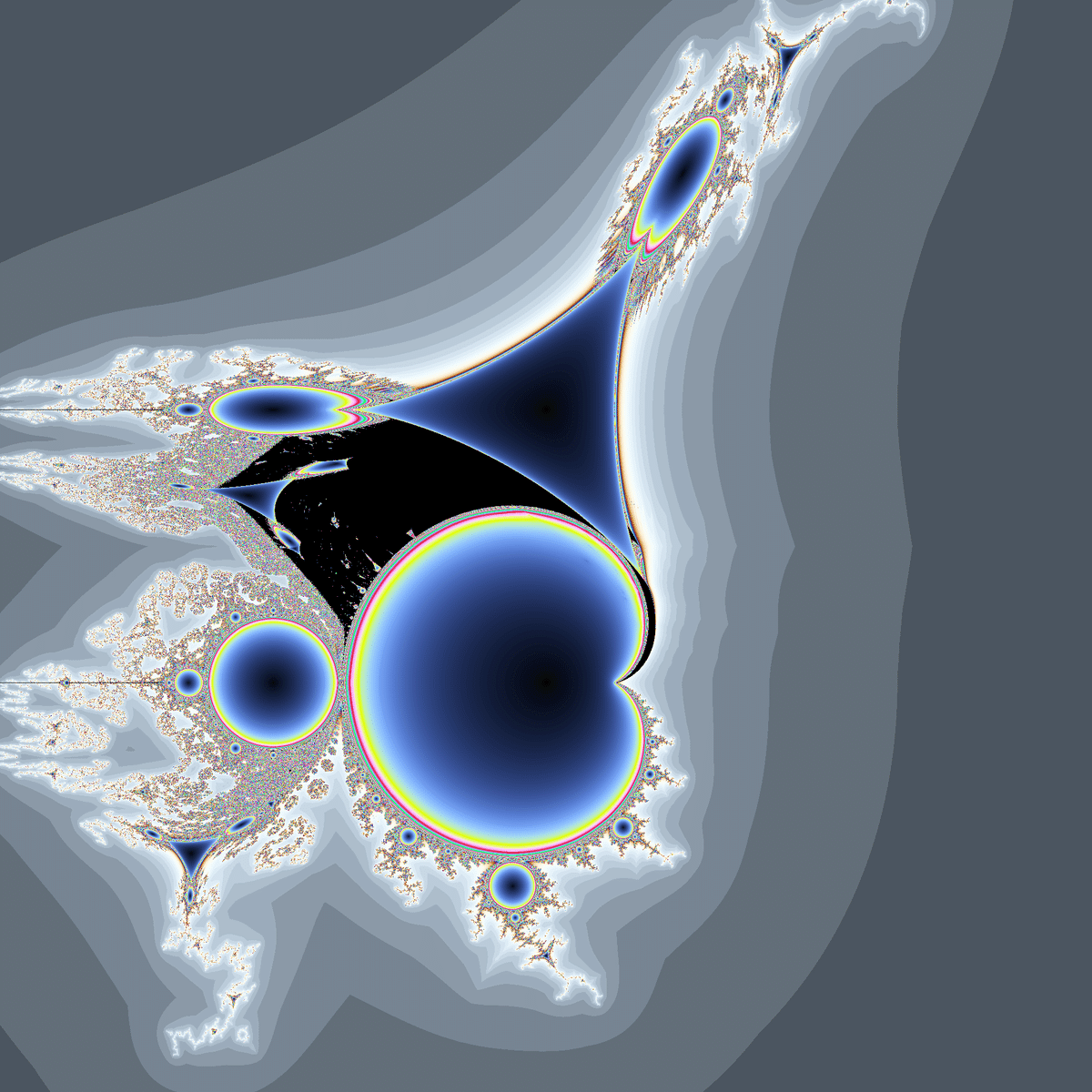
マンデルブロ集合とmandelbarです。

☝(|x|+iY)^2+cのマンデルブロ集合(再掲)

heart mandelbrotとperpendicular mandelbrotです。

☝(|x|+i|Y|)^2+cのマンデルブロ集合

バーニングシップフラクタル2個です。

☝(x+i|Y|)^2+cのマンデルブロ集合

perpendicular burning ship2個です。

☝(|x^2-Y^2|+a,2|xY|+b)のマンデルブロ集合

バッファローフラクタル2個です。

☝(|x^2-Y^2|+a,2x|Y|+b)のマンデルブロ集合

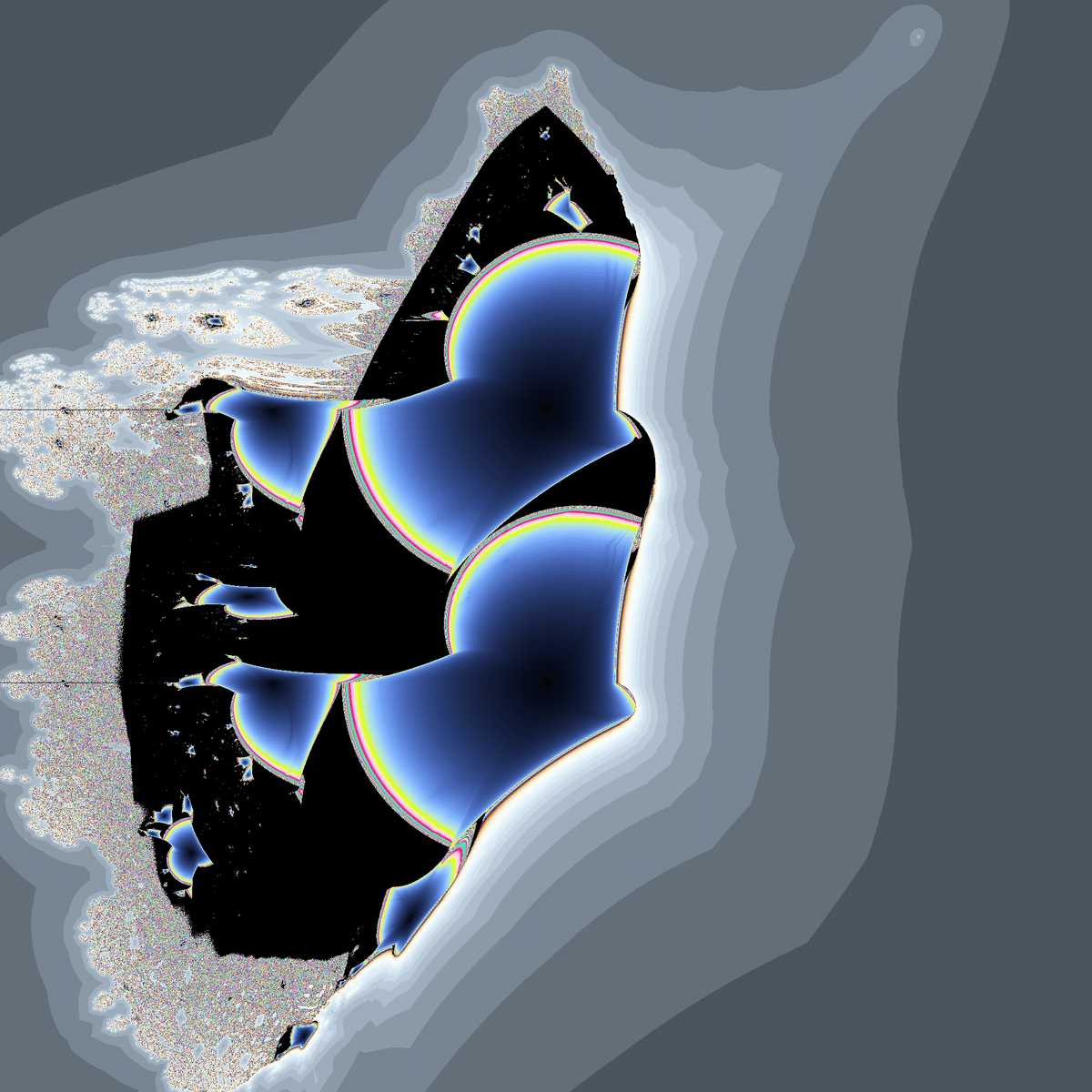
perpendicular buffalo2個です。

☝(|x^2-Y^2|+a,2x|Y|+b)のマンデルブロ集合

celtic mandelbrotとceltic mandelbarです。

☝(|x^2-Y^2|+a,2|x|Y+b)のマンデルブロ集合

celtic heartとperpendicular celticです。