
今週のフラクタル16 (c(z^4/4-z) 他)
どうも、108Hassiumです。
今回は$${c(\frac{z^4}{4}-z)}$$に関するフラクタル図形をお届けします。
c(z^4/4-z)

$${c(\frac{z^4}{4}-z)}$$の臨界点は1以外にも2つあるのですが、どれを使っても同じ見た目のマンデルブロ集合になるようでした。
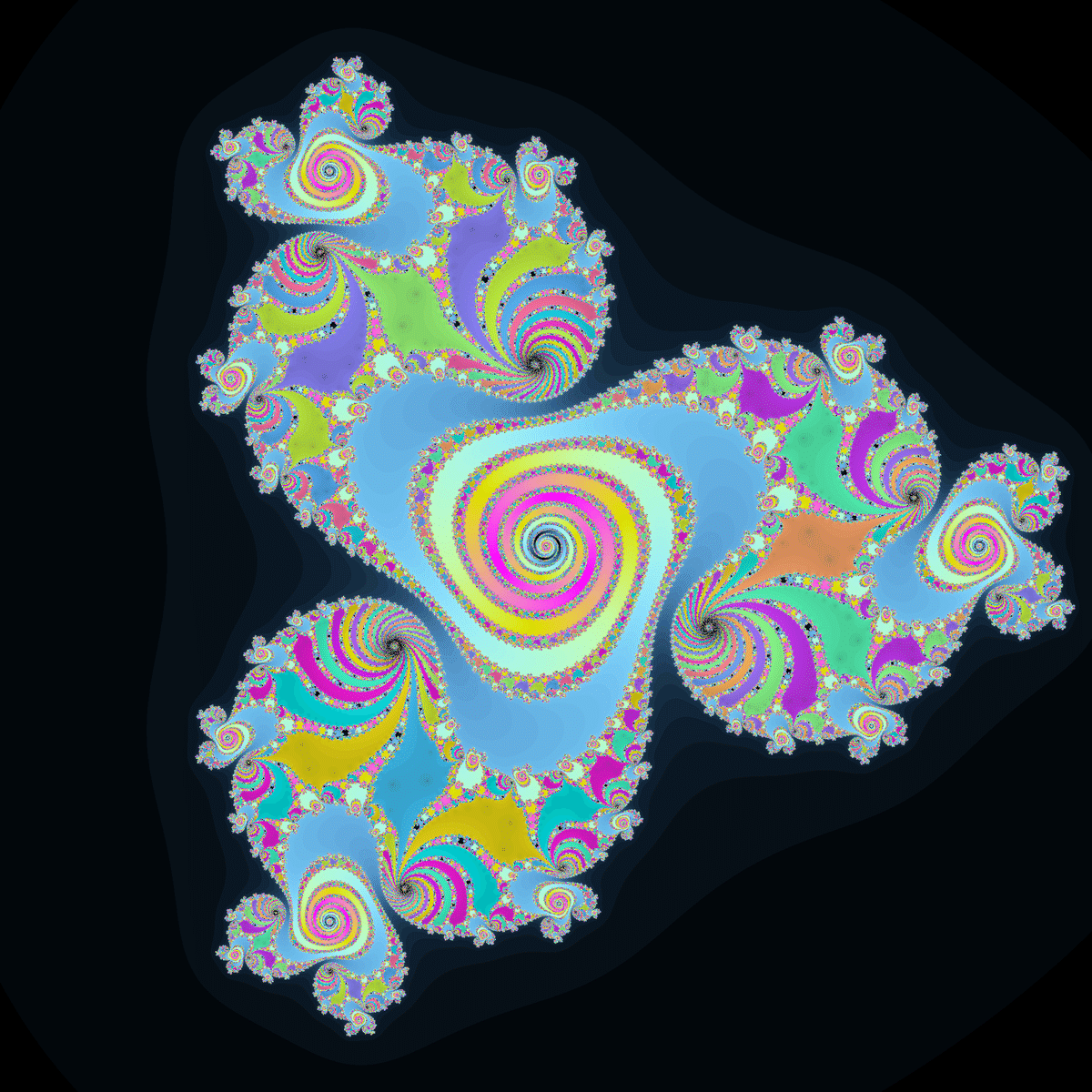


以前「$${c_1(c_2z^m-c_3z^n)}$$のジュリア集合は$${|m-n|}$$回回転対称」という経験則を紹介しましたが、$${c(\frac{z^4}{4}-z)}$$のジュリア集合もその法則通りに3回回転対称になるようです。
※☟$${c_1(c_2z^m-c_3z^n)}$$のジュリア集合の対称性の話をした記事
ところで、対称性の話をするだけなら$${c_1z^m+c_2z^n}$$としたほうが係数が1個少なくて済み、分かりやすさも損なわれないと思うのですが、あの記事を書いた当時の私は何故$${c_1(c_2z^m-c_3z^n)}$$なんて式を使ったんでしょうね。



前述の通り$${c(\frac{z^4}{4}-z)}$$には臨界点が3つありますが、それぞれの臨界点に対応する3つの吸引的サイクルが同時に存在することもあるようです。(先程のものは1種類のサイクルしか持たないものです)


先程の画像では3種類の収束領域が真ん中でつながるような形になっていましたが、もっと細かく混ざりあうような構造になることもあるようです。
なお、混ざる場合もそうでない場合も、よく見ると各種の収束領域の全体像は3つとも同じ形になっているようです。





いつものやつです。
c(con(z)^4/4-con(z))
※$${\text{con(z)}}$$は$${z}$$の複素共役

$${c(\frac{z^4}{4}-z)}$$と同じく、マンデルブロ集合も3回回転対称になるようです。

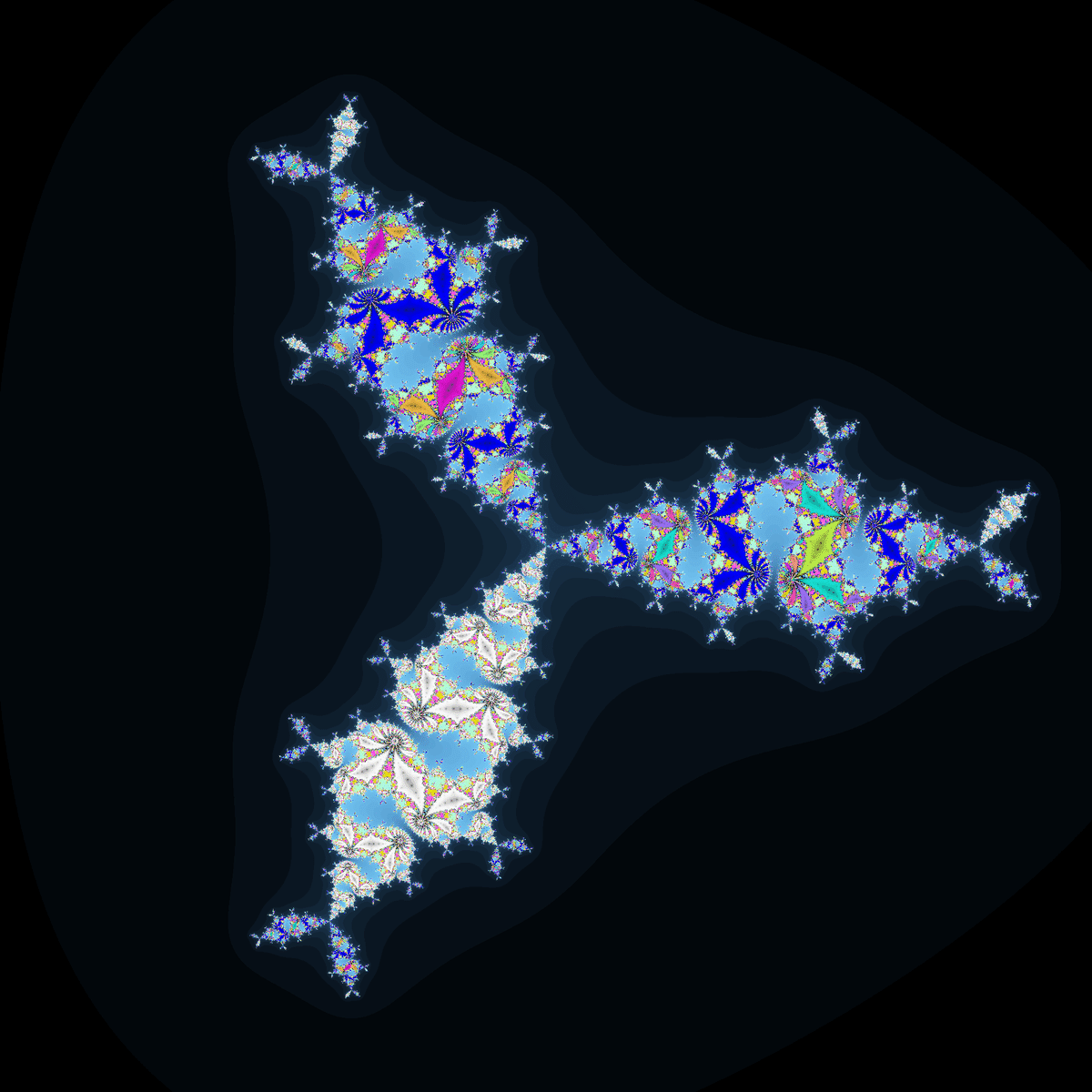
ジュリア集合も全体像は3回回転対称になるのですが、$${c(\frac{z^4}{4}-z)}$$とは違って各サイクルに対応する収束領域の形状が同じにならないようです。

以下の記事ではcon系関数のジュリア集合の特徴について解説していますが、それを踏まえてこのジュリア集合を見るとかなりヤバい形をしているのがわかると思います。


$${c}$$がマンデルブロ集合上の三角の領域の中にある場合、「サイクルの個数は1個か3個」という法則すら崩れるようです。

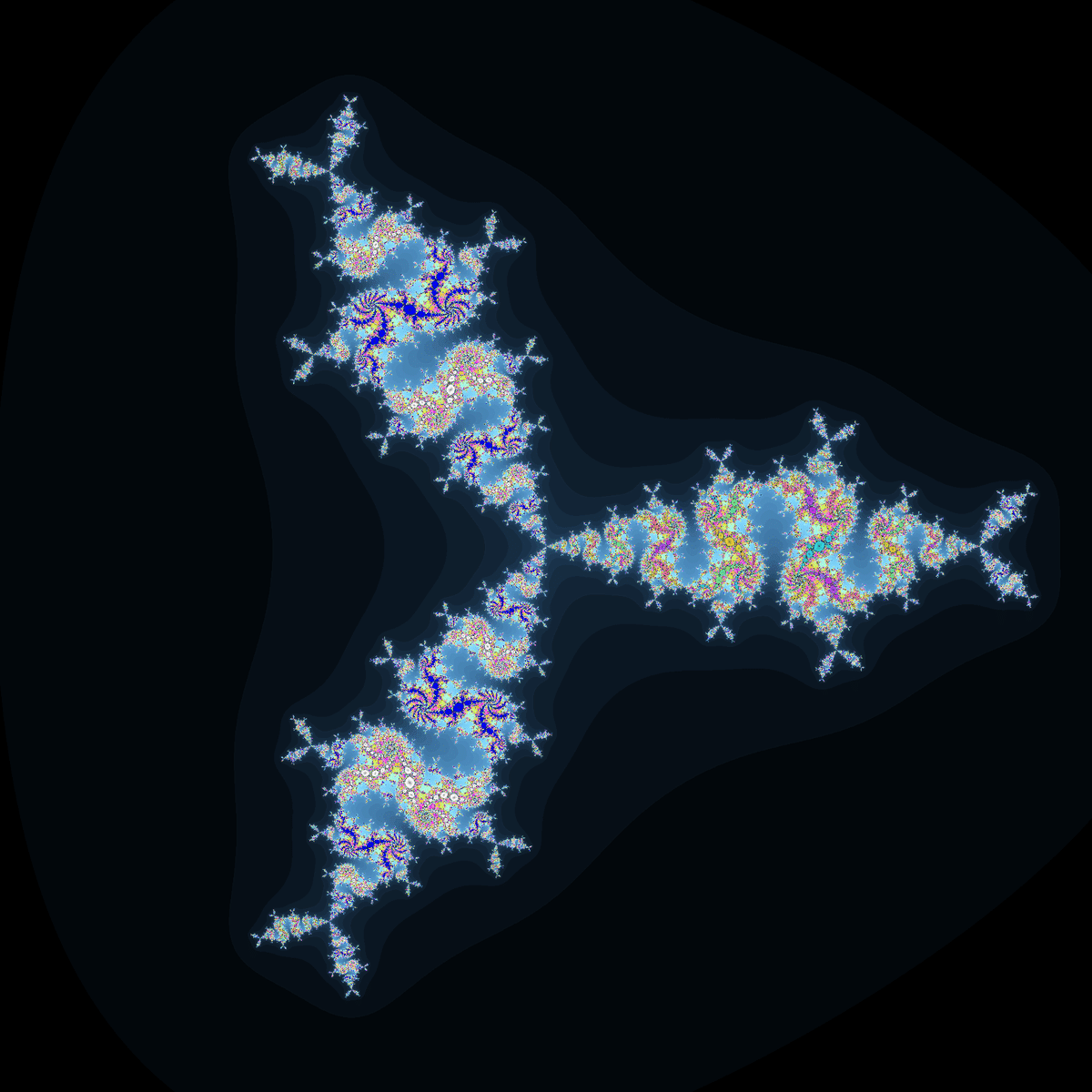

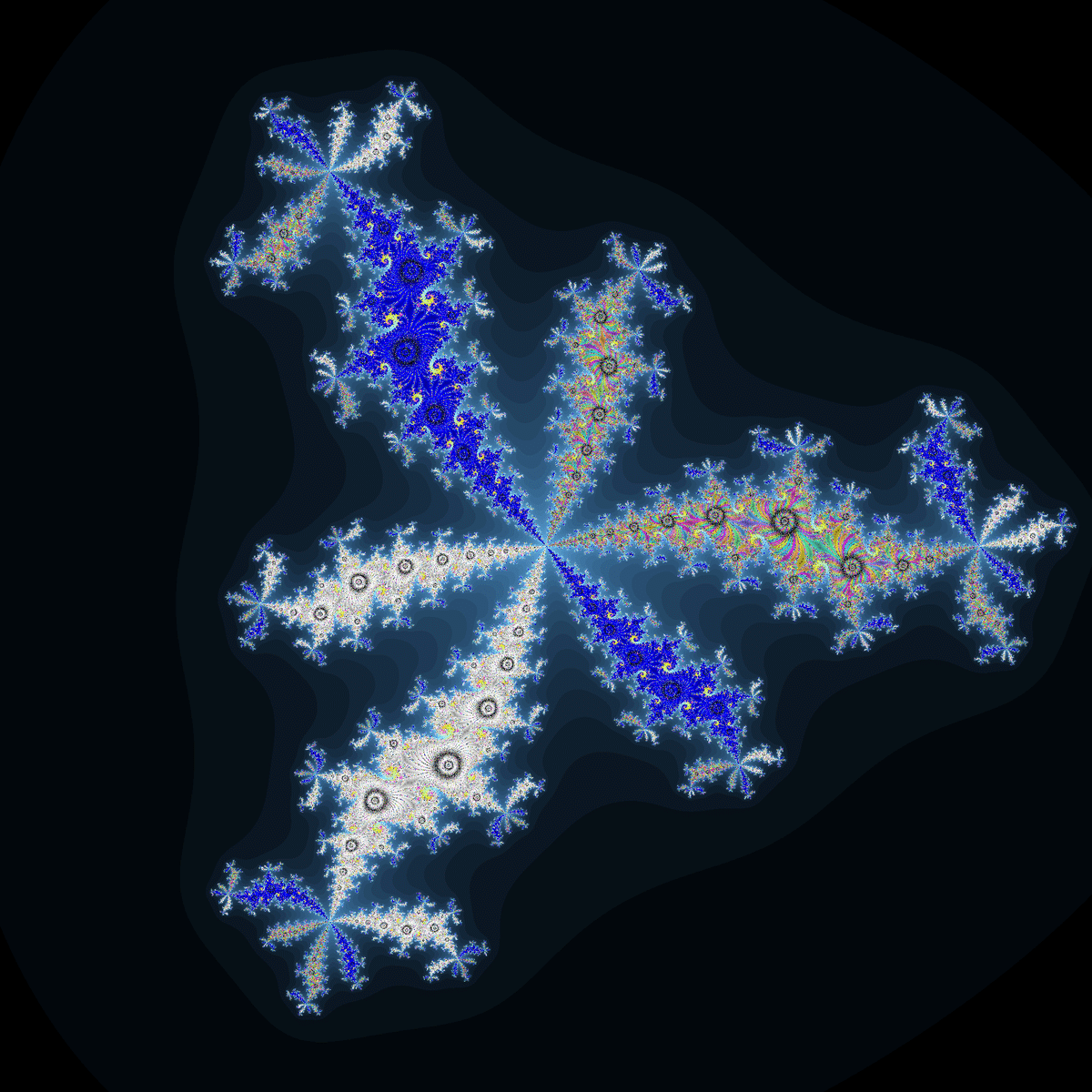

c(B(z)^4/4-B(z))
※$${B(x+iy)=|x|+i|y|}$$

これまでのものとは違い、3回回転対称にはならないようです。




ジュリア集合も3回回転対称にはならないようです。





