
今週のフラクタル38 ((z+0.03i)^6/(z^4+0.04z^3)+c)
どうも、108Hassiumです。
今回は$${\frac{(z+0.03i)^6}{z^4+0.04z^3}+c}$$に関するフラクタル図形をお届けします。
(z+0.03i)^6/(z^4+0.04z^3)+c
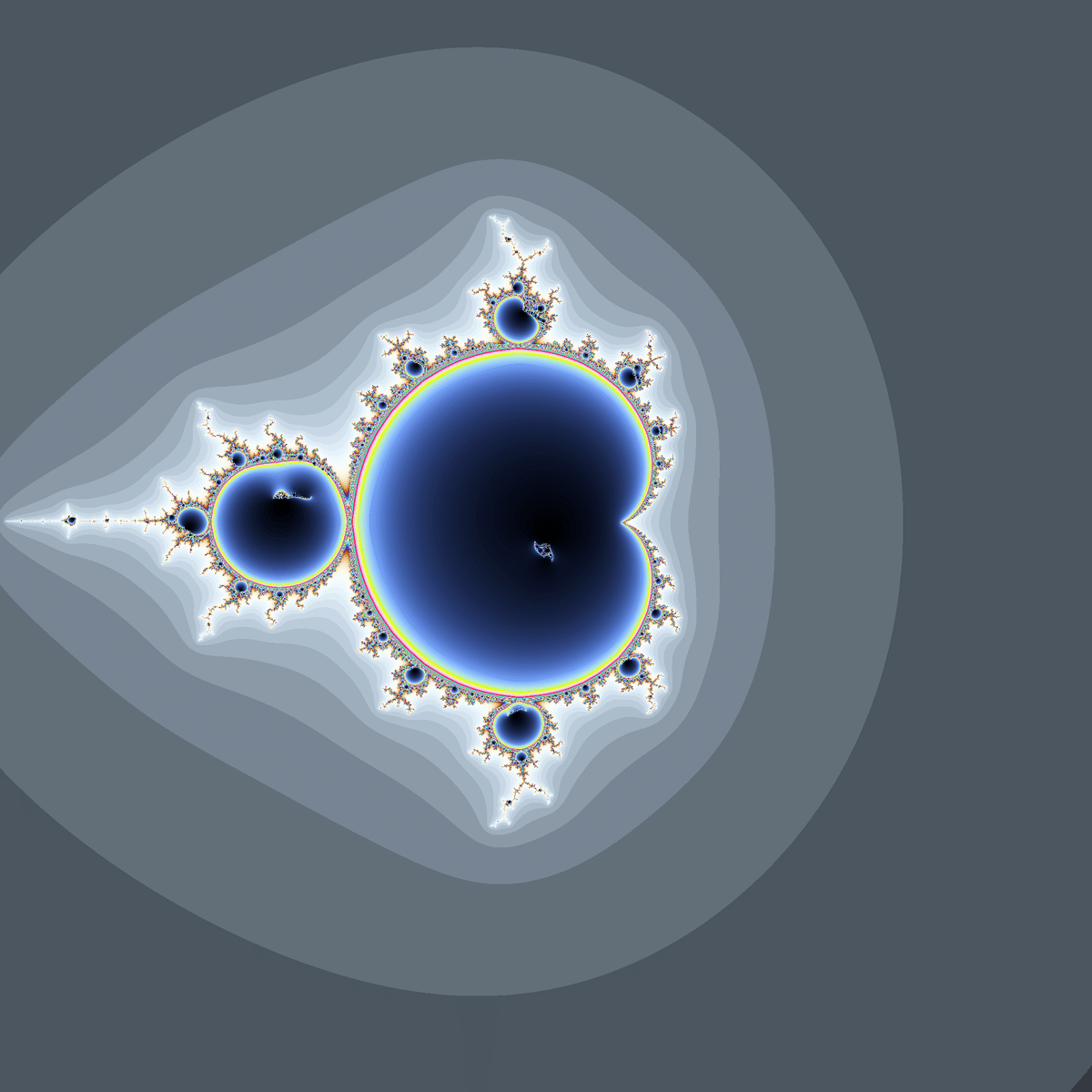

$${\frac{(z+0.03i)^6}{z^4+0.04z^3}+c}$$は$${z^2+c}$$を基にした摂動型関数なので、マンデルブロ集合の形状は$${z^2+c}$$のものを崩したような形になります。
臨界点は$${z=-0.03i,-0.03+0.03i}$$の2点で、多重度はそれぞれ5と2です。





$${z=-0.03i}$$の臨界点の多重度が5なのでジュリア集合は$${z^6+c}$$のジュリア集合のような形になると思ったのですが、収束領域内の模様に辛うじてそれっぽい特徴が出たり、飛び地型の場合に小さな六角形が出現する程度でした。
どうやら$${z^2+c}$$を基にした摂動関数では、多重度が大きすぎるとジュリア集合の形状に反映されにくくなるようです。






いかにも摂動系の関数っぽい奇抜な見た目のジュリア集合です。






環状に並んだ収束領域の中に白領域があるタイプのジュリア集合と、その派生パターンです。







花型の白領域のあるジュリア集合と、その派生パターンです。





以前の記事で「レアタイプ」として紹介した白領域の入り方をしたジュリア集合と、その派生パターンです。


よくわからない白領域の入り方をしたジュリア集合です。





いつものです。
(z^n+bz^(n-1))/(z+a)^m+c
以下の記事で、$${f(z)=\frac{z^n+bz^{n-1}}{(z+a)^m}+c}$$という形の関数の性質を紹介しました。
紹介した内容は、大体こんな感じでした。
$${a}$$と$${b}$$の絶対値が小さければ、$${f(z)}$$は$${z^{n-m}+c}$$に摂動を加えた関数と見做せる。
臨界点は$${z=0}$$を含む計3点で、多重度は$${z=0}$$が$${n-2}$$で他の2点は1。
$${m(n^2-mn-n+m)}$$が平方数なら、1重臨界点2個が1個の2重臨界点になるような有理数$${(a,b)}$$が存在する
要するに$${f(z)}$$は「$${z^{n-m}+c}$$を基にした摂動型関数で、臨界点が2個あって多重度が両方とも2以上」という関数が欲しくて考えた関数なのですが、最終的に「$${m(n^2-mn-n+m)}$$が平方数」という条件を上手く捌けなかった、というのが以前の結果でした。
これに関して、ちょっとだけ新しい発見があったので紹介したいと思います。
まず、$${m(n^2-mn-n+m)}$$という式は$${n=m+k}$$と置くと
$${m(n^2-mn-n+m)\\=m((m+k)^2-m(m+k)-(m+k)+m)\\=m(m^2+2km+k^2-m^2-km-m-k+m)\\=m(km+k^2-k)\\=km(k+m-1)}$$
・・・という風に短い式で表せることに気付きました。
以下、$${D(k,m)=km(k+m-1)}$$とします。
$${km(k+m-1)}$$を$${m}$$の2次関数として平方完成すると$${k\left(\left(m+\frac{k-1}{2}\right)^2-\frac{(k-1)^2}{4}\right)}$$になるので、$${D(k,m)=D(k,-k-m+1)}$$が成り立つことがわかります。
つまり$${D(k,m)}$$が平方数になれば$${D(k,-k-m+1)}$$も平方数になるのですが、$${k}$$と$${m}$$が両方とも正なら$${-k-m+1}$$は負の整数になってしまいます。
そして、$${k}$$、$${m}$$、$${D(k,m)}$$に負の数が含まれていても「$${z^{n-m}+c}$$を基にした(中略)両方とも2以上」という関数を見つけられることもある、というのが第2の発見です。
まず、$${m}$$と$${n}$$が両方負の場合、つまり$${m=-p}$$、$${n=-q}$$($${p}$$と$${q}$$は正)の場合、$${f(z)}$$は以下のように変形できます。
$${\frac{z^n+bz^{n-1}}{(z+a)^m}+c\\=\frac{z^{-q}+bz^{-q-1}}{(z+a)^{-p}}+c\\=\left(\frac{1}{z^q}+\frac{b}{z^{q+1}}\right)(z+a)^p+c\\=\frac{(z+a)^p(z+b)}{z^{q+1}}+c}$$
この場合の$${f(z)}$$は$${z=0}$$の代わりに$${z=-a}$$が多重度の大きい臨界点になりますが、その他の特徴は$${m}$$と$${n}$$が両方正の場合と同じです。
次に$${k}$$が負の場合ですが、この場合は$${\frac{1}{f(z)-c}+c}$$が目的の関数になります。
例えば今回紹介した$${\frac{(z+0.03i)^6}{z^4+0.04z^3}+c}$$という関数は、$${(m,n)=(6,4)}$$、つまり$${k=-2}$$のケースを利用した関数です。
$${k=-2}$$ということは$${f(z)}$$は「$${\frac{1}{z^2}+c}$$に摂動を加えた関数」になるのですが、逆数にして定数項の位置を直すことで$${z^2+c}$$型の関数が得られます。
また、$${(k,m)=(-2,6)}$$の場合は$${D(k,m)}$$も負になります。
この場合は$${a}$$と$${b}$$に関する条件に虚数が混ざってきますが、最終的に$${a}$$と$${b}$$を「実部も虚部も有理数であるような複素数」の範囲で求めるうえでは特に問題になりません。
