
今週のフラクタル4 (指数・三角関数)
どうも、108Hassiumです。
今回は、訳あって今まであまり触れてこなかった指数関数や三角関数に関するフラクタル図形を紹介したいと思います。
指数関数

この画像は$${z^2+c}$$のマンデルブロ集合などと同じようにEscape time algorithmで描画したもので、発散判定にはx*x+y*y>100という式を使用しています。
※☟Escape time algorithmの説明のある記事
収束領域をよく見ると発散領域に切り取られたような形になっており、本来収束するはずの部分が誤って発散判定になっていることが予想できます。


判定方法を変えることで切り取られていた部分が見えるようになりましたが、それでもまだ途切れている部分があるように見えます。

思い切って発散判定を無くしてみましたが、オーバーフローで正常に描画できない領域(白い部分)が生じてしまいました。

画像フォルダから発掘された、正体方法不明の画像です。
形状からして$${\text{exp}(z)+c}$$のマンデルブロ集合で間違いないと思うのですが、どういった条件で描画したのかわかりませんでした。





ジュリア集合でもマンデルブロ集合と同様に(発散判定の誤作動によって)ヤシの木のような模様が現れるようです。

$${z^2+c}$$のもののような普通(?)のマンデルブロ集合と、$${\text{exp}(z)+c}$$とも違う奇妙な特徴が混在するマンデルブロ集合です。
右側の縦線のそばには収束領域っぽい丸い形が見えますが、色的には発散領域っぽいです。

普通のジュリア集合です。

「収束領域っぽい発散領域」に対応するジュリア集合です。
マンデルブロ集合と同様に、こちらでも「収束領域っぽい発散領域」が現れました。

$${\text{exp}(x)-1}$$のニュートンフラクタルです。
※☟ニュートンフラクタルの説明
三角関数

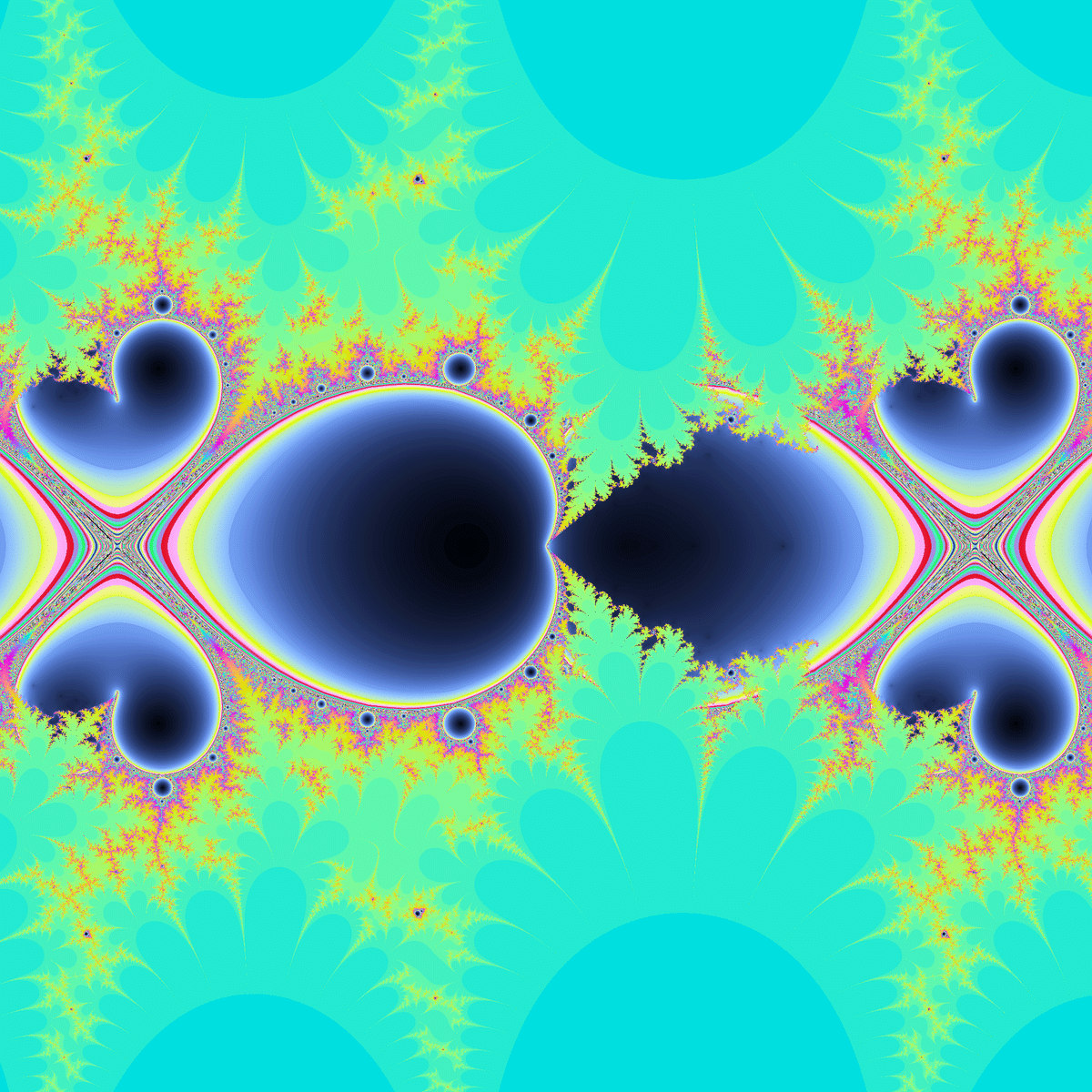




$${\text{sin}(z)+c}$$のマンデルブロ・ジュリア集合は、$${\text{exp}(z)+c}$$や$${\text{exp}(-z)+z+c}$$と比べると多項式関数などと近い見た目をしています。

$${y=\text{cos}(x)+c}$$のグラフは$${y=\text{sin}(x)+c}$$のグラフと同じ形ですが、マンデルブロ集合も同じ形になるようです。

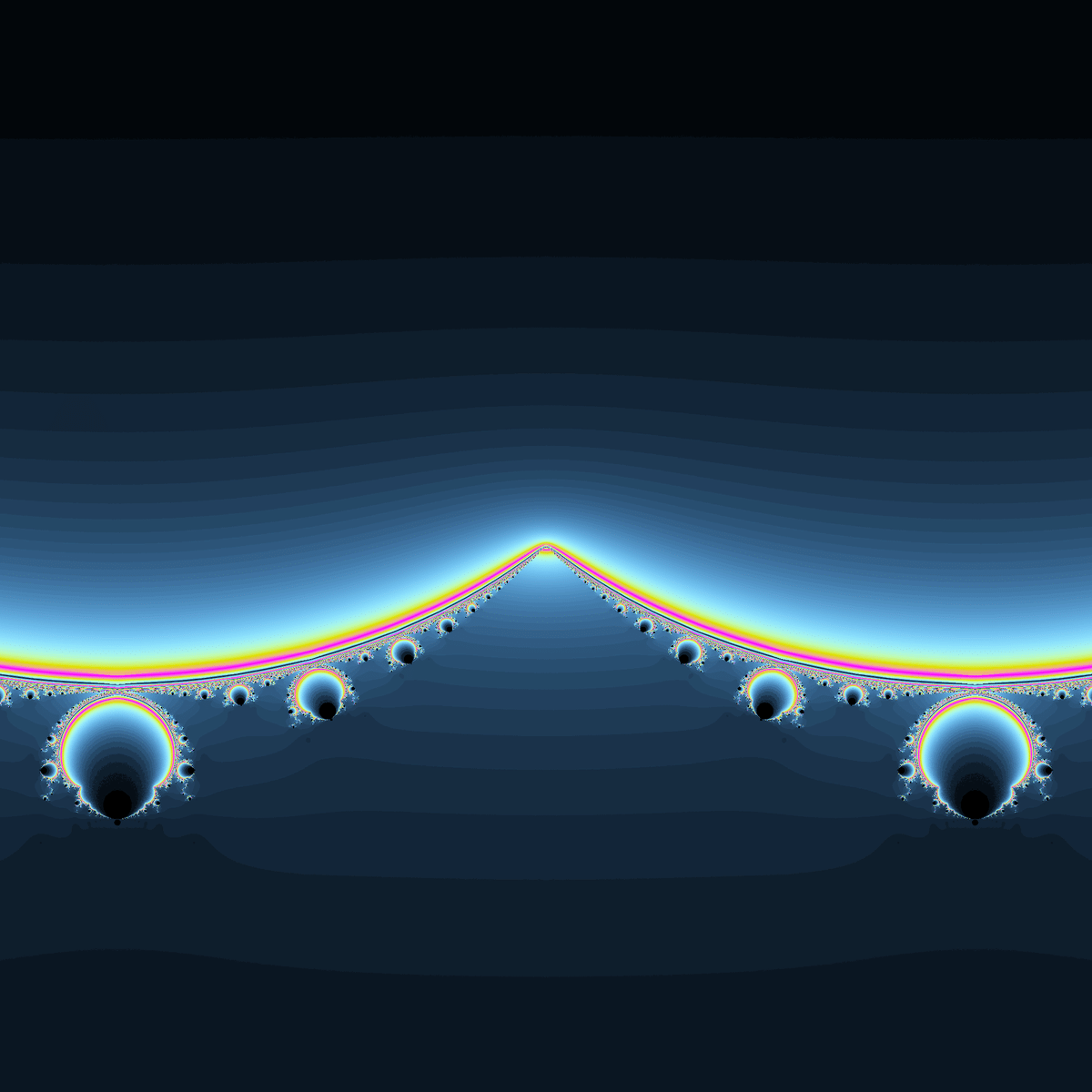


実軸上で発散しまくる$${\text{tan}(x)}$$ですが、マンデルブロ・ジュリア集合は意外にも発散領域を持たないようです。

$${\text{sin}(x)}$$のニュートンフラクタルです。
扱いにくい関数
Escape time algorithmでマンデルブロ集合やジュリア集合を描画する場合、関数の性質によって「扱いやすさ」が変わります。
初等関数(高校数学で出てくるような関数)で一番扱いやすいのは2次関数で、それ以外は以下のような順番で扱いにくくなっていきます。
3次以上の多項式関数:臨界点が複数個になる。
有理関数:特異点(極)が存在し、発散領域を持たない関数($${z-\frac{z^3-1}{3z^2}}$$など)が現れる。
指数・三角関数:極よりも質の悪い特異点(真性特異点)が存在し、発散判定が機能しなくなることがある。
$${f(z)=\text{exp}(z)+c}$$の場合は無限遠点が真性特異点になっているようで、$${|z|}$$が大きくなっても$${|f(z)|}$$がさらに大きい値になるかどうかはわからなくなっています。
実際、$${\text{exp}(x+iy)}$$の実部は$${\text{exp}(x)\text{cos}(y)}$$なので、$${x}$$が大きくても$${\text{cos}(y)}$$が小さければ$${\text{exp}(x+iy)}$$の実部は小さな値になります。
このような性質により、指数・三角関数のマンデルブロ集合やジュリア集合は発散判定がうまくいかず正確に描画できないようです。
ちなみにこれまでの記事で指数・三角関数系のフラクタル図形をあまり扱ってこなかったのは、上記の理由のほかにも「Processingのexp、sin、cos等の関数はdouble型の変数を扱えない」というのもあります。
さて、こんなにも扱い辛い指数・三角関数ですが、これよりもさらに扱いにくい関数のグループがあります。
4.対数関数:値が一意に定まらず、適当に選ぶと関数が不連続になる。
例えば任意の整数$${n}$$について$${\text{exp}((2n+1)i\pi)=-1}$$が成り立つので、$${\text{log}(-1)}$$の値には無限個の候補が存在することになります。
そして、$${c^z}$$や$${z^z}$$のような「複素数の複素数乗」を計算するには対数関数を使う必要があり、さらに平方根や逆三角関数も同様の問題を抱えています。
こういった関数でフラクタル図形を描画しようとすると、不連続性の影響により不自然に途切れた形になってしまったり、数値の選び方によって違うフラクタル図形になってしまったりします。

