
バーニングシップフラクタルと仲間たち
どうも、108Hassiumです。
以前、Youtubeでこんな動画を発見しました。
何らかのフラクタル図形を拡大して美しい模様が現れる様を映した動画ですが、この手の動画でよく使われるマンデルブロ集合とは明らかに違う図形です。
タイトルには「burning ship」とありますが、どうやらバーニングシップフラクタルとも違うようです。
※「マンデルブロ集合」と「バーニングシップフラクタル」を知らない方は以下の記事を読むといいかと思います。
そこで「perpendicular burning ship」でググってみたところ、以下のページに辿り着きました。
どうやら、バーニングシップフラクタルのような「マンデルブロ集合の計算式に絶対値関数を混ぜてできるフラクタル図形」の名前を12個まとめた画像のようです。
というわけでこの記事では、この画像に載っている12個の図形や関連するフラクタル図形を紹介したいと思います。(私用の備忘録も兼ねています)
Mandelbrot
先程のリンク先の画像に合わせて、まずはマンデルブロ集合について少し説明します。

マンデルブロ集合は、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=x_n^2-y_n^2+a\\y_{n+1}=2x_ny_n+b\end{cases}}$$
※今回の記事では複素数を使わずに説明します。また、特に断らない限り数列の初期値は0とします。
$${(a,b)}$$がマンデルブロ集合に含まれるとき$${x_n}$$と$${y_n}$$は大抵の場合周期数列へと近づいていくので、周期数列に収束するスピードでマンデルブロ集合の内側を彩色すると以下のようになります。
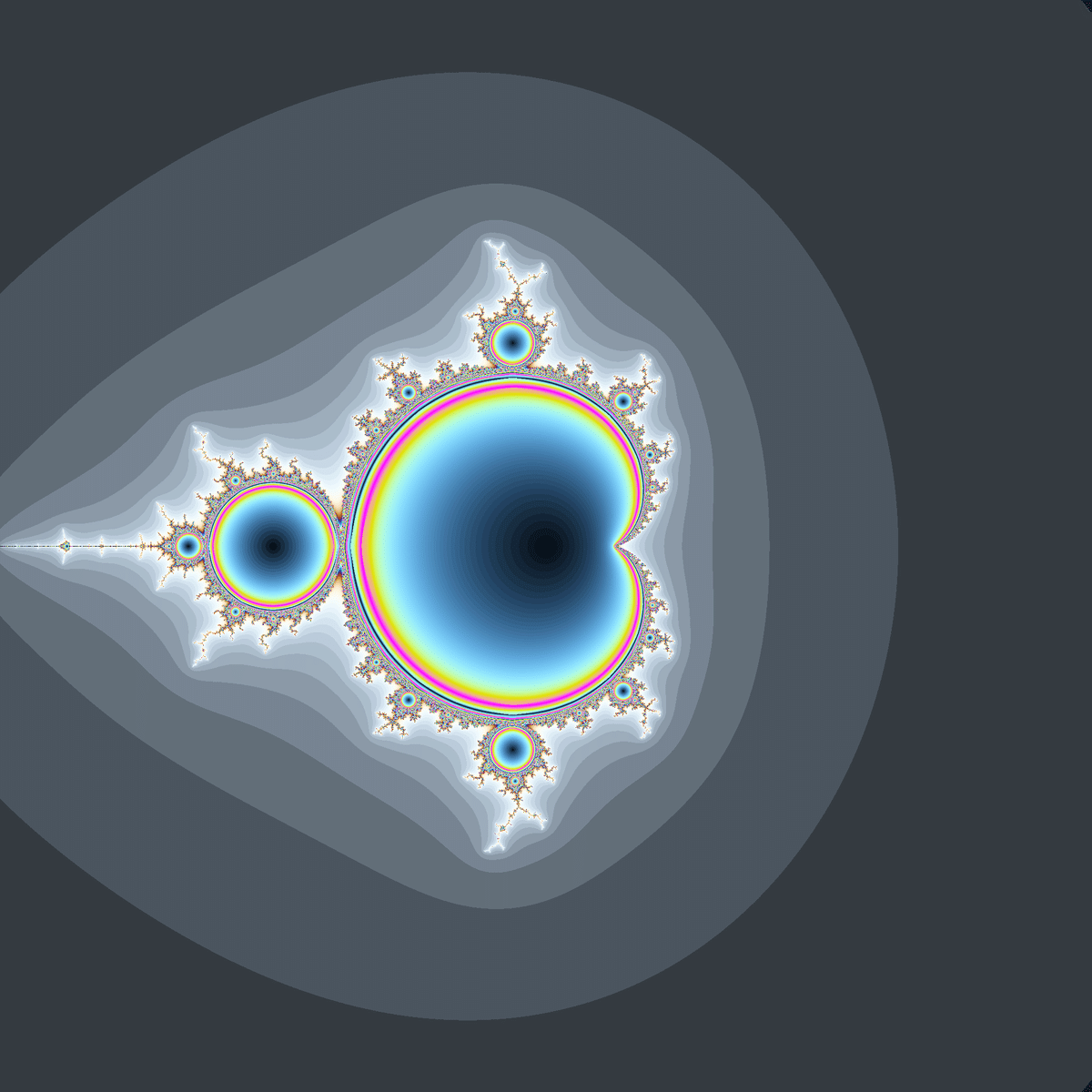
マンデルブロ集合の細部を拡大すると、以下のようにマンデルブロ集合を縮小させたような形が見られます。

※この記事では、座標平面の$${y}$$軸の向きを「下が+」とします。なので(-0.1,1)という点は、マンデルブロ集合の全体図では下半分の領域に位置する点を表します。
また、この記事では以下のような形の数列が無限大に発散しないような初期値(実数)の2つ組$${(x_0,y_0)}$$全体からなる集合を「$${(f(x,y),g(x,y))}$$のジュリア集合」と呼ぶことにします。
$${\begin{cases}x_{n+1}=f(x_n,y_n)\\y_{n+1}=g(x_n,y_n)\end{cases}}$$
例えば$${(x^2-y^2+0.3,2xy+0.5)}$$のジュリア集合は以下のようになります。

中央付近から広がるカラフルな領域がジュリア集合で、先程のマンデルブロ集合と同じく周期数列への収束速度で彩色してあります。
以上の説明は私のnoteの記事をよく読むという人なら大体知っていることかと思いますが、この記事ではバーニングシップフラクタルとその仲間たちに対しても同様に内部の彩色・細部の拡大・ジュリア集合化などをするとどうなるのか、といったことを見ていきたいと思います。
Burning ship
バーニングシップフラクタルは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=x_n^2-y_n^2+a\\y_{n+1}=2|x_ny_n|+b\end{cases}}$$
wikipediaなどで使われている式と見た目は違いますが、意味的には一緒です。

なお、「Mandelbrot ABS Variations Complete Set of Formulas」に載っている式は以下の通りで、描画すると上下さかさまの画像が出来上がります。
$${\begin{cases}x_{n+1}=x_n^2-y_n^2+a\\y_{n+1}=-2|x_ny_n|+b\end{cases}}$$
おそらく「Mandelbrot ABS (略)」の式は、$${y}$$軸の向きを「上が+」に直した状態で船っぽく見える向きになるようにしてあるのだと思います。(以下、y軸の向きは下向きを+とし、それに合わせて修正した計算式を載せることにします)
さて、収束速度による内部彩色を行うと以下のようになります。
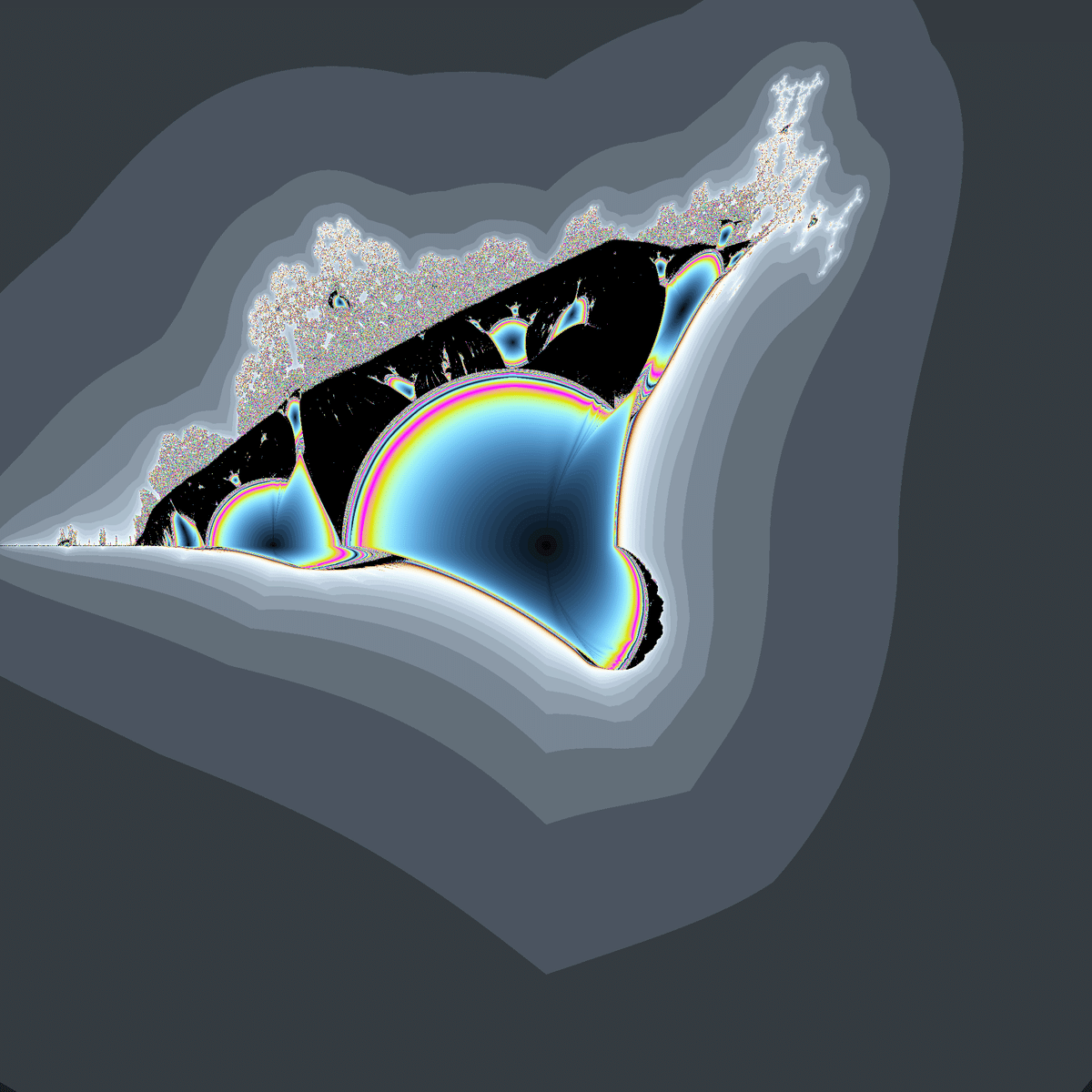
真っ黒いままの領域は、$${x_n}$$と$${y_n}$$が周期数列に収束していかずカオス的な挙動をとる領域です。
拡大図はこんな感じです。

左端の方を拡大すると、本体よりも船っぽい形がたくさん並んでいます。


しかし、別の場所をよく見てみるとバーニングシップフラクタル本体とは違った図形が見られ、これらは後述の「celtic mandelbar」と「celtic mandelbrot」に似ています。







$${(x^2-y^2+a,2|xy|+b)}$$のジュリア集合は、$${(x^2-y^2+a,2xy+b)}$$のものと比べると全体的なシルエットの面白さでは劣るものの内側に美しい模様が現れるのが特徴的です。
また、$${x}$$軸と$${y}$$軸の両方について常に線対称な形になるようです。

$${x_n}$$と$${y_n}$$は、発散しなければ周期数列に収束するかしないかのどちらかだけになることが多いですが、ごく一部の$${(a,b)}$$の組み合わせでは周期数列に収束する初期値と収束しない初期値が混在するようです。
Mandelbar
mandelbarは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=x_n^2-y_n^2+a\\y_{n+1}=-2x_ny_n+b\end{cases}}$$
※以降の図形の名称は、基本的に英語名のままでいきます。


マンデルブロ集合と同じく、カオス軌道に収束する真っ黒な領域を持たないのが特徴です。


拡大するとマンデルブロ集合とmandelbarの両方に似た収束領域が現れますが、どちらも押しつぶされたような形になっています。
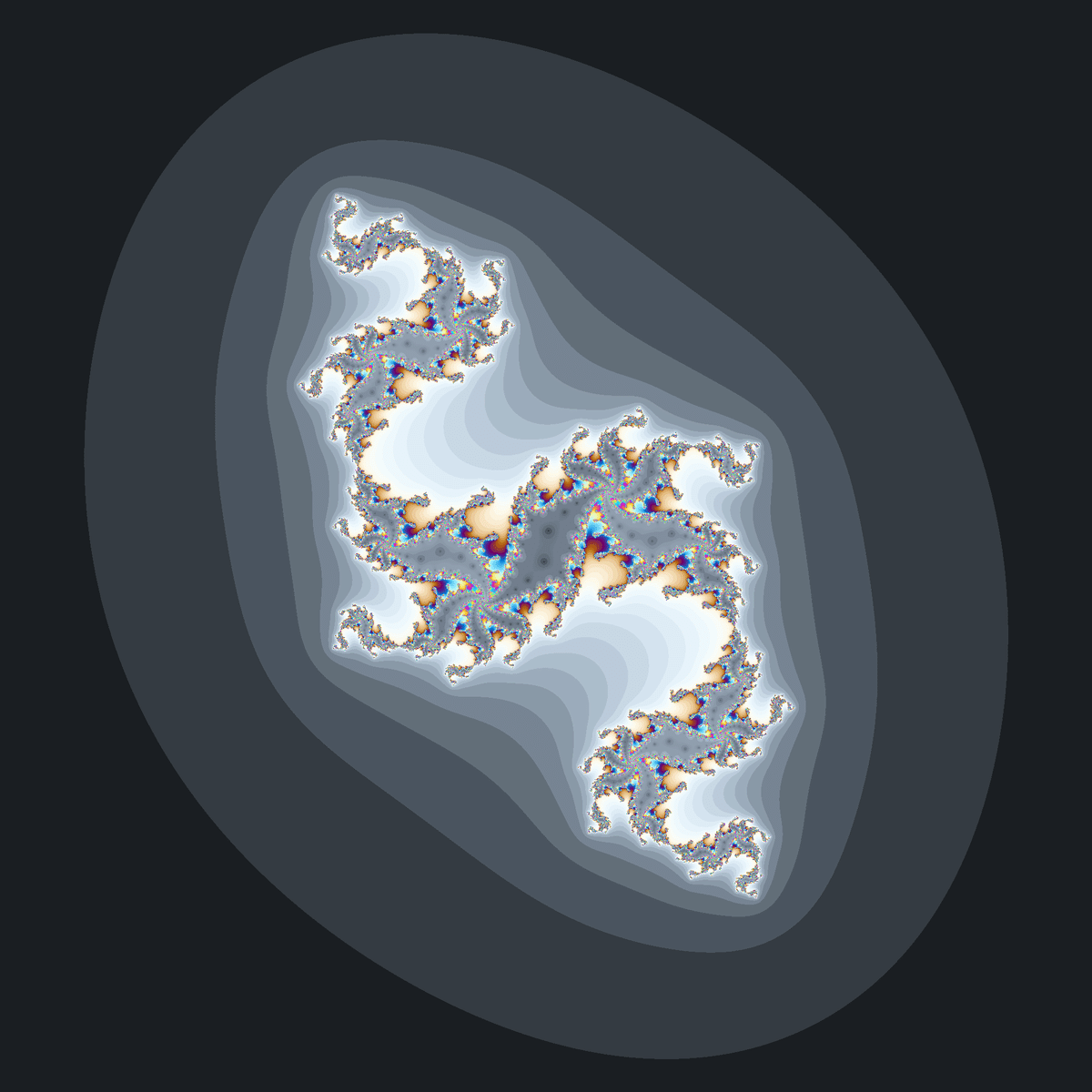
ジュリア集合の形は、$${(x^2-y^2+a,2xy+b)}$$のものと似たような形になっています。
$${(x^2-y^2+a,-2xy+b)}$$のジュリア集合の形状については、以下の記事でもう少し詳しく分析しているので興味がある方は読んでみてください。
Perpendicular mandelbrot
perpendicular mandelbrotは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=x_n^2-y_n^2+a\\y_{n+1}=-2|x_n|y_n+b\end{cases}}$$


perpendicularは「垂直」という意味で、「マンデルブロ集合を3次元に拡張したものの一つにおいて、2Dマンデルブロ集合と垂直な断面としてこの図形が現れる」というのが名前の由来であるという話をどこかで読んだ気がするのですが、残念ながら見つけられませんでした。
ちなみに私は以前「マンデルブロ集合を4次元に拡張したもの」に関する記事を書いたのですが、残念ながら私が扱ったものにはperpendicular mandelbrotは現れませんでした。



拡大すると小さいperpendicular mandelbrotのほか、後述のheart mandelbrotやperpendicular burning shipっぽい形が見られます。




ジュリア集合は、$${y}$$軸について線対称になるようです。
Perpendicular burning ship
perpendicular burning shipは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=x_n^2-y_n^2+a\\y_{n+1}=2x_n|y_n|+b\end{cases}}$$
※先述の通り、$${y}$$軸の向きに合わせて定義式を変えてあります。


右下の部分がマンデルブロ集合と同じようにワサワサしているのが特徴的です。

perpendicular buning shipのほか、perpendicular mandelbrotと似た形が見られます。







ジュリア集合は$${x}$$軸について線対称になるようです。
Buffalo
バッファローフラクタル(仮称)は、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=|x_n^2-y_n^2|+a\\y_{n+1}=2|x_ny_n|+b\end{cases}}$$
※先述の通り、$${y}$$軸の向きに合わせて定義式を変えてあります。




拡大するとバッファローフラクタルっぽい形が見えますが、それ以外にも何だかよくわからない(今回紹介するフラクタル図形のどれとも似ていない)収束領域もあります。









ジュリア集合は、線対称かつ4回回転対称という非常に高い対称性を持つようです。
Perpendicular buffalo
perpendicular buffaloは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=|x_n^2-y_n^2|+a\\y_{n+1}=2x_n|y_n|+b\end{cases}}$$
※先述の通り、$${y}$$軸の向きに合わせて定義式を変えてあります。





拡大すると小さいperpendicular buffaloのほか、後で出てくるperpendicular celticやよくわからない形が見られます。










ジュリア集合は$${x}$$軸について線対称ですが、左上と左下の領域をよく見ると部分的に斜めに線対称になっているように見えます。
Heart mandelbrot
heart mandelbrotは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=x_n^2-y_n^2+a\\y_{n+1}=2|x_n|y_n+b\end{cases}}$$


凹凸が少なく、フラクタル図形としてはあまり面白くない形をしています。


拡大するとheart mandelbrotのほかにバーニングシップフラクタルっぽい形が見つかりました。



ジュリア集合は$${y}$$軸について線対称ですが、左上と右上の領域をよく見ると部分的に斜めに線対称になっているように見えます。
また、今までのものと違い「周期数列に収束する初期値とそうでない初期値が混在するパラメータ」は見つけられませんでした。
Celtic mandelbrot
celtic mandelbrotは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=|x_n^2-y_n^2|+a\\y_{n+1}=2x_ny_n+b\end{cases}}$$


celticという単語は「ケルト語の」「ケルト族の」等の意味を持ちますが、このフラクタル図形との関係はよくわかりませんでした。

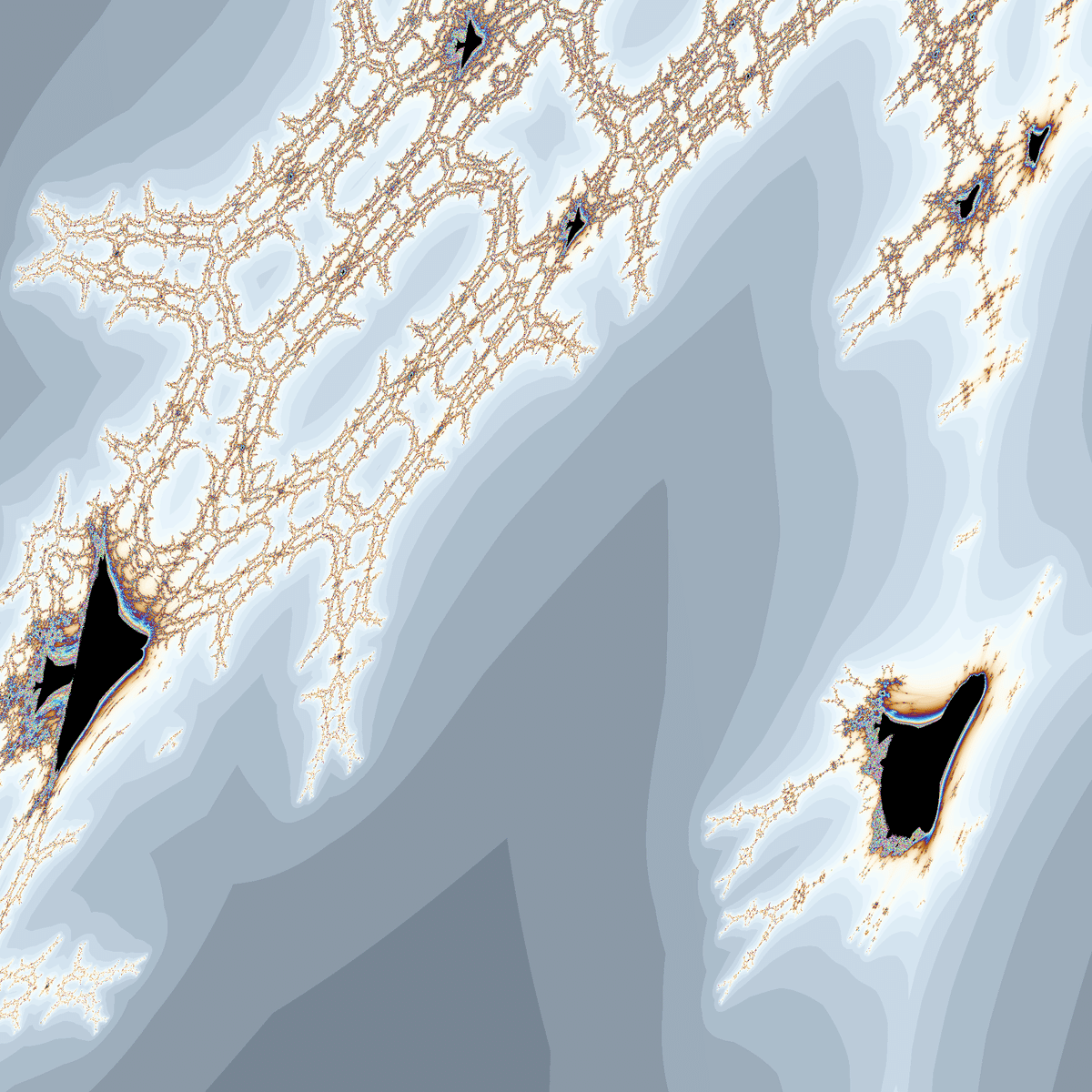
拡大するとceltic mandelbroのほかによくわからない形が見られます。





ジュリア集合は直線$${y=\pm x}$$について線対称になるようです。
Celtic mandelbar
celtic mandelbarは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=|x_n^2-y_n^2|+a\\y_{n+1}=-2x_ny_n+b\end{cases}}$$



拡大するとcelticmandelbarやceltic mandelbrotに似た形のほか、よくわからない領域が見られました。






ジュリア集合は、celtic mandelbrotと同様に直線$${y=\pm x}$$について線対称になるようです。
Celtic heart
celtic heartは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=|x_n^2-y_n^2|+a\\y_{n+1}=2|x_n|y_n+b\end{cases}}$$



拡大すると小さいceltic heartが見られるのですが、それ以外の図形に似た収束領域は見つけられませんでした。





ジュリア集合の対称性は、heart mandelbrotと同じく$${y}$$軸について線対称になるようです。(左上と右上が斜めに線対称になっているように見えること、周期軌道とカオス軌道が混在するパラメータが見つからなかったことも共通しています)
Perpendicular celtic
perpendicular celticは、以下の数列が無限大に発散しないような実数の2つ組$${(a,b)}$$全体からなる集合です。
$${\begin{cases}x_{n+1}=|x_n^2-y_n^2|+a\\y_{n+1}=-2|x_n|y_n+b\end{cases}}$$




拡大するとpependicular celticやよくわからない形が見られます。









ジュリア集合の対称性は、heart mandelbrotやceltic heartと同じく$${y}$$軸について線対称になるようです。
