
今週のフラクタル12 (con(z)^3/(con(z)+0.1i)+c)
どうも、この間「今週のフラクタル」シリーズの投稿間隔がほぼ月1になっていて実質「今月のフラクタル」と化していることに気付いた108Hassiumです。
今週は$${\frac{\text{con}(z)^3}{\text{con}(z)+0.1i}+c}$$($${\text{con}(z)}$$は$${z}$$の複素共役)に関するフラクタル図形をお届けします。
con(z)^3/(con(z)+0.1i)+c

$${\frac{\text{con}(z)^3}{\text{con}(z)+0.1i}+c}$$のマンデルブロ集合は$${\text{con}(z)^2+c}$$のマンデルブロ集合の細部を崩したような形をしていますが、このことは「$${\frac{z^3}{z+0.1i}+c}$$のマンデルブロ集合は$${z^2+c}$$のマンデルブロ集合の細部を崩したような形をしている」という事を踏まえるととても自然な性質であるように感じます。
※☟$${\text{con}(z)^2+c}$$の解説のある記事
※☟$${\frac{z^3}{z+0.1i}+c}$$の解説のある記事

中央付近にある穴の拡大図です。
穴の中をよく見ると、$${c(\text{con}(z)+\frac{1}{\text{con}(z)})}$$や$${\frac{c}{\text{con}(z)^2-1}+1}$$のような「有理関数の$${z}$$を$${\text{con}(z)}$$に置き換えた関数」特有の真っ黒い領域が現れています。
※☟真っ黒い領域の解説のある記事




(広義の)摂動ジュリア集合でよく見る感じの、奇抜な形をしたジュリア集合です。
S字型の構造とZ字型の構造が向かい合うように出現するという$${\text{con}}$$系のジュリア集合の特徴も併せ持っています。



マンデルブロ集合の中央付近にあった穴の中の値に対応するジュリア集合です。
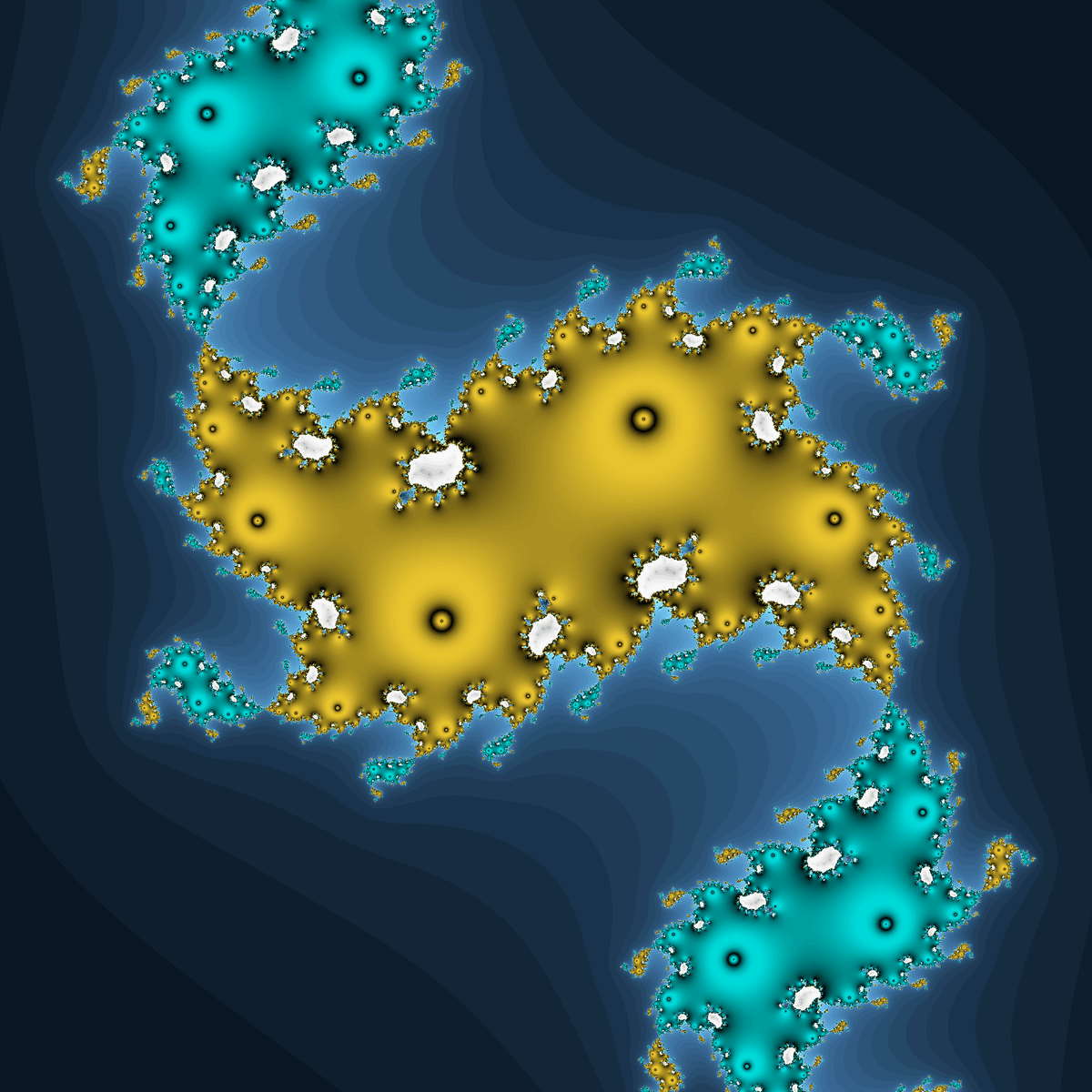








2種類の吸引的サイクルが存在するジュリア集合です。





いつものやつです。

無限周期と思しきジュリア集合です。
