
摂動系関数を作ろう
どうも、108Hassiumです。
「今週のフラクタル」シリーズでは、フラクタル図形を生成する関数としてこれまでに何度も「摂動系関数」というグループの関数を取り上げてきました。(正確な呼称や名称の定義は曖昧です)
今回の記事では、摂動系関数を作る方法を3つ紹介します。
※摂動系関数の大まかな説明は以下の記事をに書いてあります。
f+ε法
f+ε法は、「摂動」という言葉通り(?)に元の関数$${f(z)}$$に微小な変化(摂動項)を加える方法です。
例として、$${f(z)=\frac{1}{3}z^3-\frac{1}{2}z^2+c}$$に対して$${\varepsilon=\frac{a}{z}}$$という形の摂動項を加えた関数を考えます。
$${g(z)=f(z)+\varepsilon}$$を微分し、臨界点がシンプルな値になるような$${a}$$の値を求められるか試してみます。
$${g'(z)=z^2-z-\frac{a}{z^2}=0}$$
$${z^4-z^3-a=0}$$
$${z}$$についての4次方程式になってしまいました。
とりあえず解の1つを$${b}$$と置き、残りの3つの解を求められないか試してみます。
$${a=b^4-b^3}$$
$${z^4-z^3-b^4+b^3\\=(z-b)(z^3+bz^2+b^2z+b^3)-(z-b)(z^2+bz+b^2)\\=(z-b)(z^3+(b-1)z^2+(b^2-b)z+b^3-b^2)=0}$$
$${z^3+(b-1)z^2+(b^2-b)z+b^3-b^2\\=z^3-b^3+bz^2+b^2z-z^2-b^2-bz=0}$$
$${z}$$と$${b}$$についての対称式になったので、$${z+b}$$と$${bz}$$の式になるように変形します。
$${z^3-b^3+bz^2+b^2z-z^2-b^2-bz\\=(z+b)^3-3bz^2-3b^2z+bz^2+b^2z-(z+b)^2+2bz-bz\\=(z+b)^3-(z+b)^2-2bz(z+b)+bz=0}$$
$${bz}$$についての1次式になったので、$${bz}$$について解きます。
$${bz=\frac{(z+b)^3-(z+b)^2}{2(z+b)-1}}$$
ここで$${z+b=d}$$と置くと$${bz=\frac{d^3-d^2}{2d-1}}$$となることがわかるので、これを連立方程式として解きます。
$${\begin{cases}z+b=d\\bz=\frac{d^3-d^2}{2d-1}\end{cases}}$$
$${b=-z+d}$$
$${-z^2+dz=\frac{d^3-d^2}{2d-1}}$$
$${z^2-dz+\frac{d^3-d^2}{2d-1}=0}$$
$${z=\frac{1}{2}\left(d\pm\sqrt{d^2-\frac{4d^3-4d^2}{2d-1}}\right)\\=\frac{1}{2}\left(d\pm d\sqrt{1-\frac{4d-4}{2d-1}}\right)\\=\frac{1}{2}\left(d\pm d\sqrt{\frac{-2d+3}{2d-1}}\right)\\=\frac{1}{2}\left(d\pm\frac{d\sqrt{(-2d+3)(2d-1)}}{2d-1}\right)}$$
$${b=-\frac{1}{2}\left(d\pm\frac{d\sqrt{(-2d+3)(2d-1)}}{2d-1}\right)+d\\=\frac{1}{2}\left(d\mp\frac{d\sqrt{(-2d+3)(2d-1)}}{2d-1}\right)}$$
根号の中が有理式の2乗になれば$${b}$$も$${z}$$も有理式になるので、いつものアレをやります。
結果として、$${d=\frac{h^2-2h+4}{h^2+4}}$$と置くと$${(-2d+3)(2d-1)}$$は
$${\frac{-2h^2+4h-8+3h^2+12}{h^2+4}×\frac{2h^2-4h+8-h^2-4}{h^2+4}\\=\frac{(h^2+4h+4)(h^2-4h+4)}{(h^2+4)^2}=\left(\frac{(h+2)(h-2)}{h^2+4}\right)^2}$$
・・・と表せるようになります。
$${b=\frac{1}{2}\left(d\mp\frac{d\sqrt{(-2d+3)(2d-1)}}{2d-1}\right)\\=\frac{h^2-2h+4}{2h^2+8}\left(1\mp\frac{(h+2)(h-2)}{h^2+4}÷\frac{(h-2)^2}{h^2+4}\right)\\=\frac{h^2-2h+4}{2h^2+8}\left(1\mp\frac{h+2}{h-2}\right)}$$
分子を少し短くできそうなので、-の方を選んでさらに整理してみます。
$${b=\frac{h^2-2h+4}{2h^2+8}\left(1-\frac{h+2}{h-2}\right)\\=\frac{h^2-2h+4}{2h^2+8}×\frac{h-2-h-2}{h-2}\\=-\frac{2h^2-4h+8}{(h^2+4)(h-2)}}$$
はい、整理できました。
$${z+b=d}$$と置いたので、$${z}$$は以下のようになります。
$${z=d-b\\=\frac{h^2-2h+4}{h^2+4}+\frac{2h^2-4h+8}{(h^2+4)(h-2)}\\=\frac{h^3-2h^2+4h-2h^2+4h-8+2h^2-4h+8}{(h^2+4)(h-2)}\\=\frac{h^3-2h^2+4h}{(h^2+4)(h-2)}}$$
一旦ここまでの計算内容を振り返ります。
$${\frac{1}{3}z^3-\frac{1}{2}z^2+\frac{a}{z}+c}$$を微分し、臨界点が$${z^4-z^3-a=0}$$の解であることが分かった。
$${a=b^4-b^3}$$と置くことで4つの臨界点の内の一つが$${z=b}$$になり、残りの3つが$${z^3+(b-1)z^2+(b^2-b)z+b^3-b^2=0}$$を満たすことが分かった。
$${z+b=d}$$と置くと$${bz=\frac{d^3-d^2}{2d-1}}$$が成り立つことがわかり、更に変形すると$${z^2-dz+\frac{d^3-d^2}{2d-1}=0}$$という2次方程式に帰着できた。
$${z^2-dz+\frac{d^3-d^2}{2d-1}=0}$$の解が有理関数で表せるようにするには、$${d=\frac{h^2-2h+4}{h^2+4}}$$と置けばいいことが分かった。
$${d=\frac{h^2-2h+4}{h^2+4}}$$と置くと$${b=-\frac{2h^2-4h+8}{(h^2+4)(h-2)}}$$になり、$${z=\frac{h^3-2h^2+4h}{(h^2+4)(h-2)}}$$という解が求まった。
3番目辺りから自分でも何をしているのかよくわからなくなっていったのですが、重要なのは「ここまでやって4次方程式の解が2個見つかっただけ」という点です。
残りの解は2次方程式で求められますが有理関数で表せる保証はなく、そもそも係数が複雑すぎて検証する気にもなりません。
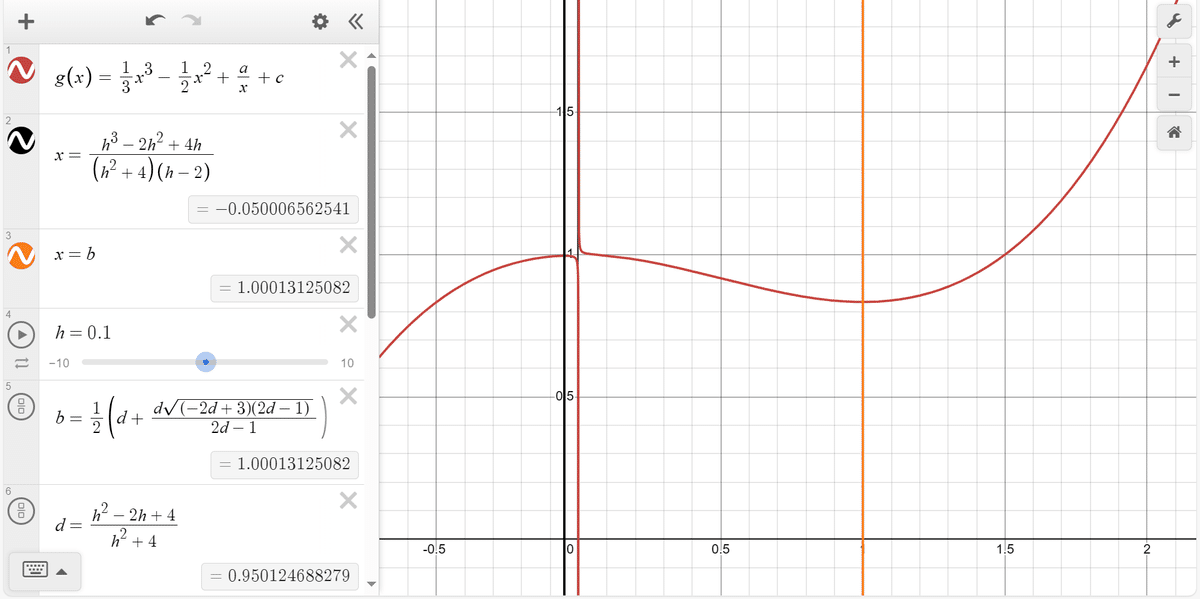

$${f(z)=\frac{1}{3}z^3-\frac{1}{2}z^2+c}$$は極端な例なのかもしれませんが、f+ε法はこんな感じで臨界点の計算が面倒臭く、多重度の調整などもやり辛いことが多いです。
$${\varepsilon}$$をもっと複雑な関数にすれば調整の自由度も上がるのですが、その分臨界点の個数も増えてしまうため上手いやり方はまだ見つけられていません。
ちなみに、私の記事のうちf+ε法で作った関数が出てくる記事は以下の通りです。
$${g(z)=z^n+\frac{a}{z}+c}$$という形の場合、臨界点を求めるための方程式は$${z^{n+1}-a=0}$$という形になり、$${n=1,3}$$のときは$${a=b^{n+1}}$$とすると全ての臨界点が簡単に求まります。
次数合わせ法
次数合わせ法は、名前の通り分数関数の次数を合わせてから係数を調整して目的の関数を作る方法です。
※ここでいう「有理関数の次数」は以下の記事に出てくる「分母の次数-分子の次数」という定義を使用します。
例えば、$${f(z)=\frac{1}{3}z^3-\frac{1}{2}z^2+c}$$を元にした関数を作るとします。
$${g(z)=\frac{bz^4+dz^3+hz^2+j}{6z+a}+c}$$とすると、$${a=h=j=0}$$、$${b=2}$$、$${d=-3}$$のとき$${f(z)}$$と一致するため、各係数をその値に近い値にすれば「$${f(z)}$$を元にした摂動系関数」になりそうです。
※後の計算で邪魔になるだけなので、$${c}$$は分数の部分に入れずに定数のままにしておいてます。分母に1次の項が無いのも同じ理由です。
今回はとりあえず$${b=2}$$、$${h=j=0}$$として$${a}$$と$${d}$$を調整してみます。
$${g'(z)=\left(\frac{2z^4+dz^3}{6z+a}\right)'\\=\frac{(8z^3+3dz^2)(6z+a)-6(2z^4+dz^3)}{(6z+a)^2}\\=\frac{48z^4+8az^3+18dz^3+3adz^2-12z^4-6dz^3}{(6z+a)^2}\\=\frac{36z^4+(8a+12d)z^3+3adz^2}{(6z+a)^2}\\=\frac{z^2(36z^2+(8a+12d)z+3ad)}{(6z+a)^2}}$$
臨界点は3つあり、そのうち1つが2重解である$${z=0}$$で、残りの2つは$${36z^2+(8a+12d)z+3ad=0}$$の解であることがわかりました。
$${36z^2+2(4a+6d)z+3ad=0}$$
$${z=\frac{1}{36}\left(-4a-6d\pm\sqrt{(4a+6d)^2-36×3ad}\right)\\=\frac{1}{36}\left(-4a-6d\pm2\sqrt{(2a+3d)^2-27ad}\right)\\=\frac{1}{18}\left(-2a-3d\pm\sqrt{4a^2+12ad+9d^2-27ad}\right)\\=\frac{1}{18}\left(-2a-3d\pm\sqrt{4a^2-15ad+9d^2}\right)}$$
$${a=\frac{m(6k-5)}{9k^2-15k+4}}$$、$${d=\frac{m(9k^2-4)}{27k^2-45k+12}}$$と置きます。
$${z=\frac{1}{18}\left(-2a-3d\pm\sqrt{4a^2-15ad+9d^2}\right)\\=\frac{1}{18}\left(-\frac{m(12k-10)}{9k^2-15k+4}-\frac{m(9k^2-4)}{9k^2-15k+4}\pm\sqrt{4a^2-15ad+9d^2}\right)\\=\frac{1}{18}\left(-\frac{m(9k^2+12k-14)}{9k^2-15k+4}\pm\sqrt{\frac{4m^2(6k-5)^2}{(9k^2-15k+4)^2}-\frac{5m^2(6k-5)(9k^2-4)}{(9k^2-15k+4)^2}+\frac{m^2(9k^2-4)^2}{(9k^2-15k+4)^2}}\right)\\=\frac{1}{18}\left(-\frac{m(9k^2+12k-14)}{9k^2-15k+4}\pm\sqrt{\frac{m^2(81k^4-270k^3+297k^2-120k+16)}{(9k^2-15k+4)^2}}\right)\\=\frac{1}{18}\left(-\frac{m(9k^2+12k-14)}{9k^2-15k+4}\pm m\right)}$$
臨界点が有理式で表せることが確認できました。
あとは$${a}$$と$${d}$$がそれぞれ0と-3に近くなるように$${k}$$と$${m}$$を調整すれば完成です。
$${\frac{m(6k-5)}{9k^2-15k+4}=0}$$、$${\frac{m(9k^2-4)}{27k^2-45k+12}=-3}$$を解くと$${(k,m)=\left(\frac{5}{6},9\right)}$$という解が出てくるので、とりあえずそれに近い値である$${(k,m)=\left(\frac{8}{9},9\right)}$$にしてみます。
$${a=\frac{m(6k-5)}{9k^2-15k+4}\\=9×\left(\frac{48}{9}-5\right)÷\left(\frac{9×64}{81}-15×\frac{8}{9}+4\right)\\=(48-45)÷\frac{64-120+36}{9}\\=\frac{27}{-20}\\=-1.35}$$
$${d=\frac{m(9k^2-4)}{27k^2-45k+12}\\=9×\left(9×\frac{64}{81}-4\right)÷\left(27×\frac{64}{81}-45×\frac{8}{9}+12\right)\\=(64-36)÷\left(\frac{64}{3}-40+12\right)\\=\frac{84}{64-120+36}\\=-4.2}$$
$${z=\frac{1}{18}\left(-2a-3d\pm\sqrt{4a^2-15ad+9d^2}\right)\\=\frac{1}{18}(2.7+12.6\pm\sqrt{7.29-85.05+158.76})\\=\frac{1}{18}(15.3\pm9)\\=1.35,0.35}$$




なお、実は$${(k,m)=\left(\frac{8}{9},9\right)}$$という数値設定は偶然見つけたもので、他の値を適当に選ぶと大抵は(有理数ではありますが)かなり汚い値になってしまいます。
f+ε法よりはマシなのですが、次数合わせ法も計算が複雑なうえに計算結果が綺麗な値にならないことがあります。
今までの記事のうち、次数合わせ法で作った関数が出てくるものは以下の通りです。
摂動系の関数の例としてよく挙げる$${\frac{z^3}{z+0.1i}+c}$$は次数合わせ法で作ったような見た目をしていますが、実際に発見した経緯は異なります。
z+ε法
z+ε法は、元になる$${f(z)}$$に対して$${g(z)=f(z+\varepsilon)}$$という関数を考える手法です。
例として、$${f(z)=\frac{1}{3}z^3-\frac{1}{2}z^2+c}$$に対して$${\varepsilon=\frac{a}{z}}$$という形の摂動項を加えた関数を考えます。
$${g(z)=f(z+\varepsilon)}$$を微分し、臨界点がシンプルな値になるような$${a}$$の値を求められるか試してみます。
$${g(z)'=\left(z+\frac{a}{z}\right)'f'\left(z+\frac{a}{z}\right)\\=\left(1-\frac{a}{z^2}\right)f'\left(z+\frac{a}{z}\right)=0}$$
一旦ここで計算を止めておきます。
まず、この時点で$${1-\frac{a}{z^2}=0}$$の解が臨界点になることがわかりますが、これは$${a=b^2}$$と置くことで簡単に求まるようになります。
他の臨界点は$${f'\left(z+\frac{a}{z}\right)=0}$$の解なのですが、$${f'(z)=0}$$の解が$${z=0,1}$$であることから
$${z+\frac{a}{z}=0}$$
$${z+\frac{a}{z}=1}$$
・・・という方程式の解であることがわかります。
どちらの式も整理すれば2次方程式になるのですが、実は「マンデルブロ集合やジュリア集合を描画する」というのが最終的な目的であれば解く必要はありません。
前者の方程式の解の1つを$${s}$$として$${z_0=s,z_{n+1}=g(z_n)}$$という数列を計算する場合、$${z_1}$$は
$${z_1=g(s)\\=f\left(s+\frac{a}{s}\right)\\=f(0)}$$
・・・という風に非常に簡単な値になり、しかも2つある解のどちらでも同じ結果になります。
ということは、$${z_0=s}$$のマンデルブロ集合は$${z_0=f(0)}$$のマンデルブロ集合と同じ形になり、結果として$${s}$$の値がわからなくても実質的に$${z_0=s}$$のマンデルブロ集合を描画できることになります。
$${z+\frac{a}{z}=1}$$の方も同じで、$${z_0=f(1)}$$とすれば事足りてしまいます。
これは$${f(z)=\frac{1}{3}z^3-\frac{1}{2}z^2+c}$$に限った話ではなく、元の関数の臨界点さえ求まればほとんど同じ手順で摂動系関数が作れます。
また、多重度を調整したり、臨界点の消失や2周期発散性などの細かい性質を維持したりするために自由度を増やすことも可能です。
例えば$${\varepsilon=\frac{a^2}{z+b}+d}$$とした場合、調節可能な係数が2つ増えるにもかかわらず計算の複雑さはほとんど変わりません。
$${f(z)=\frac{1}{3}z^3-\frac{1}{2}z^2+c}$$の場合だと、例えば$${(b,d)=(a,-a)}$$とすることで6つある臨界点の内3点を一致させて3重臨界点を作ることができます。
実際に$${a=0.2i}$$としてマンデルブロ集合を描画すると、こんな感じになります。




使用例は以下の通りです。
