
今週のフラクタル25 (c/(z^3-3z^2))
どうも、108Hassiumです。
今回は$${\frac{c}{z^3-3z^2}}$$に関するフラクタル図形をお届けします。
c/(z^3-3z^2)


$${\frac{c}{z^3-3z^2}}$$は0→∞→0というサイクルを持つ2周期発散関数ですが、$${\frac{c}{z^n-1}+1}$$等で見られた網目状の模様が現れません。
※☟「周期発散」という概念の説明がある記事
※☟$${\frac{c}{z^n-1}+1}$$に関する記事




マンデルブロ集合の細部を拡大すると、$${z^2+c}$$のマンデルブロ集合やジュリア集合に似た模様が見られます。
やはり$${\frac{c}{z^n-1}+1}$$のときのような細かい網目模様はなく、$${z^2+c}$$のマンデルブロ集合でも見られるような模様に謎の輪っかがついていたり細い線でつながっていたりといった感じです。



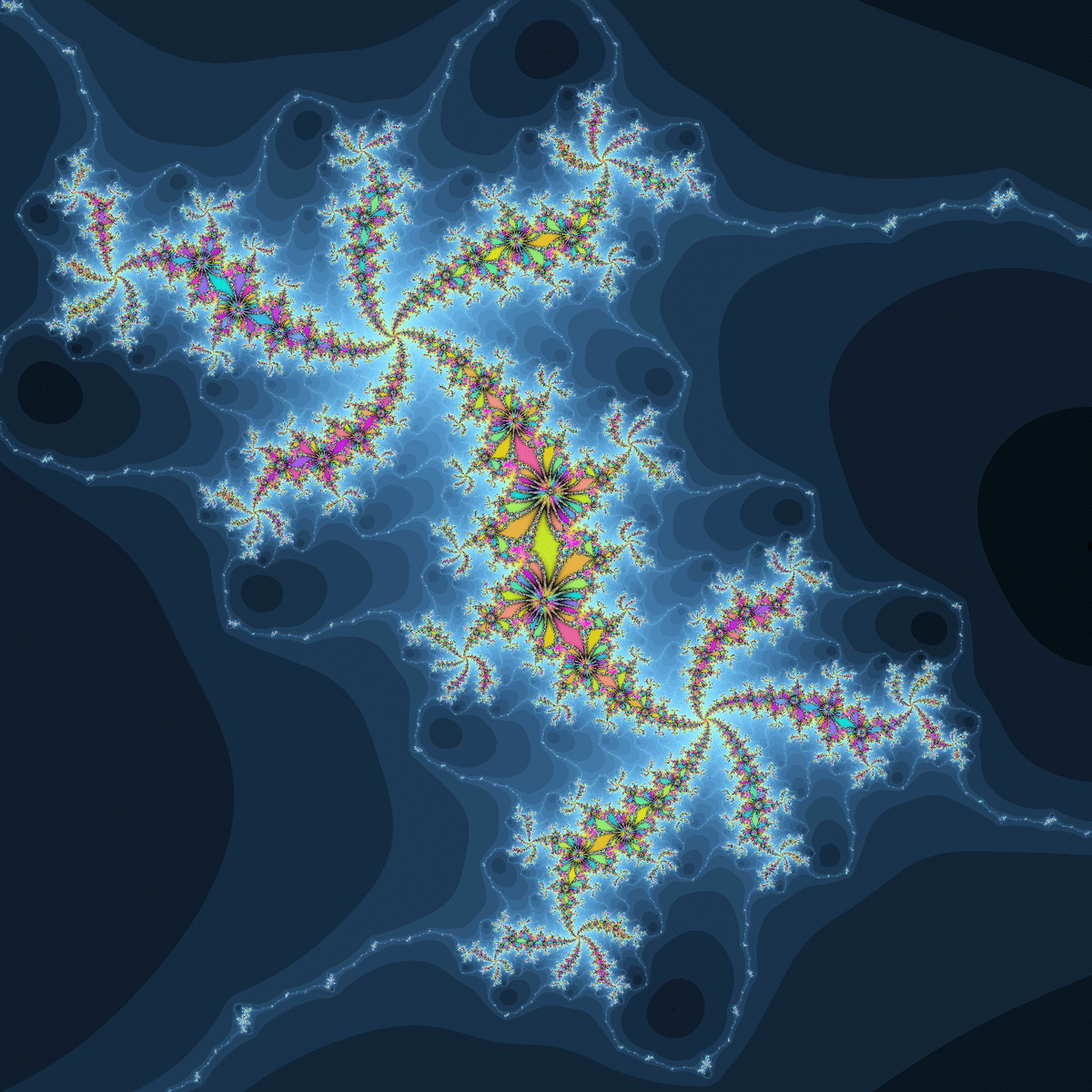
ジュリア集合もマンデルブロ集合と同じ感じで、網目模様が現れなかったり、網状になっても線が細かったりと目が非常に粗かったりして今までに紹介した周期発散関数とはかなり様子が異なります。





いつものです。
マンデルブロ集合のサイズが大きいと、長い周期のジュリア集合が多く現れがちです。
周期発散と極の位数
$${\frac{c}{z^3-3z^2}}$$は2周期発散関数でありながら周期発散関数によく見られる網状の模様が現れないのが特徴ですが、この性質は$${\frac{c}{z^3-3z^2}}$$が持つ「極」の「位数」というものと関係している可能性があります。
まず極というのは関数の特異点の一種で、有理関数の場合は分母が0になって関数の値が無限大に発散するような点のことです。
$${\frac{c}{z^3-3z^2}}$$の場合は$${z=0}$$と$${z=3}$$のときに$${z^3-3z^2}$$が0になって$${\frac{c}{z^3-3z^2}}$$が発散するので、この2点が極になります。
そして極の位数というのは極の性質を表す値で、$${a}$$が$${f(z)}$$の極であるとき$${(z-a)^nf(z)}$$が$${z=a}$$で極を持たなくなるような最小の$${n}$$が「$${a}$$における極の位数」だそうです。
$${f(z)=\frac{c}{z^3-3z^2}}$$の場合、$${z^2f(z)}$$で$${z=0}$$の極が無くなるので$${z=0}$$での位数は2、$${z=3}$$の方は$${(z-3)^1f(z)}$$で消えるので位数は1となります。


周期発散関数は∞を含むサイクルを持つ関数ですが、このサイクルには極の値も含まれています。
2周期発散関数だと極と無限遠を往復するサイクルになり、3周期以上の場合でも極から無限遠に飛ばされてからまた極の場所に戻ってくる、という構造になっています。
$${\frac{c}{z^3-3z^2}}$$での0→∞→0というサイクルも極と無限遠を行き来するサイクルですが、前述の通り$${z=0}$$における極の位数は2です。
どうも「発散サイクルに含まれる極の位数」がジュリア集合やマンデルブロ集合の見た目と関係しているようで、位数が1のときは$${\frac{c}{z^n-1}+1}$$のような網状の見た目に、2以上だと今回のように糸状になるっぽいです。
例えば$${\frac{c}{z^4-2z^3}}$$の$${z=0}$$の極の位数は3ですが、この関数でも$${\frac{c}{z^3-3z^2}}$$と同様に糸状の模様が現れます。
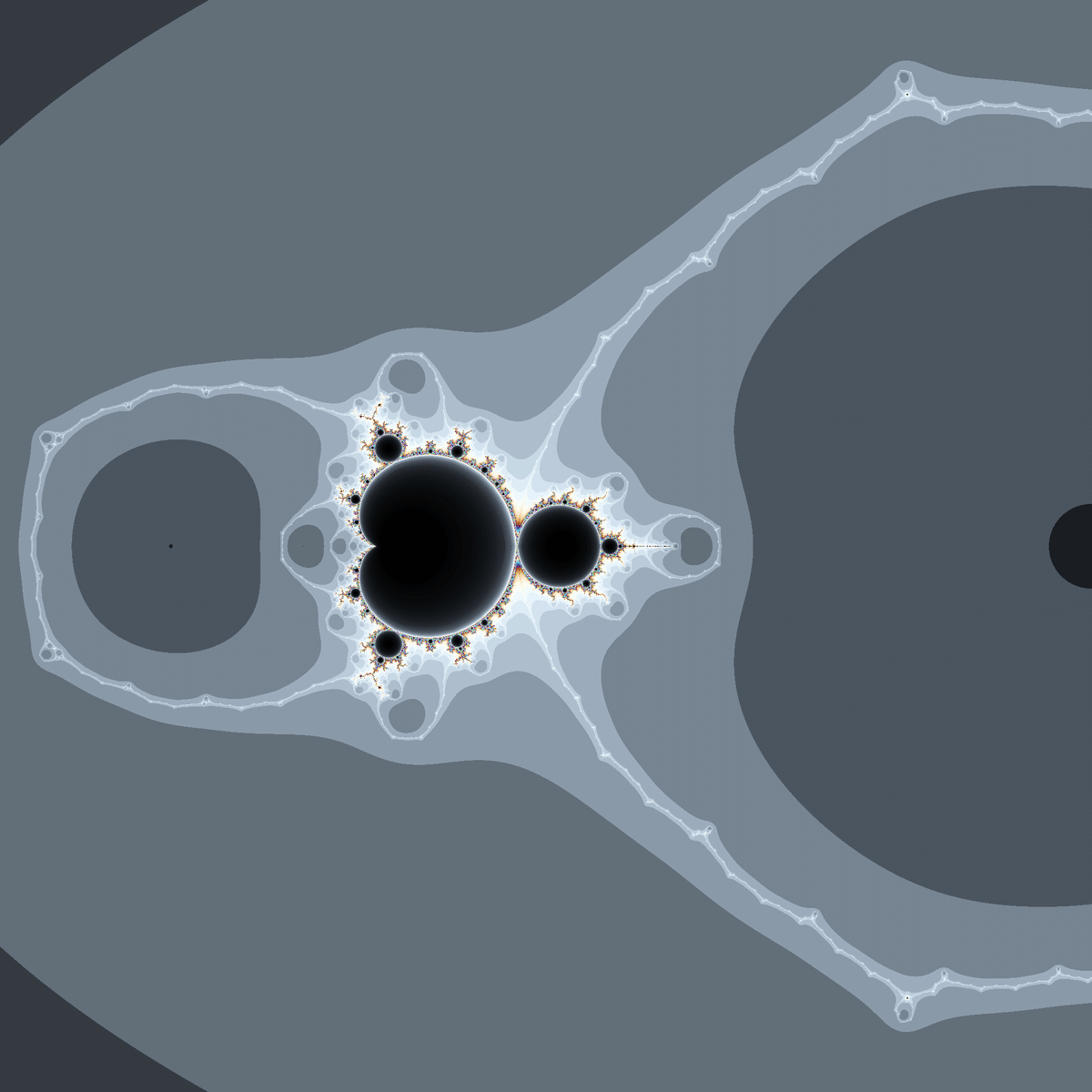
また、$${\frac{c}{z^3-3z^2}+3}$$という関数は、定数項があることによって位数1の方の極から発散していく(=3→∞→3というサイクルを持つ)ようになっており、$${\frac{c}{z^n-1}+1}$$と同じような網状の模様が現れます。

$${f(z)=\frac{a}{z^3-3z^2}+b}$$という形をした3周期発散関数は、2つの極のうちどちらを発散サイクルに含めるかで2種類に分かれます。


ご覧の通り、位数2の極をサイクルに含む方に糸状の模様が現れています。
ちなみに過去の記事で紹介した周期発散関数はほとんどが位数1の極しか持ちませんが、$${\frac{1}{z^2}-1}$$は位数2の極を持つ3周期発散関数であり、ジュリア集合は糸状(鎖状?)になっています。

こういった現象が発生する仕組みは不明(そもそも感覚に基づく非数学的現象なので解明のしようがない)ですが、何か数学的な背景があるとすれば臨界点の多重度の話と関係あるんじゃないか、と思っています。
※☟臨界点の多重度の話が載っている記事
