今週のフラクタル74　(c(z^2-con(z)))

どうも、108Hassiumです。

今回は$${c(z^2-\text{con}(z))}$$($${\text{con}(z)}$$は$${z}$$の複素共役)に関するフラクタル図形をお届けします。

c(z^2-con(z))

☝c(z^2-con(z))のマンデルブロ集合(z_0=0.5)

マンデルブロ集合です。

☝(1.04+0.51i)(z^2-con(z))のジュリア集合

☝(-0.29+1.34i)(z^2-con(z))のジュリア集合

☝1.1i(z^2-con(z))のジュリア集合

☝(-0.3+1.4i)(z^2-con(z))のジュリア集合

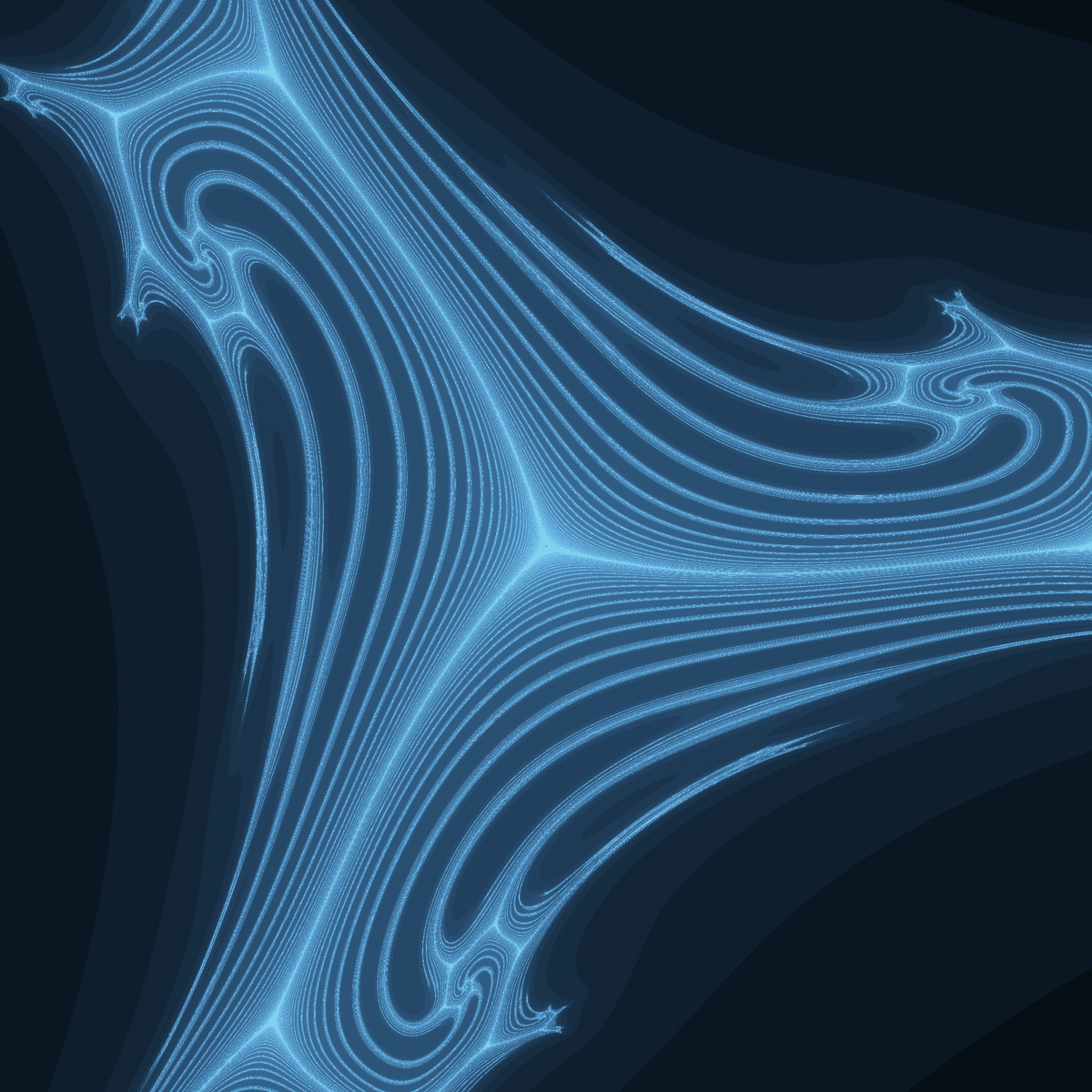
ジュリア集合は、3回回転対称である点が特徴です。

☝(-0.89+1.14i)(z^2-con(z))のジュリア集合

☝(-0.23+1.23i)(z^2-con(z))のジュリア集合

☝(1.68+0.12i)(z^2-con(z))のジュリア集合

$${z_0=0.5}$$と$${z_0=\frac{-1+\sqrt{3}i}{4}}$$が別の吸引的サイクルに収束するジュリア集合です。

ジュリア集合の形状は3回回転対称ですが、収束領域の分かれ方は$${c\left(\frac{z^2}{2}+\frac{1}{z}\right)}$$と同じように非対称になるようです。

※☟$${c\left(\frac{z^2}{2}+\frac{1}{z}\right)}$$のジュリア集合について触れた記事

☝(1.48+0.16i)(z^2-con(z))のジュリア集合

☝(0.98+0.5i)(z^2-con(z))のジュリア集合

☝(1.7+0.15i)(z^2-con(z))のジュリア集合

$${z_0=0.5}$$と$${z_0=\frac{-1-\sqrt{3}i}{4}}$$が別の吸引的サイクルに収束するジュリア集合です。

☝(1.08+0.47i)(z^2-con(z))のジュリア集合

☝(-0.95+i)(z^2-con(z))のジュリア集合

☝(-0.38+1.32i)(z^2-con(z))のジュリア集合

☝(-0.91+1.41i)(z^2-con(z))のジュリア集合

$${z_0=0.5,\frac{-1\pm\sqrt{3}i}{4}}$$がそれぞれ別の吸引的サイクルに収束するジュリア集合です。

☝(0.07+0.91i)(z^2-con(z))のジュリア集合

☝(0.8+0.51i)(z^2-con(z))のジュリア集合

☝(0.78+0.52i)(z^2-con(z))のジュリア集合

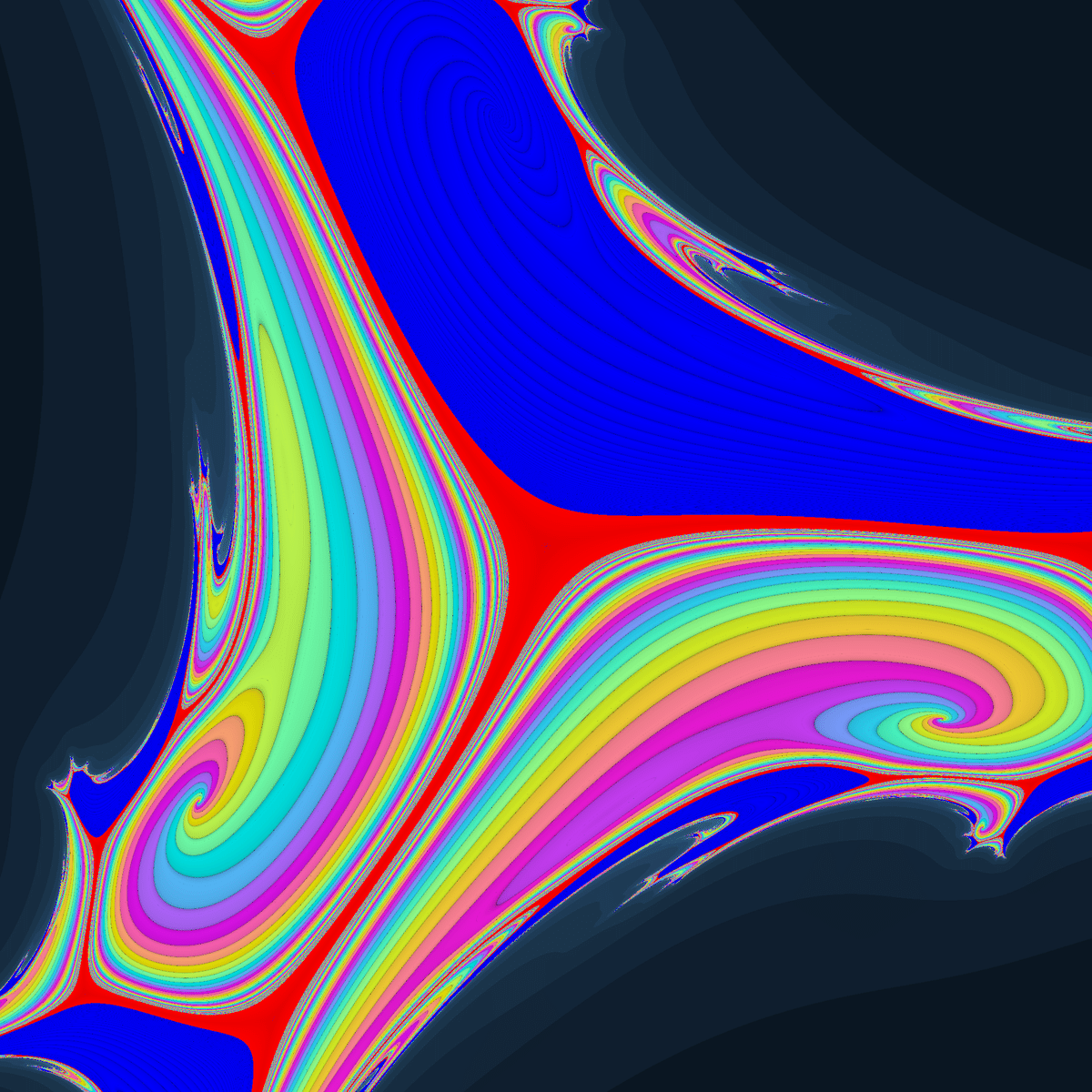
0に収束する領域のあるジュリア集合です。

☝(-0.81+1.36i)(z^2-con(z))のジュリア集合(5サイクル)

☝(-0.64+1.38i)(z^2-con(z))のジュリア集合(7サイクル)

☝(-0.83+1.33i)(z^2-con(z))のジュリア集合(8サイクル)

吸引的サイクルがたくさんあるジュリア集合です。

☝(1.24+0.4i)(z^2-con(z))のジュリア集合

☝(-0.5+1.33i)(z^2-con(z))のジュリア集合

非周期的サイクルに収束する領域のあるジュリア集合です。

☝(-0.9+0.53i)(z^2-con(z))のジュリア集合とストレンジアトラクター

☝(-0.9+1.3i)(z^2-con(z))のジュリア集合とストレンジアトラクター

☝(-0.9+0.5i)(z^2-con(z))のジュリア集合とストレンジアトラクター

☝(-0.92+0.57i)(z^2-con(z))のジュリア集合とストレンジアトラクター

☝(-1+0.9i)(z^2-con(z))のジュリア集合とストレンジアトラクター

☝(-1+0.8i)(z^2-con(z))のジュリア集合とストレンジアトラクター

☝(-0.97+0.65i)(z^2-con(z))のジュリア集合とストレンジアトラクター

☝(-1+1.1i)(z^2-con(z))のジュリア集合とストレンジアトラクター

☝(-0.9+1.5i)(z^2-con(z))のジュリア集合とストレンジアトラクター

ストレンジアトラクターは、3回回転対称になったりならなかったりするようです。