
マンデルブロ集合のマンデルブロ集合?
どうも、108Hassiumです。
最近ある関数族のマンデルブロ集合に関するちょっと面白い現象を発見したので記録しておこうと思います。
c(z+1/z)
まず、これが$${c(z+\frac{1}{z})}$$のマンデルブロ集合です。

単位円の中にさらに小さな円状の領域が内接しています。

よく見ると$${z^2+c}$$のマンデルブロ集合に似た形が散らばっています。
モザイク状の領域は、$${z_n}$$が非周期的になる(途中で大きな値が出るので、発散すると誤判定されている)領域っぽいです。
$${c(z+\frac{1}{z})}$$の臨界点は2つありますが、どちらを初期値にしても同じ形のマンデルブロ集合になるようでした。
本題とはあまり関係ありませんが、ジュリア集合も載せておきます。




各収束領域とジュリア集合の周期の関係は以下のようになっています。(上半分の数字は下と同じなので省略しています)

以下の記事で$${z^2+c}$$のマンデルブロ集合に関する似たような図が出てきましたが、それと比べるとかなり不規則になっています。
d(z+1/z)+c
続いて、$${d(z+\frac{1}{z})+c}$$($${d}$$は定数)のマンデルブロ集合を見てもらいます。
このタイプのマンデルブロ集合は$${d}$$の値によって見た目が大きく異なるため、$${d}$$の範囲によっていくつかに分けて紹介します。
1<|d|


$${1<|d|}$$の場合、マンデルブロ集合は$${z^2+c}$$のものと同様に内側と外側に分かれた形になります。


$${d}$$の範囲によっては、収束領域のサイズがものすごく大きくなるようです。

$${d}$$が実数ではなくなると、実軸について非対称なマンデルブロ集合になるようです。
ちなみに、初期値を-1にした場合は原点を中心に180度回転させた形のマンデルブロ集合が出来上がります。(これは$${d}$$の範囲とは関係ない性質です)



$${|d|}$$が1に近いと$${z_n}$$の発散が遅くなるので、外側がやたらカラフルになります。
ところで、以下の記事には「$${d(z+\frac{1}{z})+c}$$のジュリア集合は、$${|d|<1}$$のときだけ変な領域が現れる」という趣旨の記述があります。
この記事の投稿後、変な領域と$${d(z+\frac{1}{z})+c}$$のマンデルブロ集合について以下のような経験則を発見しました。
経験則1:$${f(z,a)}$$のジュリア集合が変な領域を持つならば、$${f(z,c)}$$は複数の臨界点を持ち、定数$${a}$$は臨界点を初期値とする複数個の$${f(z,c)}$$のマンデルブロ集合の共通部分の中にある。
経験則2:$${d(z+\frac{1}{z})+c}$$のマンデルブロ集合は、$${1<|d|}$$であれば共通部分を持たない。
もしこれらが両方とも成り立てば、「$${d(z+\frac{1}{z})+c}$$のジュリア集合は、$${1<|d|}$$のとき変な領域を持たない」といえそうです。(そもそも変な領域という概念が定式化できていないので無理な話ですが)
|d-0.5|<0.5


$${|d-0.5|<0.5}$$のときは、$${d(z+\frac{1}{z})+c}$$のマンデルブロ集合は発散領域を持たなくなります。
周期サイクルへの収束速度を使って収束領域を彩色すると、端のある1本の曲線に沿って円状領域が並んだ形が現れます。



$${d}$$の虚部の値によっては、S字状の曲線になることもあるようです。
|d+0.5|<0.5


$${|d+0.5|<0.5}$$の場合、$${c(z+\frac{1}{z})}$$のマンデルブロ集合で見られたようなノイズ状の不安定領域が出現します。
また、細部をよく観察すると複数の収束領域が重なっていたり、くっついたりひび割れたりといった異様な見た目の部分構造が見られます。
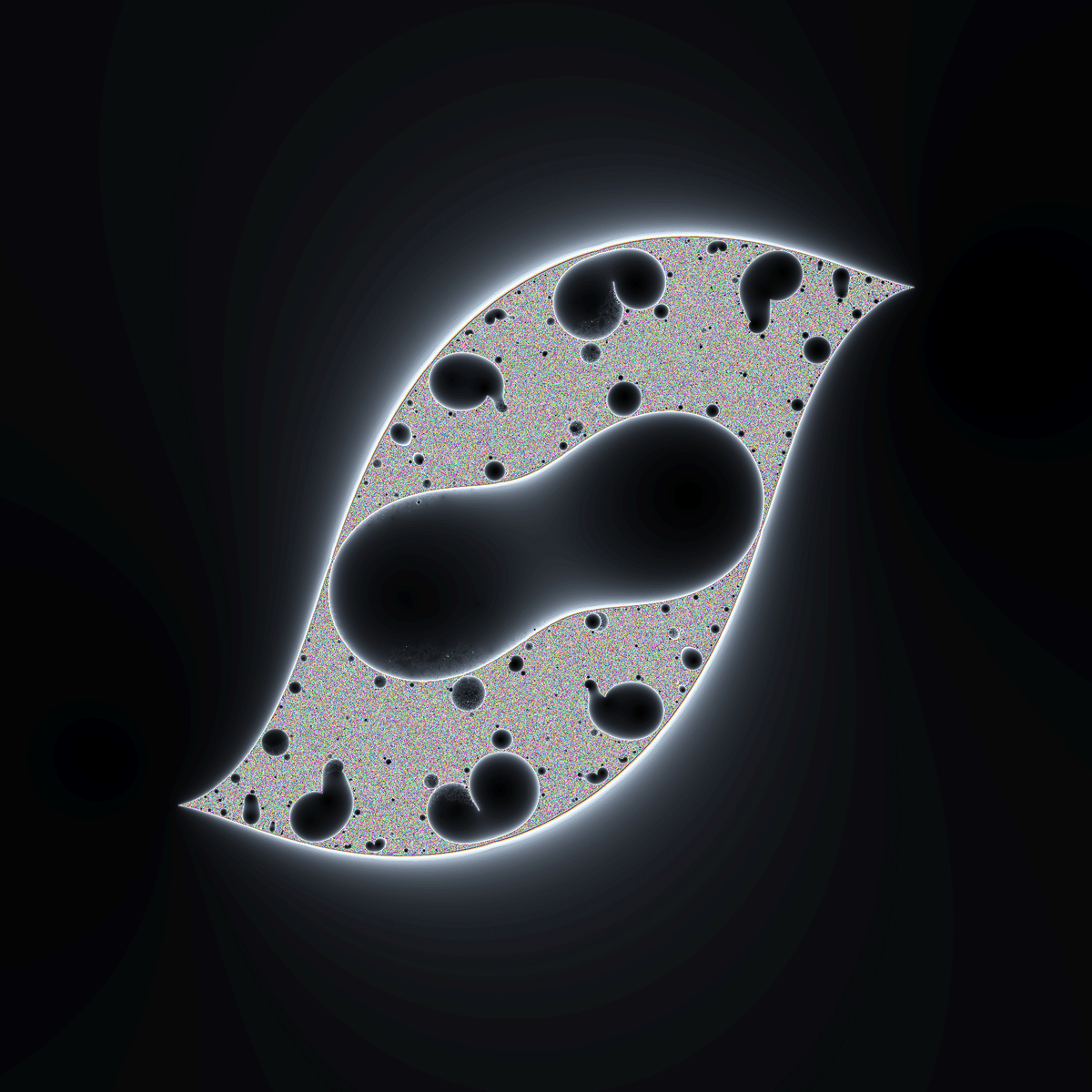

不安定領域も含めた全体の形は点対象に見えますが、細部の特徴に注目すると微妙に対称性が崩れています。
さて、今まで$${d}$$の範囲は不等式だけで表してきていましたが、複素平面上に図示すると以下のようになっています。

赤が$${1<|d|}$$、青が$${|d-0.5|<0.5}$$、緑が$${|d+0.5|<0.5}$$の範囲です。
実はこの図形、冒頭で紹介した$${c(z+\frac{1}{z})}$$のマンデルブロ集合の一部になっています。

2つの小さい円が円状領域の輪郭に、大きい円が不安定領域と発散領域の境界線になっています。
その他
「不安定領域と収束領域に分かれたマンデルブロ集合になる」という性質をあたかも$${|d+0.5|<0.5}$$のときだけの性質であるかのように紹介しましたが、実はそうではありません。
$${|d+0.5|<0.5}$$でなくても、$${|d|<1}$$かつ$${0.5<|d-0.5|}$$であれば不安定領域のあるマンデルブロ集合になることがあります。





$${c=0}$$の点、つまり画像の中央をよく見ると、
不安定領域の中にある($${d=0.1+0.4i}$$)
二つの収束領域が重なっているような領域の中にある($${d=-0.5+0.51i\ ,0.2+0.5i}$$)
重なっていない収束領域の中にある($${d=-0.2+0.5i\ ,0.5+0.8i}$$)
の3種類に分類できそうに見えます。
最初のケースは$${d}$$が$${c(z+\frac{1}{z})}$$のマンデルブロ集合の不安定領域にある場合に対応し、残りの二つは「$${z_{n+1}=c(z_n+\frac{1}{z_n})}$$が$${z_0=1,-1}$$で異なるサイクルに収束するかどうか」と関係があるようです。
$${c(z+\frac{1}{z})}$$のマンデルブロ集合を「$${z_0=1,-1}$$で異なるサイクルに収束するかどうか」で色分けすると、以下のようになります。

青が異なるサイクルに収束する領域で、赤が同じサイクルになるほうです。(計算精度の問題により青の領域が赤の領域にハミ出している所がありますが、本来なら円状領域ごとに色分けされます)
-0.5+0.51iと0.2+0.5iはどちらも青の領域に、-0.2+0.5iと0.5+0.8iは赤の領域の中にあります。
ところで、このセクションの冒頭で「$${|d|<1}$$かつ$${0.5<|d-0.5|}$$であれば不安定領域のあるマンデルブロ集合になることがある」と言いましたが、どうやら$${|d|<1}$$かつ$${0.5<|d-0.5|}$$であっても不安定領域が現れないこともあるようです。




$${|d-0.5|<0.5}$$のときと同様に、有限長の曲線に沿って円状領域が並んだ構造が現れます。
曲線の本数は$${d}$$の値によって異なりますが、どうも$${c(z+\frac{1}{z})}$$のマンデルブロ集合上で$${d}$$が属する収束領域に対応する周期が$${p}$$のとき、曲線の本数は何故か$${p-2}$$に一致するっぽいです。
例えば$${c(z+\frac{1}{z})}$$のマンデルブロ集合上では0.86+0.5iという値は12周期の収束領域の中にありますが、$${(0.86+0.5i)(z+\frac{1}{z})+c}$$のマンデルブロ集合には「$${|d-0.5|<0.5}$$のときみたいな曲線」が10本出現します。
このように不安定領域(と発散領域)を持たないマンデルブロ集合は$${c(z+\frac{1}{z})}$$のマンデルブロ集合の収束領域と関連した性質を持つのですが、「不安定領域が出現しない条件」自体は$${c(z+\frac{1}{z})}$$のマンデルブロ集合の性質とは微妙にズレているようです。
不安定領域が出現しないような$${d}$$の値をほんの少しだけズラすと、円状領域から出たわけではないのに不安定領域が出現することがあります。


この現象を可視化するために、以下のような図を描画してみました。

この図は「0.5+0.8iを中心として、『$${d}$$の値を0.004ずつずらした$${d(z+\frac{1}{z})+c}$$のマンデルブロ集合』を50×50に並べたもの」で、各マンデルブロ集合は収束領域を黒、不安定領域と発散領域を白で塗ってあります。
真っ黒な領域(=$${d(z+\frac{1}{z})+c}$$のマンデルブロ集合が不安定領域も発散領域も持たなくなる領域)は丸い形をしており、$${c(z+\frac{1}{z})}$$のマンデルブロ集合の収束領域の形に似ているように見えますが、同じ範囲のマンデルブロ集合と見比べてみるとサイズが明らかに違うことがわかります。

どうやら$${c(z+\frac{1}{z})}$$のマンデルブロ集合は、円状領域の中にさらに不可視の円状(?)領域が存在し、$${d}$$がその中にあるときだけ$${d(z+\frac{1}{z})+c}$$のマンデルブロ集合が不安定領域も発散領域も持たなくなるようです。
おわり
というわけで、以上「$${c(z+\frac{1}{z})}$$のマンデルブロ集合が$${d(z+\frac{1}{z})+c}$$のマンデルブロ集合の性質を表していると思ったら微妙にうまく対応していなかった話」でした。
・・・実は今回あえて触れないようにしていた$${d}$$のグループがあって、それはそれで面白いのでいつか別の記事のおまけとかで触れようと思います。
それではさようなら。

追記(2023/06/11)
☟続き
