
今週のフラクタル36 (con(z)^8+c)
どうも、108Hassiumです。
今回は$${\text{con}(z)^8+c}$$($${\text{con}(z)}$$は$${z}$$の複素共役)に関するフラクタル図形をお届けします。
con(z)^8+c

$${\text{con}(z)^n+c}$$のマンデルブロ集合は$${n+1}$$回回転対称なので、$${\text{con}(z)^8+c}$$のマンデルブロ集合は9回回転対称になります。



拡大図です。
$${\text{con}(z)^8+c}$$のマンデルブロ集合に似た形だけでなく、$${z^8+c}$$のマンデルブロ集合に似た飛び地もたくさん見られます。




ジュリア集合の特徴に関しては、収束領域の形状や回転対称性などが$${z^8+c}$$とよく似ています。
※☟$${z^8+c}$$の記事




$${\text{con}}$$系関数の特徴がわかりやすく出ているジュリア集合です。
※☟$${\text{con}}$$系関数の特徴の説明がある記事






飛び地型のジュリア集合が複雑で美しい点は、$${z^8+c}$$と共通する特徴です。

2種類の異なるアーチ形接点が混在するジュリア集合です。



アーチ形接点からもう1本枝が生えているジュリア集合です。
このような特徴のあるジュリア集合は今までは$${-\frac{c^2-3}{c^2\text{con}(z)^3-3\text{con}(z)}+1}$$等の分数関数を基にした関数でしか見たことが無かったので、単純な多項式関数で見られたのはかなり意外でした。
※☟$${-\frac{c^2-3}{c^2\text{con}(z)^3-3\text{con}(z)}+1}$$のジュリア集合が載っている記事





いつものです。
枝付きアーチ形接点
マンデルブロ集合上で$${\text{con}(z)^8+0.57+0.72i}$$や$${\text{con}(z)^8+1+0.27i}$$のような「アーチ形接点に枝が生えているジュリア集合」に対応する場所を観察してみます。


他の場所もいくつか調べてみたところ、どうやら以下のような共通点があるようでした。
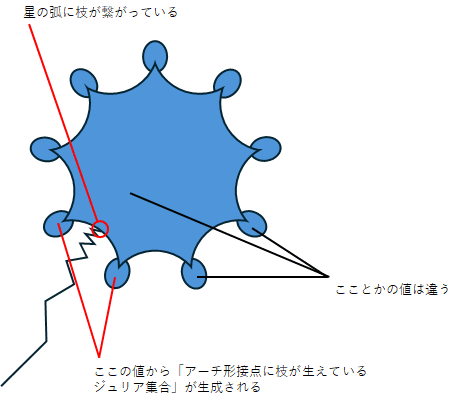
「もしや」と思って調べてみたところ、$${\text{con}(z)^2+c}$$でも以下のように「アーチ(略)」を見つけることができました。


