
理系勉強の最短ルート
こんにちは。
卵かけてないご飯です。
今回は、ビジネスプランではなく「理系科目の勉強法」について書きたいと思います。
誰やねん。お前は!
えープロフィールに書いている通り単なる「理系大学生」です。ですが、ちょっと異色の研究をしていまして、「ADHDを超越した話」を読んでくださった方ならわかるかもしれませんが、論文を読むことが日課だったんです。そこで、教育関係にも興味があったので、色々と調べてたわけなんです。また、塾講師として理系科目を教えていた経験もありますので、まぁ見るだけ見てほしいなと。思いますね。
たくさん解く。
はい。またこいつもかよ。って思いますよねー。でもなんだかんだ、解きまくるのがベストプラクティスです。なんのためにときまくるのかと言いますと、問題の傾向を知るためです。
ここで、一つ例を考えてみましょう。考えてみてくださいね。
「あなたは、生まれてからすぐにちゃんとしたご飯を食べ始めましたか?」
いやーなわけないですよね!最初は固形物,生物でないものからスタートし、徐々に今に至るわけですよね。そりゃそうっすよね。喉に詰まらせるとか危ないですもんね。でも、これって勉強にもいえるのではないですか??最初っからめちゃむずい問題を解き始めるのはナンセンスです。最初は基礎から始めて問題をグループ分けして手順を明確にした上で、難問に挑むのです。そうすれば、大きな失敗には至りませんから。普通に、問題数をこなしていけば、これ!あの問題の改題やん!っていうのが楽しくてたまりませんよ。
問題の単純化
はい。ここからが塾講師っぽいことを言いますね。
「難しい問題 = 簡単な問題の集合体」
何言ってんの、こいつってなりますよね。そこで、とっておきの問題を用意しました。
高さ144mの高層ビルの屋上までエレベータで昇った。はじめ、地上で静止していたエレベータは最初の6秒間までは一定の加速度αで,次の8秒間は一定の速さで上昇して高さ99mまで達し、あとは一定の加速度で減速しながら上昇して屋上についた。
最初から6秒間の運動をエレベータの高さyと速さvをαと出発してからの時間tを用いてそれぞれ求めよ。
加速度αを求めよ。
一定の速さで上昇した距離はいくらか。
はい。嫌いな人は嫌いな力学の〇〇直線運動の問題ですよね。。そこで、問題が長いので分解します。
まず、問題の大きな運動としては、144mエレベータで登る
その中で、以下の順番で運動が変化すると。
地上で静止。
6秒間加速度αで等加速度直線運動
8秒間等速直線運動(99mまで達する)
一定の加速度で等加速度直線運動(減速)
はい。ここまで分解できますね。そこで、(1)をみてみます。この問題では、以下のように問題を解釈できますね。
求めるものは「高さy」と「速さv」の2つ
使っていい文字は、加速度αと時間t
では、問題を解く前処理ができたところで、解いていきますか。まず重要なことは、公式を覚えるのではなく使えるようになること。何言ってんだとなるんですが、例えばですね、以下の公式覚えてますか??
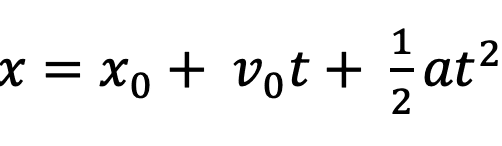
はいこれ、暗唱した人いるんじゃないですか??じゃあ、これ、いつ使うんですか。ってことなんです。答え言いますね。加速度,速度,位置,時間が全部関係している時に使います。これは、問題ガンガン解いた結果、気づいたことではあるんですけど、3つ公式あってこれを選ぶ決定プロセスを明確にするのも重要ですね。
というわけで、この公式を使っていくんですけど、まずは高さを求めたいんで、高さは変位に当たりますね。そこで、他の要素を代入すれば完結すると。。まだ、基礎問題にあたるので、プロセスが一つなのがありがたいですが、問題を単純化し、運動を分ける。その上で、公式の使い分け(決定プロセス)を単純化する。あとは、代入。って感じになるわけです。だからこそ1つの難しい問題として捉えるのではなくプロセスを3段階に分けた集合体として捉えるべきなんです。このプロセスはどの複雑な問題にも応用できるので、覚えておくと良いでしょう。あとは、前処理をどの程度丁寧にできるかですね。こんな感じに簡単やんこれ!!って考えると、難しくなくなりますね。
おわりに
今回も読んでくださりありがとうございました。
やはり、理系科目って難しいので参考になると嬉しいです!
次の投稿もぜひ楽しみにしていてください。
今回の問題をノートに解くとしたら。。
今回使った問題をノートにまとめるとしたら。。と考えたので、一応載せときますね!!受験生の方もそうじゃない方も頑張ってください!!
この記事が気に入ったらサポートをしてみませんか?
