
数学やさんの「きれい」~二重根号編~
高校くらいになると環境によってはにわかに聞こえてくる言葉。
数学の問題を解くときの「きれい」かどうか、の問題。
残念ながら、私は数式に「きれい」を感じ取る人間なので、そっちの立場の人間であることを念頭に置きながら、「きれい」を感じてみよう。
二重根号は「きたない」
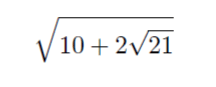
数学やさんのいう「きれい・きたない」は置いといたとしても、ルートの中のルートは「きたない」。
ここでいう「きたない」は、「不快」とか「なんのこっちゃわからん」とか、単純な美醜とは異なる意味合いが含まれる。
少なくとも、上の式を見つめていて「大体どれくらいの数か」とかを考え始めたら、日本国民の4分の1はアレルギー反応を起こしてしまう気がする。
できる限り分かりやすい形にしていって、見つめることができる形にしよう。
ルートの原則が大事
ルート(平方根)の原則。
それは$${\sqrt{a^2} = a}$$ ということ(正確には、$${a>0}$$をつけるべきかな)。
先程の二重根号の中身をこんな風に式変形できたらいいな、ということ。

「中身が2乗になれば、とにかくルートはとれる。」
そのためにわざわざ因数分解をして、2乗の形を作り出す。
単純な発想だが、このルートの原則がとても重要になる。
実際の作業を追っていくと

この式を、$${\sqrt{(a+b)^2}}$$ の形にしたい。
「少なくとも、ルートの中身にはルートがいるはず!」ということに気付くことができれば、これは半分クリア、といったところ。
$${a^2+2ab+b^2 = a^2+b^2+2ab}$$ となるので、見比べれば、
掛けて$${\sqrt{21}}$$ になる数字の組み合わせを見つけてくればいい。

ここまでくればもう少し。
$${ \sqrt{(\sqrt{7}+\sqrt{3})^2 } }$$と因数分解できる。
ということは、

二重根号はこのように外す。
とにかく「2乗したらルートが取れる」に向かって、数字を調整していく。
油断は禁物(その1)
思いついた順に数字を書くのはとても危ない。

プラスとマイナスが変わっているだけだが、これだけでもミスは増える。
決して$${ \sqrt{3} - \sqrt{7} }$$ としてはいけない。
なぜなら、$${ \sqrt{3} - \sqrt{7} }$$ は負の数、上の式は正の数。
大きい数字を必ず先に書いておくこと。
これが癖づいていることで、もったいないミスはぐんと減る。
そんでもって、これが正しい答え。

油断は禁物(その2)
$${a^2+b^2+2ab}$$ の「2」が重要だということ。

これを見ていて、数字の組み合わせが浮かべばいい。
しかし、一般ピーポーの私はなんも浮かばない。
とっかかりが見つからない。
だから、公式通り、「2」にしてあげればいい。

そしたら、$${ \sqrt{ (\sqrt{6} + \sqrt{2})^2 } }$$ とでてきて、答えこれ。

油断は禁物(その3)
「2」が重要なので、とにかく「2」を作ることを最優先する。

「2」がでてこない場合は無理やり作ってしまえ、ということ。

無理やり「2」を生み出すことができれば、二重根号に怖いものはなし。
$${ \sqrt{ (a+b)^2 } }$$ の形に帰着することができれば、「きたない」式もきれいに分かりやすくなる。
