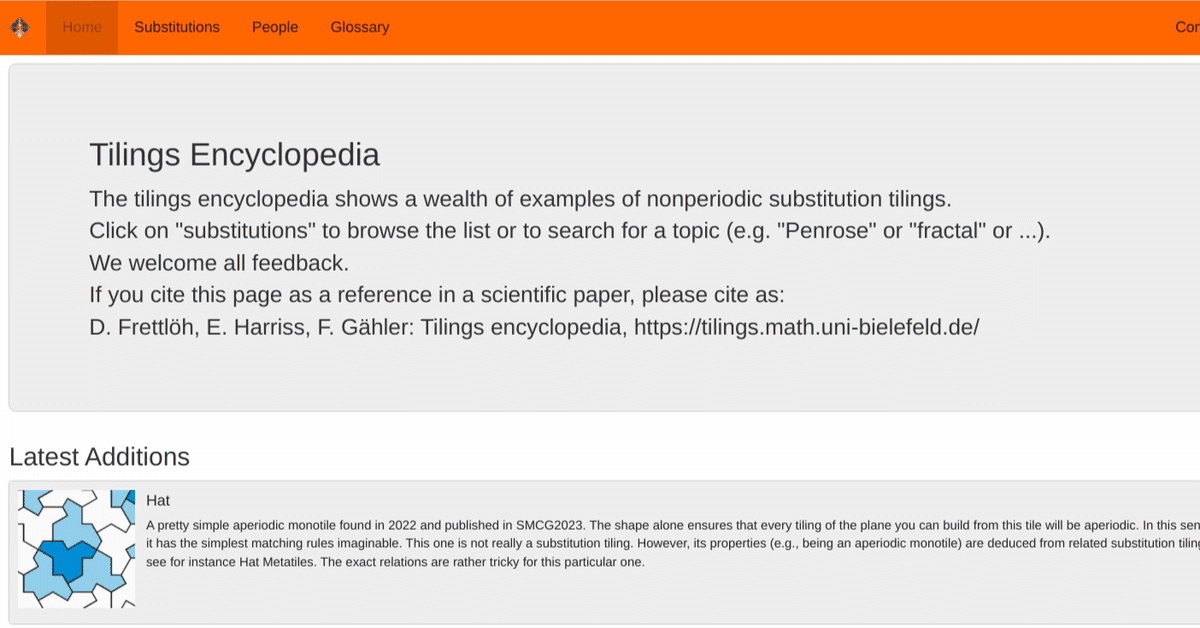
アインシュタインタイルを愛でると「Tiling Encyclopedia」に当たる。
前回の記事はこちら。
今回は、後日談です。
Tile(1,1)はこんなタイルでした
前回はこのタイルを愛でていました。
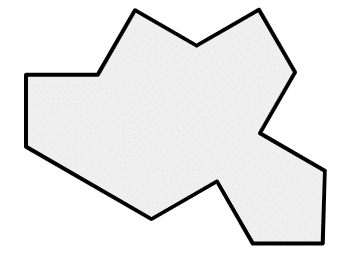
論文「An aperiodic monotile」では、Tile(1,1)と呼ばれている(「HAT」とか「TURTLE」とかの愛称は特にない)ものです。
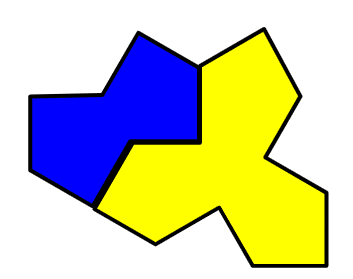
このタイルは、2つの点対称の図形に分ける事ができます。
記事をアップから数日経過しまして、もう何度もこのシリーズではお世話になってしまっている、、日本テセレーションデザイン協会の代表でもある数学者の荒木義明さんのツイートがありました。
Tile(1,1)も2回対称と3回対称に分けられる
— Yoshiaki Araki 荒木義明 (@alytile) May 10, 2023
この形は周期的なタイリングができる連続変形の中でも例外的なものです。
また二つに分けたタイルで、別の非周期タイリング「Wheel Tiling」を構成できることでも知られています。https://t.co/djoxjndlZg
Symmetrical decoration of tile set of wheel tiling,
— Yoshiaki Araki 荒木義明 (@alytile) May 11, 2023
and related decorations of Tile(1,1), a periodic tile in the contineum of aperiodic monotiles . pic.twitter.com/ueCVpTTERy
ツイートにある「Wheel Tiling」。
これは一体何?となりまして、検索してみたところ見つかりました。

おお!
まさしく、Tile(1,1)の2つの片割れが犇犇しております。
Tiling Encyclopedia
上の画像は、「Tiling Encyclopedia」の項目「Wheel Tiling」から引用しました。
【ホーム画面の紹介文を引用】
The tilings encyclopedia shows a wealth of examples of nonperiodic substitution tilings.
【翻訳】
タイリング百科事典には、非周期的な置換タイリングの例が豊富に示されています。
最新の項目は、まさに「HAT」です。
「Substitutions」の項目で、さまざまな非周期的置換タイリングを見ることができます。
現在のところ200項目あります。
「Wheel Tiling」は、アルファベット順で並べると最後尾の項目になります。
とにもかくにも、ナンノコッチャかよくわからない人も、たくさんの画像を眺めるだけでも楽しめます。
締め
ということで、今回は簡単に。
「Tiling Encyclopedia」だけでもおぼえて帰ってください。
では。
