アインシュタインタイル「HAT」と「TURTLE」の向こう側のタイルを愛でる。とにかく愛でてみる。

前回の記事はこちら。

今回は、前々回の続きとなります。

向こう側とは？

前々回の記事でも登場した、論文「An aperiodic monotile」から、１１ページにある、以下の図。

（Tile(x,x)と名付けている）単一のタイルを平面に敷き詰めた図です。
前々回は、Tile(1,1)を愛でたわけですが、今回はTile(1,4)とTile(4,1)を愛でてみよう、です。
ちなみに、非周期敷き詰めモノタイルはTile(1,$${\sqrt{3}}$$)こと「HAT」、
Tile($${\sqrt{3}}$$,1)こと「TURTLE」だけではなく、

Tile(0,1)からTile(1,1)の間の変化途中のタイル、
Tile(1,1)からTile(1,0)の間の変化途中のタイル、
全部非周期敷き詰めモノタイル

というとんでもないことになっております。
そういった意味では、Tile(1,4)とTile(4,1)はとりわけ特別なタイルではありませんが、図で登場した以上、愛でるのです。

Tile(4,1)とTile(1,0)

まずは、Tile(4,1)から。
１枚だけ抜き出すと、こんなかたち。

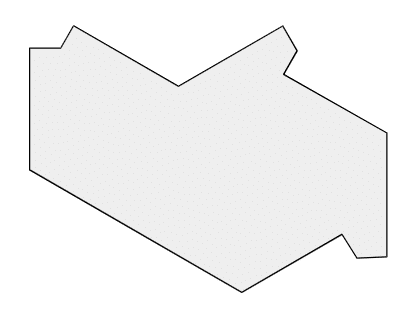
短い辺の長さを１とすると、長い辺は４、もっと長い辺は２倍の８になります。
この図形も「HAT」や「TURTLE」と同様に、「ヘリコプター」――２つの点対称図形にわけることができます。

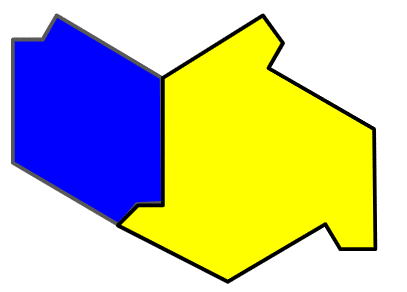
さて、いままで「ヘリコプター」化したタイル４つを並べてみます。

左から、
・Tile(1,$${\sqrt{3}}$$)こと「HAT」
・Tile(1,1)
・Tile($${\sqrt{3}}$$,1)こと「TURTLE」
・Tile(4,1)
です。
一連の図形の変化をみると、一番右にくるTile(1,0)は

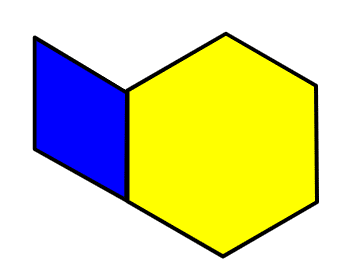
と、２つの図形にわけることができます。
というか、回転主翼（黄色）は正三角形を６個、回転尾翼（青）は正三角形を２個組み合わせた図形です。
そして、以下の５つの部分（ただし、２つ重なっている部分があるので、見た目は４箇所）から２つの図形を変化させていることが推測できます。

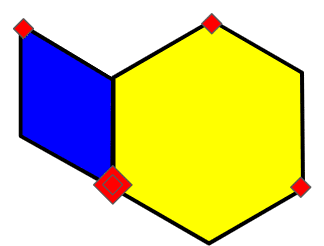
さてそうなると、「HAT」の時点で、回転尾翼の変化する２箇所は「お腹と背中がくっついちゃった状態」となってしまいます。

このさきどうなってるの？って話です。

Tile(1,4)、お前もか！

Tile(1,4)はこんなかたち。

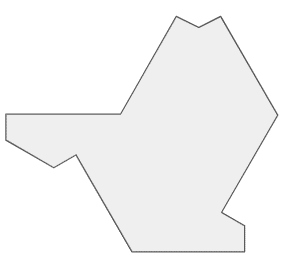
なんというか、猫と鶏のハーフみたいな形状です。
これも、他のタイルと同様に２つの図形にわけてみることにします。
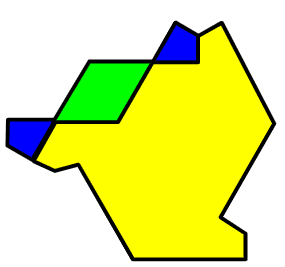
参考に、右に「HAT」を並べてみます。

回転尾翼（青）は離れていますが、点対称にはなっていますが、回転主翼（黄色）は、対称もなにもあったものじゃありません。

しかしですね、Tile(4,1)にある図形（緑）をもう１個追加すると、とんでもないことに気づきます。

そうなのです。
回転尾翼（青＋緑）はつながっていますし、回転主翼（黄色＋緑）は点対称です。
２つの図形が重なっている部分（緑）は、

対消滅で失くなる（ように扱う）

のです！
そうするとですね、もう一方の変化の端にあるTile(0,1)の解釈が変わってきます。

Tile(0,1)は、正三角形を４つ組み合わせた図形ではなく、

正三角形６個組み合わせた図形に、
正三角形２個組み合わせた図形が
重なっているので、
実は正三角形８個組み合わせた図形

ということで、構成する要素はTile(1,0)と同じです。

……ほんまかいな？

【余談】
ちなみに、最初の「HAT」の記事『アインシュタインタイルを愛でる。とにかく愛でてみる。』では、今回の結果とは異なる仮説を立てておりました。

猫の爪は隠れる

Tile(0,1)から変形して、無数の非周期敷詰めモノタイルをたどり、Tile(1,0)に到達します。
さて、Tile(0,1)の変形は、２通りの方向――右利きと左利きみたいなもの――があります。

例えるならば、回転尾翼（青）は猫の爪みたいなものです。
Tile(0,1)からTile(1,0)への変遷は、爪を引っ込める動きが最後まで追えます。
ところが、Tile(1,0)からTile(0,1)は、初っ端で、右？左？どっちの手（脚？）なのか不確定です。

三層に重なる敷き詰め

さらにさらに。
Tile(1,0)は、平面敷き詰めすると、緑の図形は他のTile(1,0)と重なることになるので、都合三層に重なっています。

上の図のように、黄色Tile(1,0)には、緑の部分（見えません）が重なっていて、その上に青Tile(1,0)がさらに重なっています。
青Tile(1,0)にも、緑の部分（見えません）はあります。

この点をふまえて、Tile(4,1)を平面に敷き詰めてみると、

Tile(4,1)の外にある緑の図形（みえません）は、Tile(4,1)内にある２箇所の水色の図形に重なることがあります。

辺の長さを揃えてみる

Tile(4,1)の辺の長さですが、実はあまりきれいではありません。

回転尾翼（青と緑）の辺の長さの比をあらわしてみると、

青の短い辺：青の長い辺：緑の辺＝１：$${\sqrt{3}}$$：４−$${\sqrt{3}}$$

です。
有理数（整数）ー無理数は、計算が面倒くさくなります。

なので、青の長い辺：緑の辺＝１：１にした、別のアインシュタインタイルをこしらえてみます。
１番のメリットは、「HAT」や「TURTLE」のように、凧（Kite）の図形１種類のみの組み合わせで作れるのです。

せっかくなので、もう一方のアインシュタインタイルも作ってみました。
辺の比を考慮すると、左のタイルがTile($${3\sqrt{3},1}$$)で、右のタイルがTile($${1,3\sqrt{3}}$$)となります。

Tile($${3\sqrt{3},1}$$)の凧の数：
３８個（回転主翼：回転尾翼＝３６：２）

Tile($${1,3\sqrt{3}}$$)の凧の数：
６４個（回転主翼：回転尾翼＝４２：２２）

締め

ということで、なんかえらいことになりました。
アインシュタインタイルを愛でて、結局６回も記事を書いてしまいましたが、ひとまず一区切りとします。
また何かあれば、書くかもしれません。

そろそろ、せまゲーの方にも戻っておきたい。

では。