
アインシュタインタイルをもう1個愛でる。とにかく愛でてみる
前回の記事はこちら。
今回は、その続きみたいなものになります。
論文に描かれたもう1個のタイル
非周期的モノタイル「HAT」についての論文「An aperiodic monotile」。
もう1個異なるタイルについても触れられています。
第6章「A family of aperiodic monotiles(非周期モノタイルの仲間)」に描かれているそのタイルがこちら。

https://doi.org/10.48550/arXiv.2303.10798
「HAT」は凧形の四角形を8個組み合わせた形状ですが、上の図形――「TURTLE(亀)」とも呼ばれます――は凧形10個の組み合わせです。

前回の記事で、「HAT」は2つの異なる点対称の図形を組み合わせた形でもある、と書きました。
その特徴を踏まえて「ヘリコプター」と例えてみたりします。

黄色は、凧形6個の組み合わせ。
「TURTLE」もよくよく見ると、これも2つの異なる点対称の図形が組み合わさった「ヘリコプター」でした。
このことについて、日本テセレーションデザイン協会の代表でもある数学者の荒木義明さんのツイートがあります。
こんなヘリコプターどうでしょう。
— Yoshiaki Araki 荒木義明 (@alytile) April 25, 2023
5-Gem(Turtle)のパラメータでも線対称と3回対称の図形に分割できるのが面白いですね pic.twitter.com/3PmFgxNzyY
「HAT」と「TURTLE」の回転主翼(黄色の図形)の向きを合わせて並べてみます。

回転尾翼(青色の図形)の位置の違いが興味深いです。
まだまだ似ていました
荒木さんのツイートの画像に登場した「Aperodic Tile Maker」ですが、「HAT」を元にして、
・面積を変えない
・各辺の長さを一定の割合で変化させる
このルールで、様々な形状のタイルを描いています。
つまり、「HAT」を変形すると「TURTLE」になります。
で、「TURTLE」をしばらく眺めていると、前回の記事で書いたことがよぎりました。

https://doi.org/10.48550/arXiv.2303.10798
「HAT」を形作る2つの長さの辺のうち、同じ長さの辺を平行移動すると、2つの異なる図形を作ることができます。

※黒い辺の長さを1とすると、オレンジの辺の長さは$${\sqrt{3}}$$です。
これと同じことを「TURTLE」でやってみると、どうなるのか?
「HAT」との比較のため、「TURTLE」を少し回転していますが、結果はこちら。
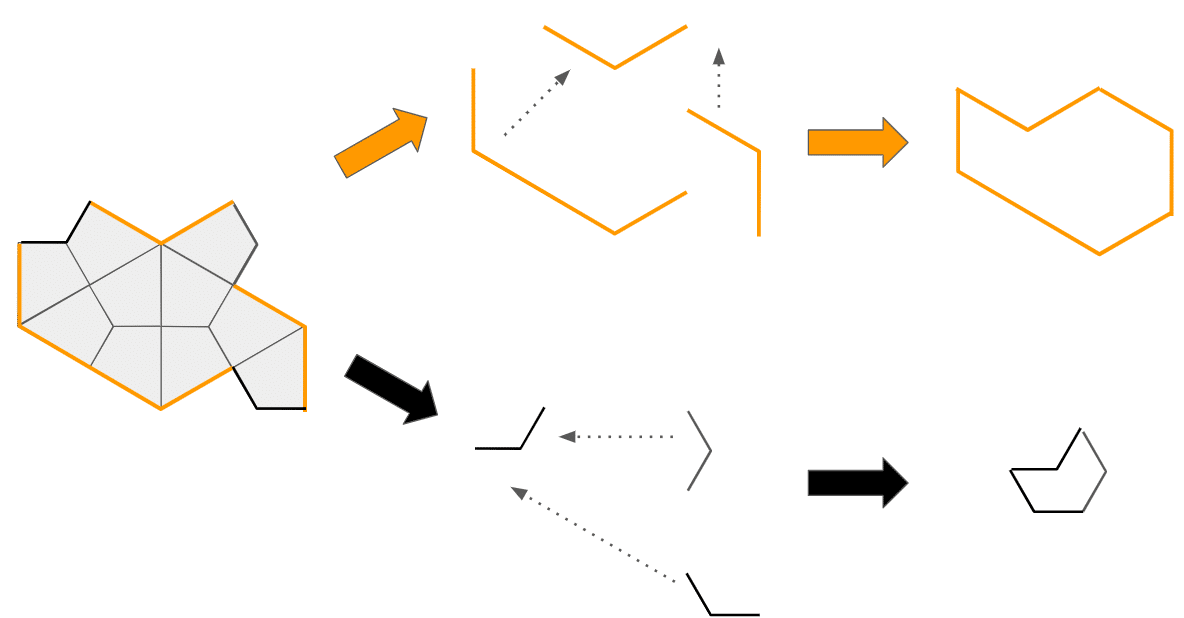
ええええ?!
同じ2つの図形が、しかも辺の長さが入れ替わって、つくれました。
締め
ということで、もう1個の図形「TURTLE」を愛でてみました。
もうちょっと愛でるかも知れません。
では。
