「プログラマ脳を鍛える数学パズル」を解いてみる中級編#3【アルゴリズム学習】

概要

翔泳社から出版されている「プログラマ脳を鍛える数学パズル」のプログラミング問題をC++で解きます。
この本ではRuby,JavaScript,Cでの解答はありますが、C++は載っていないため練習として解いてみようと思います。
note、コード共にまだまだな部分も多いので、何かお気づきの点があれば、コメントお願いいたします。

入門編はコチラ
初級編はコチラ

ぜひ、いいねと思ったらスキお願いいたします！！！
見出し画像は最近食べたおいしいものです。

問題１

Q35：運命の出会いは何通り？

解答１

ソースコード

#include <bits/stdc++.h>
using namespace std;
#define rep(i, n) for(int i = 0; i < (int)(n); i++)
#define all(x) (x).begin(),(x).end()
#define repi(i,a,n) for(int i = (int)a; i < (int)(n); i++)
#define ll long long

int N=6;
//二人の位置から出会っているか判定、その後移動させ再検索
//manX,manYは男性の位置、womanXとwomanYは女性の位置、meetは出会った回数
ll int search(int manX,int manY,int womanX,int womanY,int meet){
   ll int cnt=0;
   if(manX <= N && manY <= N && womanX >= 0 && womanY >=0){//移動が完了していないとき
       if(manX == N && manY == N && meet >= 2)cnt++;   //男が端に到着して、出会った回数が2回以上
       if(manX == womanX)meet++;
       if(manY == womanY)meet++;
       //最短距離を進むので、移動方法は4通り
       cnt+=search(manX+1,manY,womanX-1,womanY,meet);//男が上、女が下に移動
       cnt+=search(manX+1,manY,womanX,womanY-1,meet);//男が上、女が横に移動
       cnt+=search(manX,manY+1,womanX-1,womanY,meet);//男が横、女が下に移動
       cnt+=search(manX,manY+1,womanX,womanY-1,meet);//男が横、女が横に移動
   }
   return cnt;
}
int main(void){
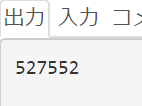
   std::cout << search(0,0,N,N,0) << std::endl;
   
}

実行結果

問題２

Q36：「0」と「7」の回文数

解答２

ソースコード

#include <bits/stdc++.h>
using namespace std;
#define rep(i, n) for(int i = 0; i < (int)(n); i++)
#define all(x) (x).begin(),(x).end()
#define repi(i,a,n) for(int i = (int)a; i < (int)(n); i++)
#define ll long long

int main(void){
   std::vector<int> ans;
   //nをループ
   repi(i,1,51){
       int j=1;
       //「0と7の数字」を2進数を1ずつ増やすことで検索
       while(true){
           bitset<64> tmp(j);//2進数の作成
           string t_string=tmp.to_string();
           int num=std::atoi(t_string.c_str());
           
           num*=7;//7をかけることで0と7の数字を実現
           
           if(num%i==0){
               //回文を作成
               string a=to_string(num);
               string rNum=a;
               reverse(all(rNum));
               
               if(a==rNum && (i%2!=0 || i%5!=0)){//条件に当てはまる場合
                   if(a.find("0") != std::string::npos){//0を含む場合
                       std::cout << i <<":"<< i <<"*"<< num/i <<"="<< a << std::endl;
                   }
               }
               break;
           }
           j++;
       }
   }
}

実行結果

0と７が両方ある場合

0を含まない可能性も考える場合

今回の学び

・q35は最短距離をすすむという条件だったため、簡単に実装できた。
移動範囲が正方形じゃなくなったらもっと難しくなるかも（問題の定義も難しくなるが）。

・q36は2進数を64ビットで表すことで実装したが、64ビット使うことはすくないため、ほとんどの場合メモリの無駄になっていると思う。

・q36について、私の実装方法では、2進数を毎回計算しているため、処理量が多い（メモ化すれば多少はましにはなる）。本通りに逆で実装した方が、処理量は少なかった。その場合、２進数をwhileで割り続けて求める方法にすれば、64bitのbitsetを使わなくて済む。

参考文献

「プログラマを鍛える数学パズル」著:増井敏克

プログラマ脳を鍛える数学パズル シンプルで高速なコードが書けるようになる70問