
コミットメントスキーム
今回は、ZK-SNARKの構成要素である「関数を用いたコミットメントスキーム」と「適切なIOP(Interactive Oracle Proof)」のうち、「関数を用いたコミットメントスキーム」について見ていきます。
コミットメントとは
暗号技術としてのコミットメントのイメージは、「封筒」です。差出人がdataを封筒に入れ、受取人は中身を見るために封筒を開けます。この「封筒に入れる」と「封筒を開ける」に相当するものが、$${commit}$$と$${verify}$$です。

① コミット:$${commit(m,r) \to com}$$
コミットでは、ランダムに選んだ値$${r}$$とともに、メッセージ$${m}$$に対して$${com}$$を生成します。
また、生成した$${com}$$からはメッセージの中身について何も漏れることがありません。このように、検証者が証明者から$${m}$$を受け取るまでは、$${m}$$は秘匿化されるという性質を秘匿性(Hiding)と呼びます。
② 検証:$${verify(m, com, r) \to accept or reject}$$
検証では、証明者から渡された$${r}$$とメッセージ$${m}$$から$${com'}$$を生成し、コミットメント$${com}$$と比較することで、メッセージ$${m}$$が一貫していることを確かめます。
・$${com = com'}$$の場合
正しくコミットメントが生成されており、証明者は正しいメッセージ$${m}$$に対してコミットしたと判断します。
・$${com \ne com'}$$の場合
証明者が不正を行った or 誤ったメッセージを開示した(コミット後にメッセージを変更した)と判断します。このように、1つのコミットメントから2つの異なる解は導かれないため、一度コミットメントが生成されると、後から別のメッセージを正当化することができません。このような性質を束縛性(Biding)と呼びます。
ハッシュ関数を用いたコミットメントの構築
先ほどのコミットメントの説明では、$${commit(m,r)}$$として使用する関数を$${commit}$$と仮置きしていました。関数にハッシュ関数$${H}$$を使用する場合、メッセージ$${m}$$とランダム値$${r}$$の2つの入力に対してハッシュ値を出力します。したがって、以下のように書くことができます。
$${H: {\mathcal M} \times {\mathcal R} \to C}$$に対して
① コミット:$${com := H(m,r)}$$
② 検証:$${accept if com = H(m,r)}$$
関数へのコミットメント
ハッシュ関数を用いたコミットメントでは、$${m}$$という値をハッシュ関数でコミットメントしました。一方、具体的な値ではなく、関数全体に対してコミットする方法もあります。ここでは、関数へのコミットメントについて見ていきます。
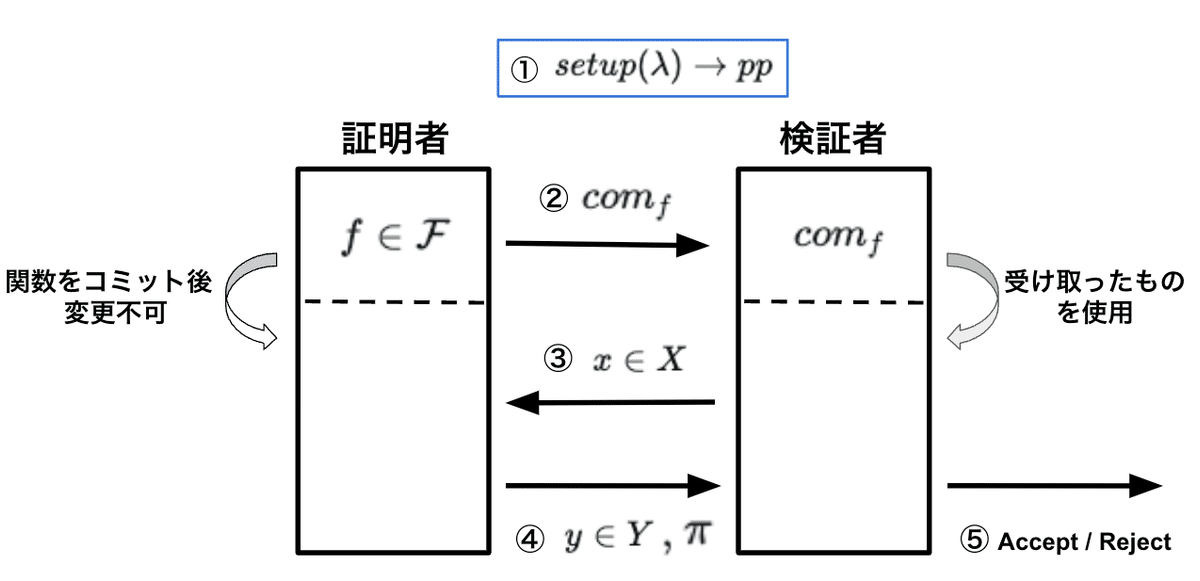
① 公開パラメータの生成:$${setup(\lambda) \to pp}$$
公開パラメータを生成します。この時使用する$${\lambda}$$は、セキュリティの強度を制御するためのセキュリティパラメータで、128や256が代入される場合が多いです。
② コミットメント$${com_f}$$の生成:$${commit(pp, f, r) \to com_f}$$
証明者は、
・①で生成した公開パラメータ
・選択した関数$${f \in {\mathcal F}}$$
・ランダム値$${r \in R}$$
からコミットメント$${com_f}$$を生成します。
③ 検証者から証明者に、$${x}$$を渡す
④ 証明$${\pi}$$の生成:$${P(pp, f, x, y, r) \to \pi}$$
証明者は、
・①で生成した公開パラメータ
・選択した関数$${f \in {\mathcal F}}$$
・③で受け取った$${x}$$
・$${y=f(x)}$$を満たす$${y}$$
・ランダム値$${r \in R}$$
から証明$${\pi}$$を生成します。
⑤ 受理 or 拒否:$${V(pp, com_f, x, y, \pi) \to accept or reject}$$
検証者は、
・①で生成した公開パラメータ
・⓶で受け取った$${com_f}$$
・③で受け取った$${x}$$
・$${y=f(x)}$$を満たす$${y}$$
・④で受け取った$${\pi}$$
から、受理 or 拒否します。
コミットメントを生成する際のインプットとして関数を使用していますが、
ここからは代表的な関数を使用するコミットメントについて見ていきます。
① 多項式コミットメント(Polynomial Commitments)
コミットメントする関数は、$${{\mathbb F}_p^{(\le d)}[X]}$$です。
(ex. $${f(x) = a_nX^d+a_{d-1}X^{d-1}+…+a_1x+a_0}$$)
② 多重線形コミットメント(Multilinear Commitments)
コミットメントする関数は、$${{\mathbb F}_p^{(\le 1)}[X_1, X_2, …, X_k]}$$です。
(ex. $${f(x_1, …, x_k)=x_1x_3+x_1x_3x_5+…}$$)
③ 線形コミットメント(Linear Commitments)
コミットメントする関数は、$${f_{\vec v}(\vec u) = <{\vec u}, {\vec v}>={\sum_{1\le k\le n}}u_iv_i}$$です。
以下は、①~③で使用する関数を整理した図になります。

上図にあるように、線形コミットメントをより一般化したものが多重線形コミットメントであり、多重線形コミットメントを一般化したものが多項式コミットメントです。つまり、多項式コミットメントが最も汎用的であることがわかります。
最後に
今回は、コミットメントについて確認しました。特に、値をコミットするのではなく、関数をコミットするという部分がポイントでした。次回は、最後に登場した「多項式コミットメント」について見ていきます。ぜひチェックしてください!
[参照]
この記事は、『ZK Hack Whiteboard Session1 Module2: Building a SNARK, pt1 by Dan Boneh』の動画の内容を編集し、図や説明を加えたものです。
ZK Hackとは、ZKに関するビデオやニュースレターの発信や、イベントを開催するコミュニティです。今回のビデオは、Stanford大学のDan Boneh教授によるSNARKの入門動画になります。
