
PLONK
今回は、ZK-SNARKの構成要素である「適切なIOP(Interactive Oracle Proof)」のうち、「PLONK」と呼ばれるプロトコルについて確認していきます。
回路のコンパイル
計算過程の整理
PLONKでは、回路での計算の正当性を後から検証する用に、計算過程を記録していきます。
例として、$${(x_1+x_2)(x_2+w_1)}$$を算術回路として表現する際に、どのように計算過程を記録するかをみていきます。

まずはこれまでの記事でも確認した通り、対象の式を要素に分解し、算術回路を作成します。そして過程の整理では、ゲートに着目し、ゲートに対して左からの入力値、右からの入力値、ゲートの出力の3つを記載していきます。
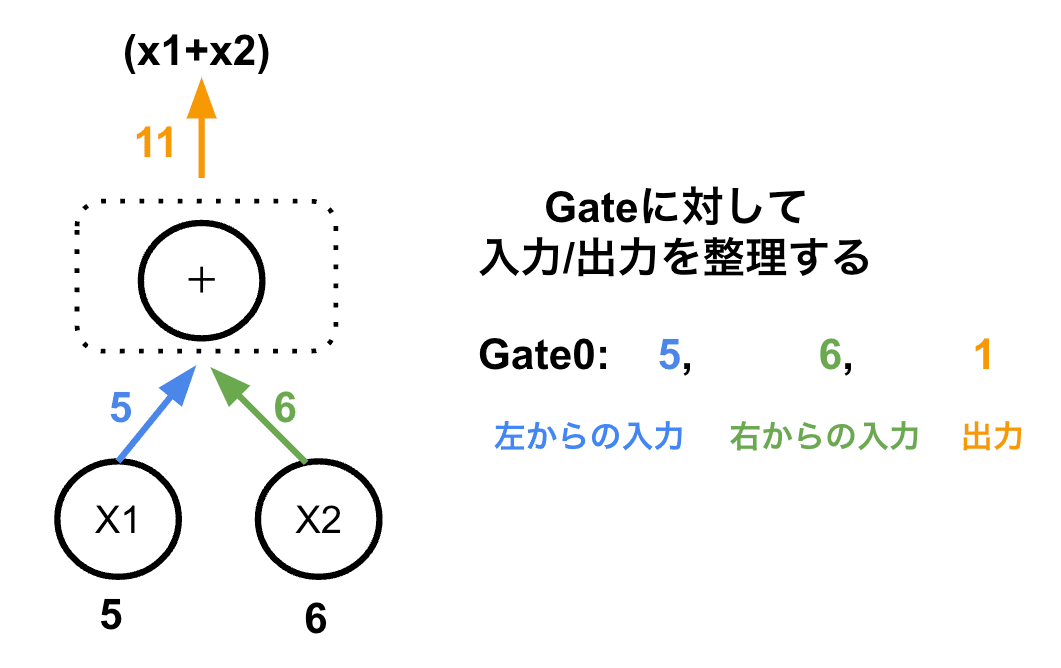
これをすべてのゲートに対して行い、算術回路の計算過程を整理します。
多項式での表現
次に、上記で整理したものを多項式で表現することで、計算全体をエンコードします。
まず、ゲートの数を$${|C|}$$、入力の総数を$${|I|}$$、回路のサイズを表す指標として$${d}$$、有限群$${H}$$を以下のように定義します。
・$${|C| := }$$回路Cに含まれるゲートの総数
・$${|I| := |I_x|+|I_w|=}$$回路Cに対する入力の総数
・$${d := 3|C|+|I|}$$
・$${H = \{1,w,w^2,…,w^{d-1}\}}$$
次に、回路内の計算過程を整理したものを、以下のように多項式で表現すると仮定します。


これに則り、最初に整理した表を多項式で置換すると以下のようになります。

このようにして、計算過程を多項式で整理することができます。
コミットメントの妥当性の証明
ここまで確認したプロセスについて、全ての計算過程が正しく処理されているかを証明する必要があります。
具体的には、以下の4つを証明します。
(1) 入力値のエンコード
(2) ゲートでの計算
(3) ワイヤリング
(4) 最後のゲート出力が0である
(1) 入力値のエンコード
ここでは、回路の入力値が正しくエンコードされていることを証明します。証明者と検証者は、回路の入力値をエンコードする多項式$${v(X) \in {\mathbb F}_p^{\le |I_x|}[X]}$$を作成し、回路の入力値が正しくコンパイルされているかを確認します。

この式は、$${P(y)-v(y)}$$という多項式がある有限体$${H_{inp}}$$上のすべての点で0となると読み替えることができるため、前回登場した「ゼロテスト」を行うことで$${P(X)}$$が正しく入力をエンコードしていることが確認できます。
(2) ゲートでの計算
ここでは、各ゲートでの計算が正しく行われていることを証明します。
まず、セレクター多項式$${S(X) \in {\mathbb F}_p^{\le d}[X]}$$を用いて、各ゲートが加算か乗算かを表現します。

次に、これらを用いて証明者は以下の式を計算することでゲートでの計算の正しさを証明します。

先ほどと同様に「ゼロテスト」を行うことで、各ゲートにおいて正しく計算がされていることが確認できます。
(3) ワイヤリング
ここまで計算過程を整理してきましたが、ゲートに着目すると「前の段のゲートの出力」が「次の段のゲートの入力」になっていることがわかります。ここでは、この制約が成立していることを証明します。
(1)の具体例で確認すると、以下のように立式できます。

ここで、値を回転させるような多項式$${W: H \to H}$$を定義します。
$${W(w^{-2}, w^1,w^3)=(w^1,w^3,w^{-2})}$$
$${W(w^{-1},w^0)=(w^0, w^{-1})}$$
これを用いると、ワイヤリングの証明は以下のように帰着できることがわかります。

ただし、この多項式$${W:H\to H}$$は次数が$${d^2}$$になってしまい、証明にかかる計算量が2次時間になってしまいます。($${d}$$ : 有限群$${H}$$の位数)
そこで、新しい関数$${L(Y,Z)}$$を導入し、前回登場した「積の確認(Prod-check)」を使用することで、線形時間での証明が実現します。

ここで登場する$${L_1(X)}$$と見てみると、分母と分子の違いは
分母:$${y・W(x)}$$
分子:$${y・x}$$
の部分であることがわかります。これは先ほど出てきた
$${P(y)-P(W(y))=0}$$ …(*)
を徐算に落とし込むことで次数$${d}$$での計算に帰着させ、(*)が成立するときには商が1となることを確かめるためにProd-checkを使用しています。


(4) 最後のゲート出力が0である
これは主に(多項式)=0の形に帰着させることが多いため、最後のゲートの出力が0であることを以下の式で確かめます。
$${P(w^{3|C|-1}=0}$$
このように、(1)~(4)を全て証明することで、算術回路が正しくコンパイルされていることが保証されます。
最後に
今回は、PLONKにおける算術回路のコンパイル過程について見てきました。前回確認したSum-checkやProd-checkが実際に使用されていたり、多項式を用いて表現した入力/出力を用いて証明するポイントでした。次回は、ここまで触れたPLONKで実際にどのような計算が行われているかを手計算で確認するので、ぜひチェックしてください!
[参照]
この記事は、『ZK Hack Whiteboard Session1 Module3: Building a SNARK, pt2 by Dan Boneh』の動画をベースに、図や説明を加えたものです。
ZK Hackとは、ZKに関するビデオやニュースレターの発信や、イベントを開催するコミュニティです。今回のビデオは、Stanford大学のDan Boneh教授によるSNARKの入門動画になります。
