
算術回路
今回は、SNARKの基本となる「算術回路」についてみていきます。
SNARKの簡単な説明
SNARKとは、Succinct Non-Interactive Argument of Knowledgeの頭文字をとったもので、ある命題(statement)が真であることを簡潔(succinct)に示すための非対話型証明プロトコルを指します。簡潔な証明というのは、短く、すぐに検証できることを指します。命題の例を挙げると、ある関数f(x)に対して
"$${f(m)=0}$$となるようなmを知っている"
というものです。
SNARKは、主に以下の5つのステップに分解できます。
1. 計算問題の定式化する (ある命題が真であるかを、与えられたにゅ力に対して特定の条件を満たすかどうかに読み替えたもの)
2. 上記の計算問題を、算術回路に変換する
3. 上記の算術回路を、二次方程式プログラム(Quadratic Arithmetic Program)に変換する
4. 証明者が、入力/算術回路/QAPを用いて証明を生成する
5. 検証者が、上記の証明と公開情報を用いて検証する
この中で2に登場する、算術回路について見ていきます。
算術回路とは
算術回路とは、ある計算問題をグラフに落とし込んだものです。
具体例で確認します。はじめに、3以上の素数pに対して、
$${F=0,1,2,…,p-1}$$
という有限群を用意します。
<確認>
素数:その数値と1以外に整数の約数が存在しないもの(3,5,7,11など)
有限群:ある条件を満たすような、有限個の要素からなる集まり
(数学編で詳しく触れます)
また対象の計算式を、$${x_1(x_1+x_2+1)(x_2-1)}$$とします。
それでは、この計算問題をグラフに変換する各ステップを見ていきます。
【登場する変数/数値の整理】
まずは、数式に登場する数値の種類を整理します。
この例では、$${x_1, x_2, 1}$$の3種類なので、グラフの一番下の段に入力します。
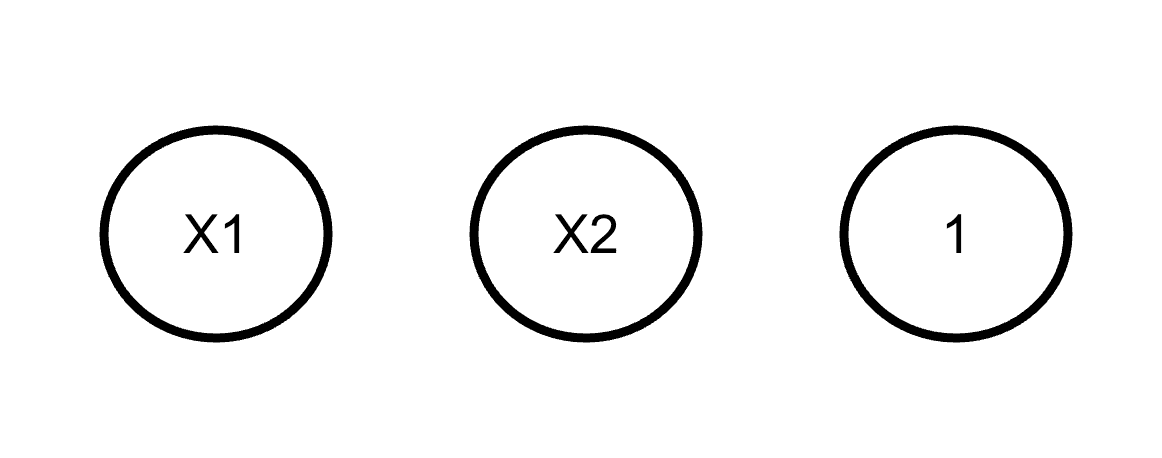
【かたまりに分解】
次に、計算式をかたまりに分解します。
$${x_1(x_1+x_2+1)(x_2-1)}$$は、以下の3つの要素に分解することができます。
・$${x_1+x_2+1}$$ …これをaとします
・$${x_2-1}$$ …これをbとします
・$${x_1 \times a \times b}$$
【かたまりを1つずつ再現】
$${a, b, x_1 \times a \times b}$$を、グラフの下段に入力した数値で再現していきます。
まずaを作成するため、入力値の1つ上段のゲートに+をラベルし、入力値と繋ぎます。(+/-/×をラベルするものをゲートと呼びます)
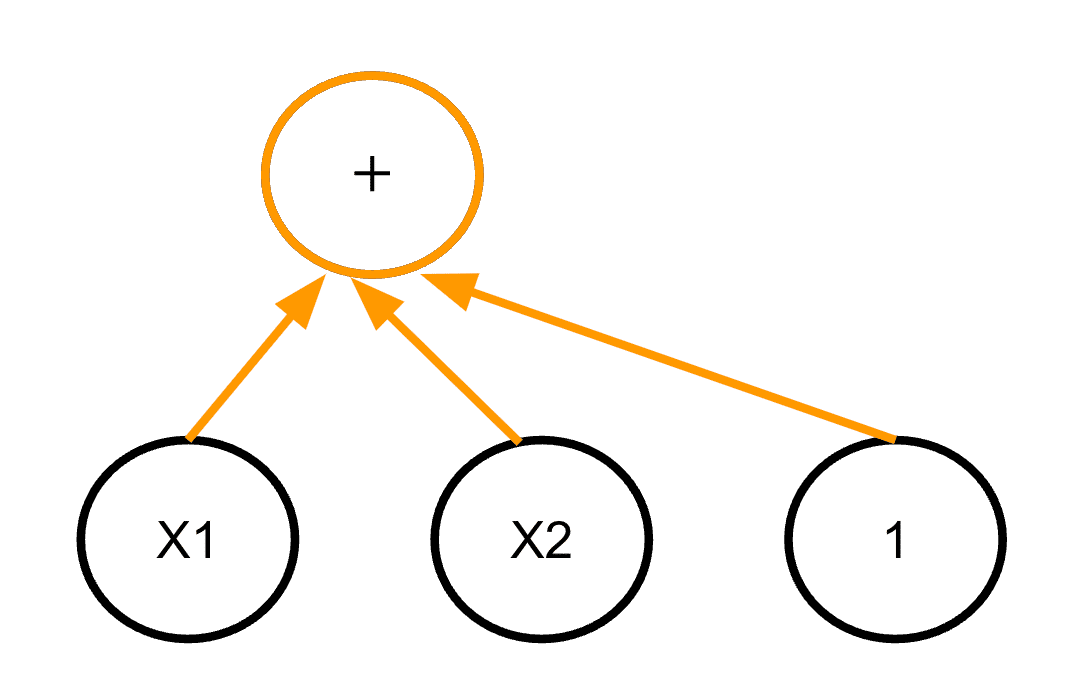
次にbを作成するため、同様にゲートに-をラベルし、入力値と繋ぎます。

aとbを作成したグラフを合わせます。

最後に$${x_1 \times a \times b}$$を作成するため、最上段のゲートに×をラベルし、$${x_1}$$、a、bと繋ぎます。

$${x_1(x_1+x_2+1)(x_2-1)}$$を作成したので、出力します。

有限体$${F}$$上の3つの入力に対して1つを出力するので、この算術回路Cは
$${C : F^n\to F}$$
となります。
また算術回路のサイズの指標として、
|C|=(ゲートの数)
があります。
この例では+/-/×の3つのゲートがあるため、|C|=3となります。
最後に
今回は、ZK Hack Module1で登場する算術回路について、どのように回路を生成していくのかを見てきました。使用した演算子に除法(÷)が登場しなかったことに気付いた方がいるかもしれません。実はZKでは、加算(+)、減算(-)、乗算(×)で計算式を表しますが、これは有限体上における計算方法に関連するものです。この辺りも数学編で触れていくので、次回以降もぜひチェックしてください!!
[参照]
この記事は、『ZK Hack Whiteboard Session1 Module1: What is a SNARK?』の動画の内容を編集し、図や説明を加えたものです。
ZK Hackとは、ZKに関するビデオやニュースレターの発信や、イベントを開催するコミュニティです。今回のビデオは、Stanford大学のDan Boneh教授によるSNARKの入門動画になります。
