Pythonでコンビニの売上を時系列分析をしてみる~もしコロナがなかったら~

はじめに

Aidemy Premiumにて「データ分析コース」を３ヶ月受講。

数あるプログラミングの中で、データ分析、機械学習、Pythonに一番興味を持ちました。これらのプログラミングを学びそれを活かして仕事・キャリアアップをしていきたいと思いAidemy Premiumを受講しています。
知識定着のためにこの記事を書いています。わかりにくい点もあると思いますが、知識や経験を共有できるように記述していきます。

学んだ時系列分析、データの予測をコンビニのデータを使ってトライして見ます。

実行環境
Google Colaboratory
python　3.8.5

使用するライブラリ

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import itertools

分析対象
日本のコンビニ売上のデータセットを使用し、月間売上のデータを予測します。
経済産業省の時系列データ『コンビニエンスストア商品別販売額』
からコンビニの月間売上のデータを取得します。
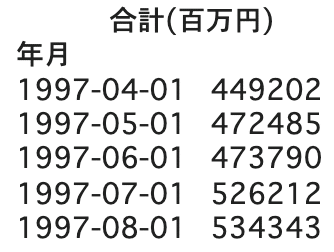
下記のようなデータで先頭から５行のみ表示させていますが、
1997年4月〜2021年9月までのデータとなります。

そもそも時系列分析とは何？

過去のデータを分析し、未来を予測することです。
会社や商品の売上予測、来店者数の予測など、ビジネスにおいて重要な分析技術です。
時系列分析の第一歩は、時系列データを 視覚化することです。データをグラフにすることで様々なことがわかります。

時系列データには 3つのパターンがあります。

トレンド
データの長期的な傾向を意味します。時間の経過とともにデータの値が上昇していたり下降していたりする時系列データは「トレンドがある」といい、値が上昇している場合には 正のトレンド 、下降している場合には 負のトレンド があると言います。

周期変動
周期変動があるデータは時間の経過に伴ってデータの値が上昇と下降を繰り返します。特に1年間での周期変動を 季節変動 といいます。

不規則変動
不規則変動は時間の経過と関係なくデータの値が変動することをいいます。実際の時系列データを観測すると、トレンド、周期変動、不規則変動が組み合わさっていることが分かります。 

この３つのパターンを念頭に、
今回分析で使用するコンビニのデータをグラフで視覚化させます。

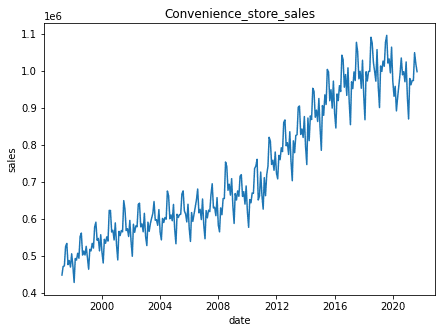
データの上がり下がりがある周期変動の特徴と右肩上がりのトレンドが見て取れますね。

下記コード

df = pd.read_csv('/content/コンビニ売上２.csv', encoding='utf-8')
df = df[['年月','合計']]#カラムの指定
df["年月"] = pd.to_datetime(df["年月"], format='%Y年%m月')#日付の整理
index = df["年月"]
df.index = index
df2 = df.drop(columns=["年月"])
base_df = df2.rename(columns={'合計': '合計(百万円)'})
print(base_df)

plt.figure(figsize=(7, 5))
plt.plot(base_df)
plt.title("Convenience_store_sales")
plt.xlabel("date")
plt.ylabel("sales")
plt.show()

上記のデータを使って、時系列データが持っている様々な特徴を説明できるようなモデルを構築 します。モデルとは「入力→モデル→出力」というコンピューターが受け取った入力データから、モデルが具体的な評価・判定を行い、出力するというものです。そのモデルを使用して、様々な予測を行ったり、相互の関連を分析していきます。

モデル構築・分析の前に
必要な用語、考え方をいくつか紹介します。

時系列分析をより理解するための用語集

1. 原系列
2. 自己相関、偏自己相関
3. 定常性
4. 対数系列
5. 階差系列
6. ホワイトノイズ
7. 季節調整の利用

1.原系列
なにもされていない時系列データそのものは 原系列と呼ばれます。
時系列分析において 原系列 そのものを扱うことはあまりありません。
実際には時系列データを加工し新しい系列にして、それを分析して モデル を構築していきます。

2.自己相関係数（ACF:Autocorrelation Function）　
    偏自己相関係数（PACF, partial autocorrelation function）

自己相関とは、
自己の過去のデータとの相関のこと。過去の値とどれほど似ているのか、過去の値が現在のデータにどれくらい影響しているかを現した値のことです。
下記のグラフのように自己相関を可視化したものはコレログラフと呼ばれます。今回のデータではコレログラムを書かなくても周期性があるということはわかりますが、未知のデータでさらにデータのばらつきが大きい場合に、時系列データをみただけでは周期性があるかどうかは判断が困難です。そんなときにコレログラムでみてあげると、客観的に周期性の相関がみえてきます。

以下、今回のデータの自己相関のコレログラフ

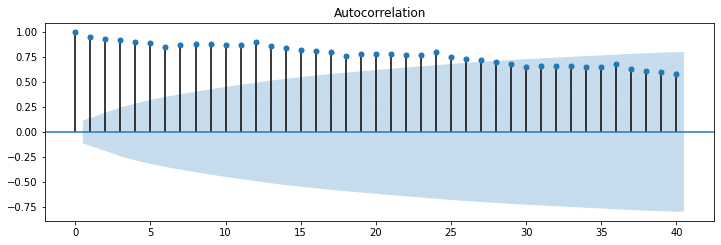
このグラフを見ると、12で少し高い値となっています。そして、この傾向が13以降も繰り返されているのがわかります。
12, 24, 36で少し高い値となっているということは、これは12か月の周期性（季節性）があるということを表しています。

偏自己相関とは、
自己相関同様、過去のデータとの相関のことです。
過去の値とどれほど似ているのか（相関があるのか）を表す指標ですが、自己相関係数とはちょっと違います。

例えば、7日間前のデータとの自己相関係数を求めると、ある日のデータが前日のデータと相関があった場合、7日前→6日前→5日前......1日前→今日とデータを通して相関している可能性があります。
一方、偏自己相関係数の場合は、６日前〜１日前のデータの影響を取り除き、ある日のデータと７日前のデータをピンポイントで相関を求めることができます。間の影響を受けないピンポイント自己相関係数みたいなイメージです。

以下、今回のデータの偏自己相関のコレログラフ

青色の影は95%信頼区間です。
この点線の中におさまっていれば自己相関を持たない、つまり現在の自分と過去の自分は関係ないということです。
95%信頼区間領域を超えているラグのデータが影響を与えていることがわかります。

以下、自己相関、偏自己相関のコレログラフのコード

base_df_acf = sm.tsa.stattools.acf(base_df, nlags=40,fft = False)
print(base_df_acf)

fig=plt.figure(figsize=(12, 8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(base_df, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(base_df, lags=40, ax=ax2)
plt.show()

3.定常性

時間の経過によらず一定の値を軸に変動しており(期待値が一定)、
一定の値を軸に同程度の幅で振れて変化する(データのばらつきが一定＝自己共分散が一定)

この時系列データを定常性のあるデータと言います。
なぜ 定常性 が重要なのか？
時系列データにおいて定常性がないデータを分析した結果、全く意味のない相関を検出してしまう可能性があるからです。時系列データとは時間の経過に沿って変化するデータなので、「時間の経過」という項目 が無意味な相関関係を生んでしまいます。(擬似相関 )
このような 時系列データの無意味な相関を検出しないため に、定常性のない時系列を定常過程にする方法は、
・対数変換 によって、変動の 分散 を一様にする
・階差系列に変換することでトレンド・季節変動を除去する
・季節調整の利用
・移動平均を取り、季節変動を除去しトレンドを抽出した後、原系列からトレンド成分を除去する
などがあります。
時系列分析は、定常性のあるデータに変換してから分析を進める必要があります。

4.対数系列
原系列を定常性のあるデータに変換する手法の１つ。
時系列データの中には、値の変動が大きなデータが多くあります。そのようなデータの変動を穏やかにするのが 対数変換で、変動の激しい時系列に対して自己共分散を一様にすることができます。

5.階差系列
原系列を定常性のあるデータに変換する手法の１つ。
ひとつ前の値との差をとることを 差分をとる といいます。この様に差分をとった後の系列を 階差系列といいます。
この変換を行うことで原系列の トレンド・季節変動を取り除く ことができます。
トレンドを取り除くことで原系列を 定常過程（時間がたっても全体で見れば、その時系列の値は変わらないという性質のこと）にすることができる。

以下、今回のデータの上段が原系列・下段が階差系列のグラフとコード

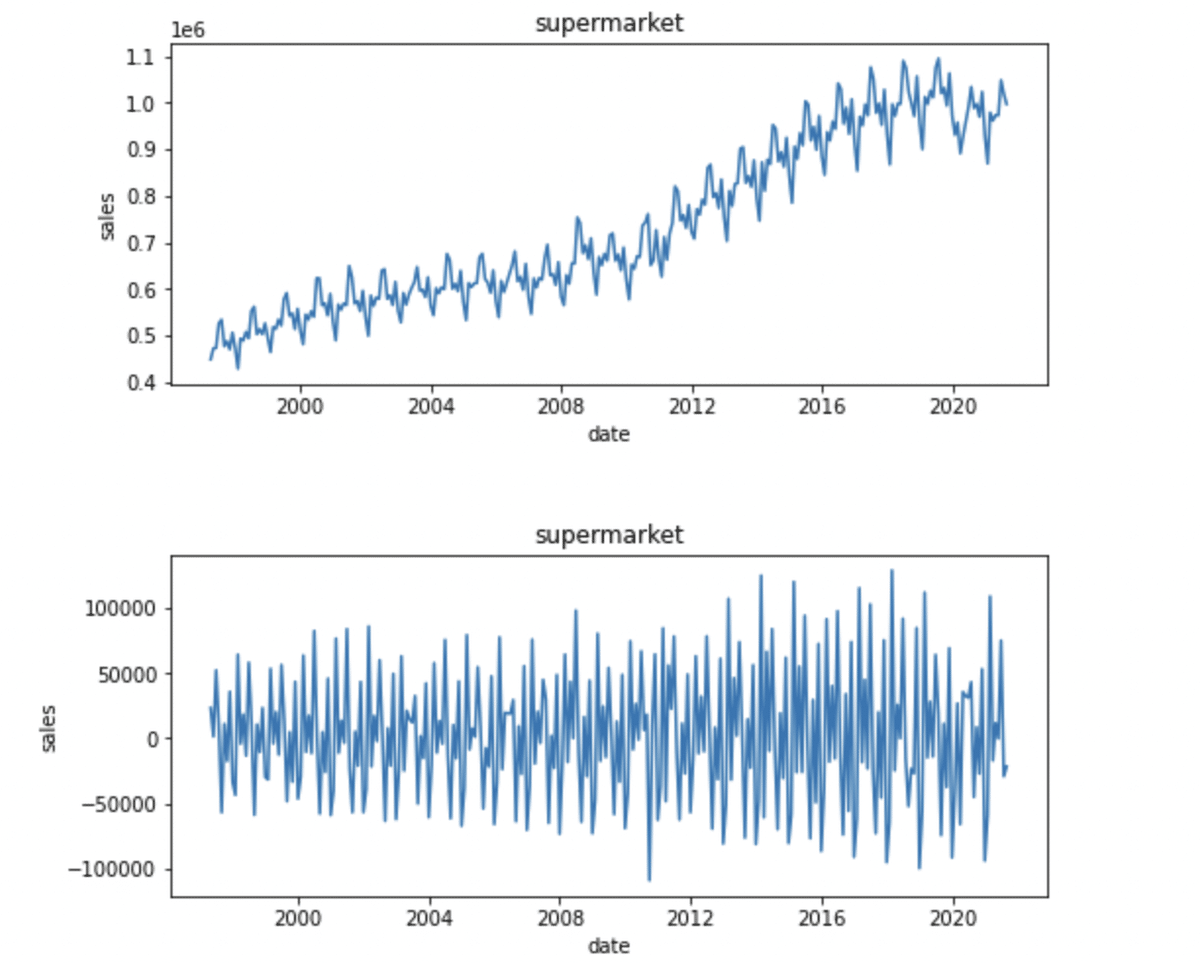
plt.figure(figsize=(8, 8))
plt.subplot(2, 1, 1)
plt.title("supermarket")
plt.xlabel("date")
plt.ylabel("sales")
plt.plot(base_df)
# 階差をとる
plt.subplot(2, 1, 2)
plt.title("supermarket")
plt.xlabel("date")
plt.ylabel("sales")
base_df_diff = base_df.diff()
# 階差系列のプロット
plt.subplots_adjust(wspace=1, hspace=0.5)
plt.plot(base_df_diff)
plt.show()

6.ホワイトノイズ
ホワイトノイズは時系列モデルにおける不規則変動パターン(誤差)を担います。不規則変動自体は数学的な再現が難しいため、ホワイトノイズを用いるのです。これは時系列モデルを作成・検証する上において残差分析のところで必要になります。
ホワイトノイズというのは、以下の３点を満たす時系列のことをいいます。①平均がゼロ
②分散が一定
③自己共分散がゼロ
③の自己共分散とは、自分のデータ(例えば１期前のデータと２期前のデータなど)の間に相関関係がないことを意味です。つまり統計学におけるホワイトノイズとは、事前にどのような値がでてくるかはわからないけれども、ある一定の数値の幅でランダムに変動し、データ全体の平均と分散はゼロとなるような変数であると言えます。

7.季節調整の利用
原系列を定常性のあるデータに変換する手法の１つ。季節変動のあるデータから季節変動以外のデータの動向を探るため、原系列から季節変動を取り除くことが多くあり、そのように季節変動が取り除かれたデータのことを 季節調整済み系列といいます。
原系列 →トレンド + 季節変動 + 残差のデータに分けられます。

以下、今回のデータのグラフとコード

fig = sm.tsa.seasonal_decompose(base_df,freq=12).plot()
plt.show()

原系列 、トレンド 、 季節変動 、 残差の順にデータが分けられてますね。

時系列分析のモデル作成と分析

長くなりましたが、
これから時系列分析を実際に行っていきます。
時系列解析の流れは下記の通りです。

1.データの読み込み
2.データの整理
3.データの可視化
4.モデルの決定
5.パラメーターの決定
6.s以外のパラメーターの決定
7.モデルの構築
8.SARIMAモデルの実行・データの予測とその可視化
すでに３.までは完了しているので、
４.のモデルを決定していきます。

4.モデルの決定

モデルにはいくつかあり、
ARモデル
ARモデル(自己回帰モデル)は規則的に値が変化していくモデルです。
過去の値から回帰的にある時点の値を推定するモデルとなっています。

MAモデル
このMAモデルは、過去の誤差に影響されるモデル。
移動平均モデルとも呼ばれています。
移動平均とは時系列データのある一定の区間で”平均”をとる、ということを区間を”移動”させながら繰り返すことです。こうすることで、元のデータの特徴を残しつつ、データを滑らかにすることができます。
単に時系列が異なる式との間に共通部分を持つために相関性が存在するという性質を持つモデルです。

ARMAモデル
ARモデル、MAモデルを組み合わせて定式化したモデル。AR(p)のARモデルとMA(q)のMAモデルを組み合わせたときARMA(p,q)のように表すことができます。

ARIMAモデル
先程のARMAモデルへ原系列を階差系列に変換し適応したものをARIMAモデルと言います。ARMAモデルは定常過程にしか適応できませんがARIMAモデルは非定常過程（データの平均や分散が時間に依存している過程）にも適応可能です。
d時点前との差分をとった場合のARMA(p,q)で構築したARIMAモデルをARIMA(p,d,q)と表します。
 このARIMAモデルにおける
　・ppを自己相関度
   　モデルが直前 pp 個の値を用いて予測されること
　・ddを誘導 
    　時系列データを定常にするために dd 次の階差が必要だったこと 
　・qqを 移動平均
    　モデルが直前 qq 個の値に影響を受けること 
と呼びます。

SARIMAモデル
 SARIMAモデル とはARIMAモデルをさらに季節周期を持つ時系列データにも拡張できるようにしたモデルです。SARIMAモデルは(p, d, q)のパラメーターに加えて(sp, sd, sq, s)というパラメーターも持ちます。
sp:季節性自己相関
sd:季節性導出,
sq: 季節性移動平均

sp,sd,sq の場合、現在のデータはひとつ以上の季節期間を経た過去のデータに影響されます。
s のパラメーターは周期を表し、sq=1 ならちょうど12ヶ月(1周期前)のデータ, sq=2sq=2 なら12ヶ月前のデータと24ヶ月前のデータの影響をモデルが受けることを表します。

今回はSARIMAモデルを使って分析を行っていきます。

「7.季節調整の利用」で取得したデータのグラフを再度見てみましょう。

取得したデータは原系、トレンド、季節性、残差です。トレンドと季節性があるデータはSARIMAモデルで表現することができます。

5.パラメーターの決定

パラメーター、(p, d, q) (sp, sd, sq, s)を自動で適切にしてくれる機能はありません。
そのため 情報量規準 (今回の場合は BIC(ベイズ情報量基準) )によってどの値が最も適切なのか調べるプログラムを書かなければなりません。
そこで情報量規準 (今回の場合は BIC(ベイズ情報量基準) )によってどの値が最も適切なのか調べるプログラムを書かなければなりません。情報量規準については今回は深く触れませんが、BICの場合は この値が低ければ低いほどパラメーターの値は適切である と理解しておいてください。

ベイズコード

def selectparameter(DATA,s):
   p = d = q = range(0, 1)
   pdq = list(itertools.product(p, d, q))
   seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
   parameters = []
   BICs = np.array([])
   for param in pdq:
       for param_seasonal in seasonal_pdq:
           try:
               mod = sm.tsa.statespace.SARIMAX(DATA,
                                           order=param,
               seasonal_order=param_seasonal)
               results = mod.fit()
               parameters.append([param, param_seasonal, results.bic])
               BICs = np.append(y,results.bic)
           except:
               continue
   return print(parameters[np.argmin(BICs)])

出力結果
[(0, 1, 0), (0, 1, 0, 12), nan]

最適な(p,d,q),(sp,sd,sq,s)(p,d,q),(sp,sd,sq,s)が分かったらいよいよモデルを構築します。モデルの構築にはsm.tsa.statespace.SARIMAX(DATA,order=(p, d, q),seasonal_order=(sp, sd, sq, s)).fit()を用います。

#SARIMAモデル
SARIMA_base_df_sales = sm.tsa.statespace.SARIMAX(base_df ,order=(0,1,0),seasonal_order=(0, 1, 0, 12)).fit()
print(SARIMA_base_df_sales.bic)

6700.186496363483

予測の実行と予測データの可視化

pred = SARIMA_base_df_sales.predict("2015-01-01", "2023-12-01")
plt.plot(base_df)
plt.plot(pred, color="r")
plt.show()

次は予測データだけを出力するのではなく、もとの時系列データと予測データを同時に出力して比べてみます。赤色が予測。

実際の数字に沿ったあまり外れのない予測モデルになっているのではないかと思います。
2020年からのコロナの影響で売上が減少した後、やや微増の売上予測が見て取れます。

コロナがなかった場合の売上予測

モデルができたところで、
このモデルを使って、コロナがなかった場合の売上を予測してみます。
日本の緊急事態宣言が発令されたのは、2020年3月でしたので、
原系列のデータ期間を2020年2月までにし、コロナの影響を除去します。
（元のデータは2021年9月まで）

青が実売上
赤が1997-04-01〜2021-09-01 までのデータを読み込ませ予測したもの
　　　　　　　　　　　　　　　　　　　　　　　　　（コロナあり）
緑が1997-04-01〜2020-02-01までのデータを読み込ませ予測したもの
　　　　　　　　　　　　　　　　　　　　　　　　　（コロナなし）

以下グラフとコード

base_df2= base_df["1997-4": "2020-2"]
SARIMA_base_df_sales = sm.tsa.statespace.SARIMAX(base_df ,order=(0,1,0),seasonal_order=(0, 1, 0, 12)).fit()
SARIMA_base_df2_sales = sm.tsa.statespace.SARIMAX(base_df2 ,order=(0,1,0),seasonal_order=(0, 1, 0, 12)).fit()
pred = SARIMA_base_df_sales.predict("2015-01-01", "2023-12-01")
pred2 = SARIMA_base_df2_sales.predict("2015-01-01", "2023-12-01")
# preadデータともとの時系列データの可視化
plt.plot(base_df)
plt.plot(pred, color= "r")
plt.plot(pred2, color="g")
plt.show()

コロナ自粛による売上の差が見て取れます。

corona_pred = pred["2020-2" : "2023-1"]
nocorona_pred = pred2["2020-2" : "2023-1"]
cp_df = pd.concat([corona_pred, nocorona_pred], axis=1)
cp_df.columns = ['コロナあり', 'コロナなし']
a = corona_pred.sum()
b = nocorona_pred.sum()
c = corona_pred.mean()
d = nocorona_pred.mean()
print(c, d)
print(d - c)
print(b - a)

上記のコードから緊急事態宣言が始まった2020年３月からのコロナあり、コロナなしの売上予測を比較してみると、

2020.3〜2023.1
総売上 コロナなし・あり予測の差　　　                 　　3521868百万円
コロナなしの１ヶ月売上の平均額予測　　                      1077263百万円
コロナありの１ヶ月売上の平均額予測　                          979433百万円
コロナなし・ありの１ヶ月売上平均額予測の差  　　　100624百万円

上記の数字から
2020.3〜2023.1の総売上で、約３兆５０００億の売上の損失
2020.3〜2023.1の１ヶ月売上の平均で約１０００億の損失
が見て取れます。

１ヶ月の売上平均が大体１兆円なので3.5ヶ月分の売上が損失していると予想されます。閉店措置がなかったコンビニ業界でさえこの売上損失かと、コロナによる経済損失を改めて思い知らされます。


おわりに
今回はコンビニの売上データで時系列分析を行いましたが、理解がすすむとともにより学習を深めたくなりました。データの作成にあたって多くのサイトを参考にさせて頂きましたが、本当に勉強になることばかりでモチベーションが上がります。
このような初歩の内容だけでなく、今後も分析のための手数、手法をより学んでいきたいと思います。

最後までお読み頂きありがとうございました。