京都大学2020 文系数学 大問2 二次関数・図形と方程式

お世話になります。ドリームラーナーズの石原です。鳥取県倉吉市で進路指導と学習法指導の塾を運営しています。学習指導は中学生・高校生・大人、英語の指導は小学生から対応しています。LINEなどを活用して、遠隔地でも進路指導・学習指導に対応しています。

今日は過去問解説にチャレンジします。京都大学の文系数学の大問２です。問題本体は載せませんので、ご自分で用意してください。

なるべく「与えられた問題文をどう読むか、読んで何を考えるか」と言う点を重点的に解説していきたいと思います。あと、「いかに簡単に、楽して解くか」も重視します。数式を試行錯誤してぐちゃぐちゃやって解けた、と言う話はあまり参考にならないと思いますし、時間内に解ききれません。載せているのは考え方だけです。私が普段やっている指導では、これを小出しにしながら誘導していくスタイルを取っています。

大問２：とりあえず与えられた条件を羅列しよう

問題自体は短いです。

なので、とりあえず

ぐらいはすぐ書こうと思いつくでしょう。

大問２：交点の評価

2交点は、f(x)も通るので、

となります。整理すると

こうなりますが、この２式をみてs,tの対称性から気付かなければいけないことがあります。つまり、

と言えるのです。とりあえず、aは1ではないなど思いつくと思いますが、深追いしすぎず、次の評価に移りましょう。

大問２：交点での傾きの評価

そして、今度は交点の傾きについて考えます。２図形が直交するので、

となり、整理すると

これも同様に、

と判断できます。

大問２：同じ２実数解をもつ別々の実係数二次方程式

同じs,tを解にもつ、実係数二次方程式である①の二式は同一のものであると考えることができます。係数比較の出番ですが、どこから手をつけましょう。

xの係数が、bと2bなので比を使えそうですが、bがゼロだと台無しなのでそこで場合分けできそうです。まずbがゼロでないとき、

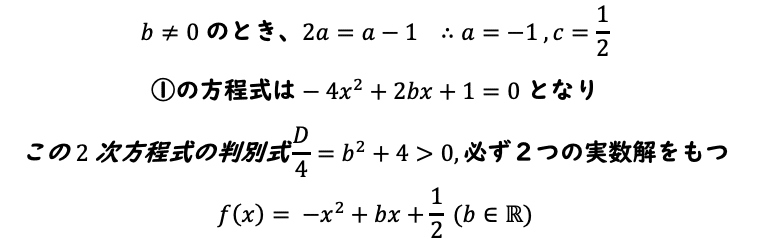
次にb=0のとき、係数比が一致することを利用して、

以上より、

ともとまりました。

本日は以上です。

難関大志望者の中で勝ち残る学習法を公式ウェブサイトで公開中！
LINEやSkypeによる無料相談も受付中！

【初回相談無料】ドリームラーナーズ