東京大学2020文科 数学 大問２ 場合の数

お世話になります。ドリームラーナーズの石原です。鳥取県倉吉市で進路指導と学習法指導の塾を運営しています。学習指導は中学生・高校生・大人、英語の指導は小学生から対応しています。LINEなどを活用して、遠隔地でも進路指導・学習指導に対応しています。

今日は過去問解説にチャレンジします。東京大学文科の数学です。問題本体は載せませんので、ご自分で用意してください。

なるべく「与えられた問題文をどう読むか、読んで何を考えるか」と言う点を重点的に解説していきたいと思います。あと、「いかに簡単に、楽して解くか」も重視します。数式を試行錯誤してぐちゃぐちゃやって解けた、と言う話はあまり参考にならないと思いますし、時間内に解ききれません。載せているのは考え方だけです。私が普段やっている指導では、これを小出しにしながら誘導していくスタイルを取っています。

大問２：状況整理

この問題、結局、下図のように、縦横４本ずつ等間隔で並んだ線分で作られる、16個の点のうち5個を選んで置いていく、という状況ですよね。

（１）では、この８本の線分のうち、２本に全く点が配置されない状況

（２）では、この８本全てに少なくとも１つの点が配置されている状況

これらの場合の数を求めていく、というわけです。

例えば、２本の線に全く点が配置されないことを考えてみると、

どの２本を、点が配置されない線として選ぶか？　選んだ線によって数え方が変わるか？　を考慮する必要がありそうですね。

また、８本全てに少なくとも１つの点が配置されるということは、どのように点を置くかが、かなり制限されそうです。それが、どのように制限されるかを考えてく必要がありそうですね。

大問２（１）：２本に点が配置されない状況の場合の数

状況整理で考えたように、まずどの２本に点が配置されないかを考えてみます。とはいえ８本しかないですし、横と縦にきれいに別れてますから、次のように場合わけしてみましょう。

①縦の線を２本選ぶ場合
この場合、どの２本を選んでも、残りの置ける点は8個になります。

②横の線を２本選ぶ場合
これは対称性から、縦の線を２本選ぶ場合と変わらないですね。

③縦と横と１本ずつ選ぶ場合
この場合、どの線を選んでも、残りの置ける点は9個になります。

以上から、場合わけは

①縦あるいは横で２本点が配置されない場合
②縦と横で１本ずつ点が配置されない場合

の２通りを数えれば良さそうですね。

大問２（１）：同方向２本に配置されない場合

上図を再掲します（縦２本の場合）。

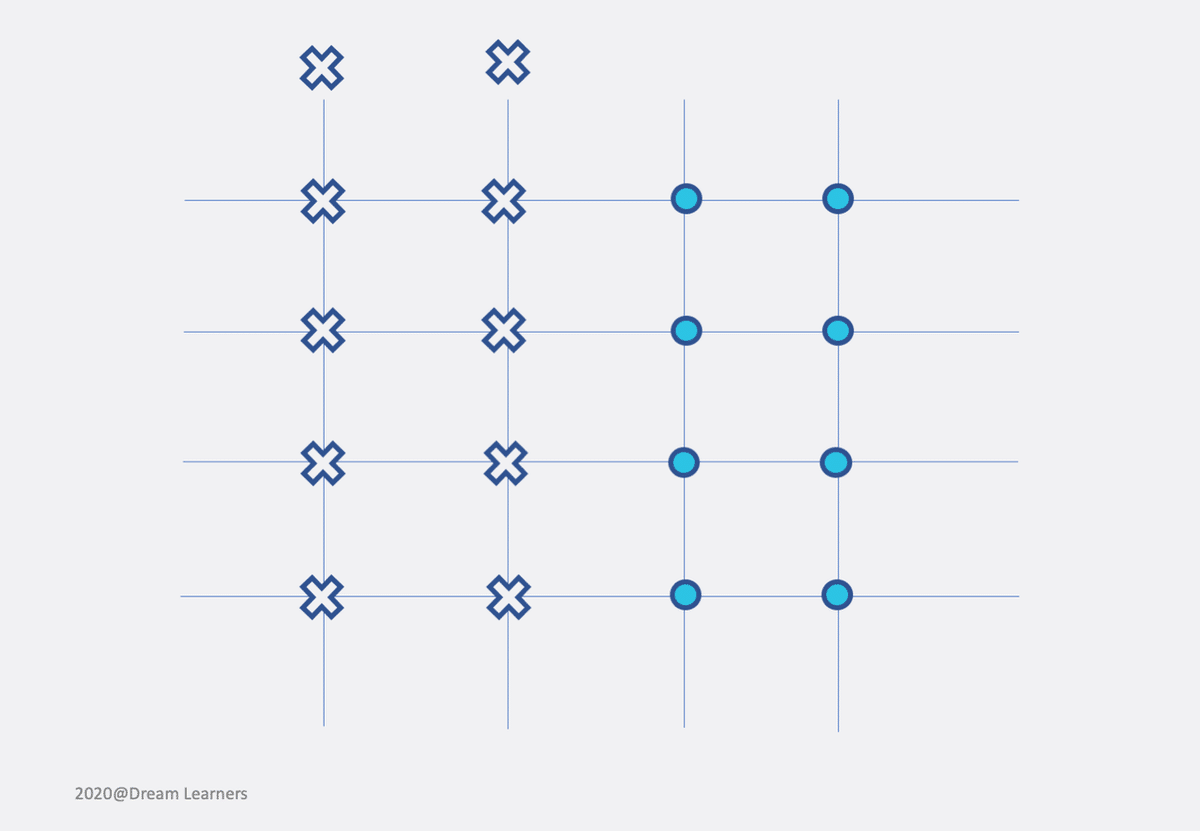
さてこれで、「残りの線に全て点が配置される場合の数」を数えれば良いわけですが、どう数えるかはいくつかやり方がありますが、いずれにせよこれ以上点が配置されない線が増えると困るわけですから、まず配置されない線が出てしまう場合の数を数えてみます。

①縦がもう一本、配置されない…のは、なさそうですね。配置できる点が残り4個になってしまうので、点を5つ選べません。

ということで、②横がもう一本配置されない、だと、配置できる点が残り6個となり、これ以降はどう置いても点が配置されない線は出ません。ここから５つを選んで点を配置するので、場合の数は６通りです。

ということは、選ばれない線を決める４通りに対してそれぞれ６通りの場合の数が対応しますから、それらを取り除いてやる必要があります。

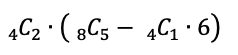
そしてこれらは、対称性から、横を２本選んでも同じ場合の数になるので、全体を２倍した以下の場合の数になります。

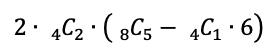
まとめると、このような数え方をしました。

大問２（１）：縦と横１本ずつに配置されない場合

図を再掲します。

残り9個の点に5個配置するわけですが、縦横２本ずつの場合と同じように、これ以上点が配置されない線が増えると困ると考えて、まず配置されない線が出てしまう場合の数を数えてみます。

配置されない追加の１本を決めたあとの場合の数は、縦横どれに決めようが、残り6個となりますので、６通りです。念のため図を再掲します。

ということで、

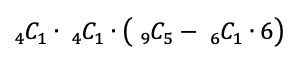
こうなります。式の意味はこうです。

以上の２つの場合の数を合わせて、

似たような整数の積がいっぱいある場合には、くくりながら（因数分解しながら）計算を進めてミスを減らしましょう。

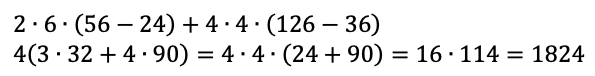
大問２（２）：全ての線に少なくとも1個配置される場合

横の線だけに注目すると、全ての線に少なくとも1個配置されるときには、

いずれか１本に２個、他の３本に1個ずつ配置される

ことになります。で、これは縦の線に注目する場合も同じです。

ということは、

2個配置される線が縦と横に１本ずつある

ということになります。では、これを１本ずつ選んだ場合に、置き方がどのように変わるかを見ていきましょう。

この２本の線に、２つ配置するとします。置き方が明らかに変わるのは、２つの線の交点部分に点を配置する場合と、しない場合、です。

①配置する場合

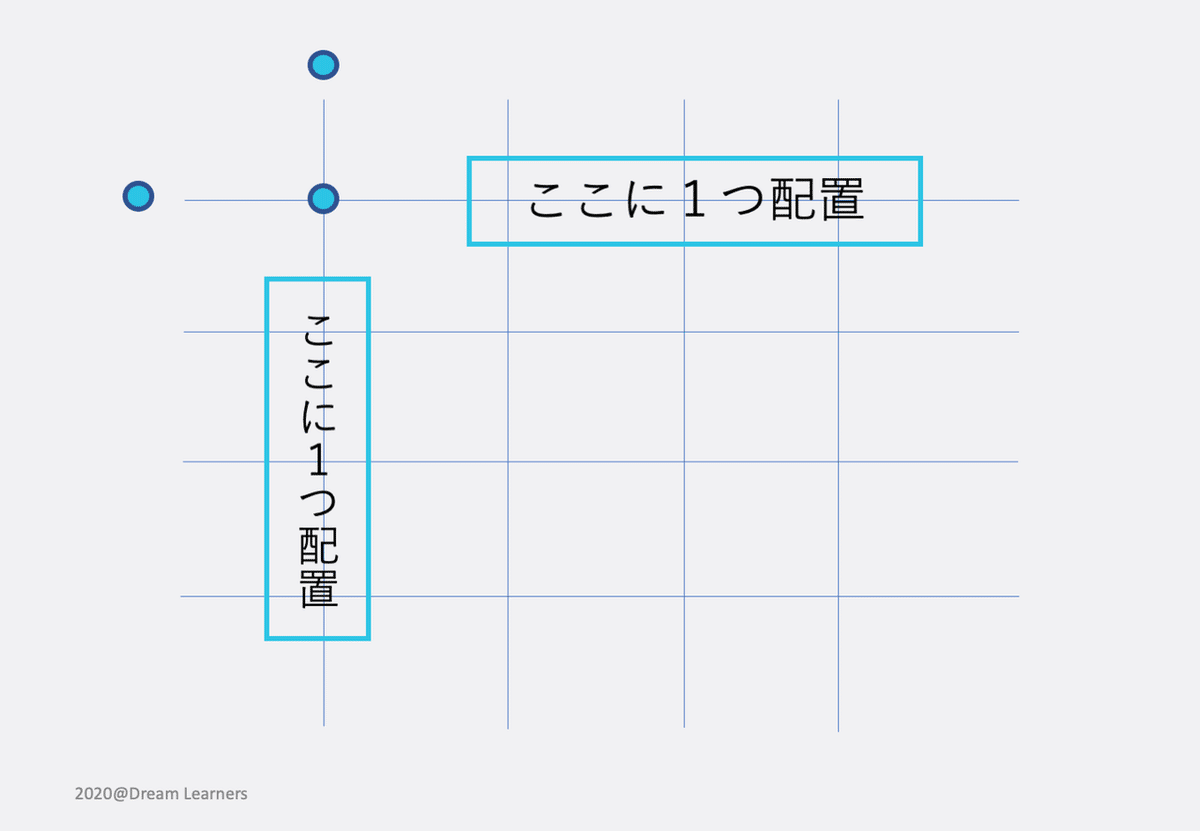
この置き方になります。仮に、１つずつ配置した場合、残り配置できる点は４カ所から選べるのですが、

無配置の線が４本に対して、点は残り２つしか置けず、これ以上１つの線に２つの点は配置できないため、取りうる場合の数は、２通りだけになります。

まとめると、

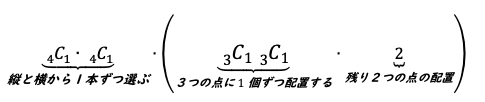
となります。

②配置しない場合

となります。２つずつ配置したら、以下のように、置ける点は１つになりますので、残る１個の点の配置はそこで決まります。

まとめると、

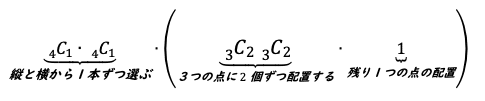
となります。

２つの場合の数を合わせて、

となります。

難易度は例年並みでしょう。見抜くまでに時間がかかりそうですが、大問４ほどではないと思います。

本日は以上です。

難関大志望者の中で勝ち残る学習法を公式ウェブサイトで公開中！
LINEやSkypeによる無料相談も受付中！

【初回相談無料】ドリームラーナーズ