慶應義塾大学2020商学部 数学 大問２ 確率

お世話になります。ドリームラーナーズの石原です。鳥取県倉吉市で進路指導と学習法指導の塾を運営しています。学習指導は中学生・高校生・大人、英語の指導は小学生から対応しています。LINEなどを活用して、遠隔地でも進路指導・学習指導に対応しています。

今日は過去問解説にチャレンジします。慶應義塾大学商学部の数学です。問題本体は載せませんので、ご自分で用意してください。

なるべく「与えられた問題文をどう読むか、読んで何を考えるか」と言う点を重点的に解説していきたいと思います。あと、「いかに簡単に、楽して解くか」も重視します。数式を試行錯誤してぐちゃぐちゃやって解けた、と言う話はあまり参考にならないと思いますし。載せているのは考え方だけです。私が普段やっている指導では、これを小出しにしながら誘導していくスタイルを取っています。

多分、クソ真面目に全部やりがちで遅くて間に合わねえ！もっと時間かけたい問題に時間かけられねえじゃねえか！という人にはうってつけの解説かと思います。

大問２：状況把握

難関大学で出てくる確率の問題では「状態遷移」を考えるとうまくいくことが多いです。この問題でも、２つの動点の「距離」だけに注目すると、何が起これば目標の現象に到達するのかが見やすくなります。

動点は必ず動くので、２つの動点の距離は「２つ分縮む」「変わらない」「２つ分離れる」の３種類の遷移のみをします。そして、一度「一致」してしまった動点はその後離れることはありません。

そして、３つの動点はお互いに「偶数個分」の距離しか離れていませんし、最大でも4個分しか離れません。

問題文では角度π/4で示されていますが、面倒なので「○個」で表現します。

なので、距離は４、２、ゼロの３通りで、コインの裏表によりこの状態を移動したりしなかったりします。この状態遷移を図示するとこうなります。

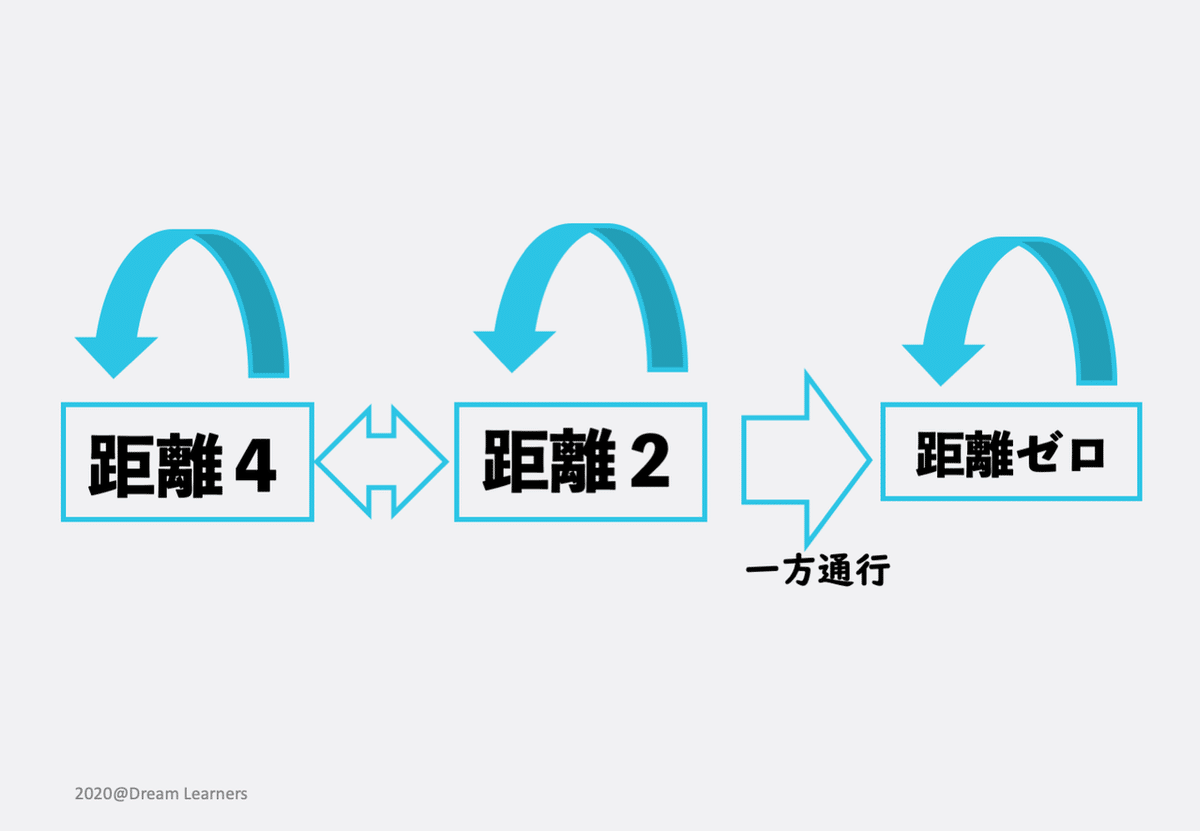
２つの動点に関係するコインだけが、移動に関わってくるので、それ以外のコインは何が出ようが関係ありません。で、移動に関わるコインは動点の位置で決まるので、場合の数などを考える上で、どのコインの裏表を吟味する必要があるか、考察しなくて良いです。

なので、移動に関わってくるのは、２枚のコイン、その２つの裏表だけを考えれば良いのです。

２つの動点の動きを示すコインが、「両方表」や「両方裏」なら同じ方向に移動するので、距離は「変わらない」です。

距離４or距離２で距離が変わらない：両方表or両方裏、1/2

距離４→距離２の移動：表裏が異なれば移動するので、1/2

距離２→距離４の移動：裏表が異なるうちのどちらか一方なので、1/4

距離２→距離ゼロの移動：表裏が異なるうちのどちらか一方なので、1/4

以上を図に書き込むとこうなります。

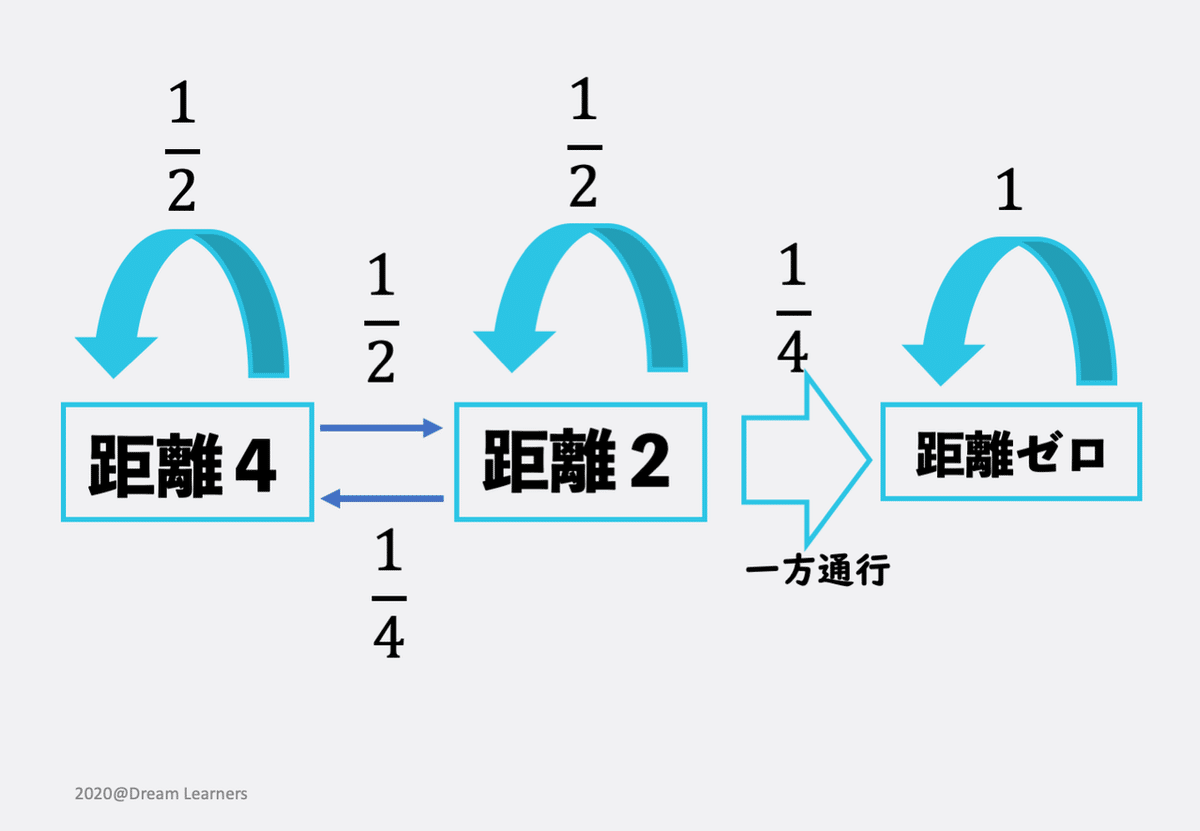
はい、ここまで状況把握が終われば、あとは計算するだけになります。

大問２：（ⅰ）試行Tを２回行う

AとBが一致：

AとBは初期状態で距離２なので、
１回目で一致：1/4
２回目で一致：距離２→距離２→距離ゼロの移動なので、(1/2)*(1/4) =1/8
２つの確率は同時に起こらないので、これを足して3/8

AとCが一致：

AとCは初期状態で距離４なので、
１回目で一致：ありえない
２回目で一致：距離４→距離２→距離ゼロの移動なので、(1/2)*(1/4)=1/8
よって、1/8

AとBとCが一致：

AとCが距離４→距離２→距離ゼロと詰めていく間に必ずBはAまたはCのどちらかと一致する。１回目だけは動点が３つあるので状態遷移ではなく、それぞれの動点がどのように移動するかが、制限が強いので直接考える。

BがAと一致する場合、BがCと一致する場合、
どちらでも２回目は、動点が２つしかないので、距離２→距離ゼロで1/4。

BがAと一致する場合の１回目：A左、B右、C右、なので1/8
BがCと一致する場合の１回目：A左、B左、C右、なので1/8

よって、(1/8 + 1/8)*1/4 = 1/16

大問２：（ⅱ）試行Tを２回行う＋条件付き確率

AとBの座標が一致している、という条件でのCの座標がAとBの座標と一致している確率。（ⅰ）からスルッと導ける。

分母：3/8（AとBが一致）
分子：1/16（AとBとCが一致）
なので、1/6

大問２：（ⅲ）試行Tを４回行う

AとCが一致している：（"距離"記載は省略）

２回目で初めて一致

→２→ゼロ：1/8

３回目で初めて一致

→４→２→ゼロ：1/16
→２→２→ゼロ：1/16

４回目で初めて一致

→２→２→２→ゼロ：1/32
→２→４→２→ゼロ：1/64 ←これ忘れがち
→４→２→２→ゼロ：1/32
→４→４→２→ゼロ：1/32

以上を足して、(8+8+7)/64 = 23/64

大問２：（ⅳ）試行Tを５回行う

５回目で初めて一致する場合だけ考えて（ⅲ）の答えに足せば良い。

→４→…１回目で距離が変わらない場合は、
残り４回で初めて一致すれば良いので、(1/2)*(7/64)

→２→４→…残り３回で初めて一致、(1/8)*(1/8)=1/64

→２→２→４→…残り２回で初めて一致、(1/16)*(1/8)

→２→２→２→２→０ 1/64

以上より、５回目で初めて一致する確率は、(7+2+1+2)/128 = 6/64
ちなみにどうせ足すとわかっているんだから分母は64で止めとくと無駄な計算せずに済見ます。

足して、29/64

本日は以上です。

難関大志望者の中で勝ち残る学習法を公式ウェブサイトで公開中！
LINEやSkypeによる無料相談も受付中！

【初回相談無料】ドリームラーナーズ